
Министерство образования и науки Краснодарского края
Государственное бюджетное профессиональное образовательное учреждение
Краснодарского края
«Армавирский механико – технологический техникум»
Методическое пособие
для проведения
практического занятия
на тему:
«ПОСТРОЕНИЕ ЭПЮР ПОПЕРЕЧНЫХ СИЛ И ИЗГИБАЮЩИХ МОМЕНТОВ»
по дисциплине: «Техническая механика»
для студентов 2 курса
15.02.05
Разработал преподаватель: Е.В. Игнатова
|
|
|
2016
1 ЦЕЛЬ РАБОТЫ
Знать:
- знать порядок построения и контроля эпюр поперечных сил и изгибающих моментов;
Уметь:
-строить эпюры поперечных сил и изгибающих моментов.
2 ДЛЯ ЗАЧЕТА РАБОТЫ НЕОБХОДИМО:
- изучить теоретический материал с помощью методического пособия;
- по варианту задания выполнить расчеты и построить эпюры поперечных сил и изгибающих моментов;
- ответить на контрольные вопросы.
3 КРАТКОЕ ИЗЛОЖЕНИЕ ТЕОРЕТИЧЕСКОГО МАТЕРИАЛА
3.1 Основные положения
Изгибом называется такой вид нагружения, при котором в поперечном сечении бруса возникает внутренний силовой фактор – изгибающий момент. Брус, работающий на изгиб, называется балкой.
Изгиб, при котором в поперечном сечении бруса возникает только изгибающий момент, называется чистым изгибом.
Изгиб, при котором в поперечном сечении бруса возникает изгибающий момент и поперечная сила, называется поперечным изгибом.
Эпюры поперечных сил и изгибающих моментов можно строить, предварительно разделив балку на участки нагружения и составляя уравнения, выражающие изменения Q и Мх по участкам.
Границы участков нагружения – это сечения, в которых приложены внешние нагрузки.
3.2 Принятые в машиностроении знаки поперечных сил и изгибающих моментов
Поперечная сила в сечении считается положительной, если она стремится развернуть сечение по часовой стрелке (чертеж 1а), если против часовой стрелки, — отрицательной (чертеж 2б).
Знаки поперечных сил
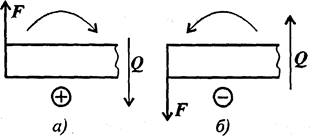
Чертеж 1
Если действующие на участке внешние силы стремятся изогнуть балку выпуклостью вниз, то изгибающий момент считается положительным (чертеж 2а), если наоборот — отрицательным (чертеж 2б).
Знаки изгибающих моментов

Чертеж 2
4 ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАНИЯ
На балку действуют сосредоточенные силы и момент (чертеж 3). Построить эпюры поперечных сил и изгибающих моментов.
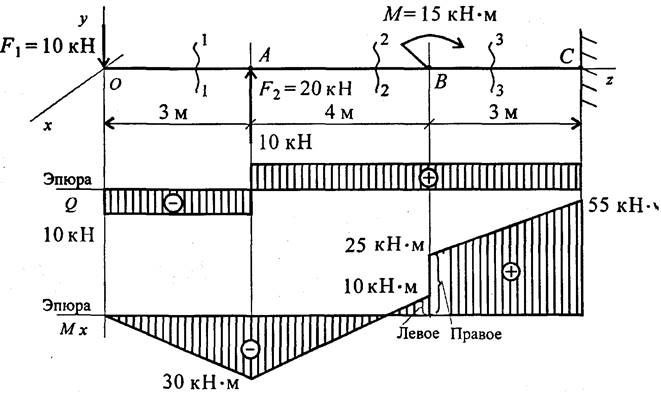
Чертеж 3
Решение:
Последовательно по участкам нагружения рассмотреть внутренние силовые факторы в сечениях. Силовые факторы определить из условий равновесия отсеченной части. Для каждого участка записать уравнения внутренних силовых факторов.
Использовать известные правила:
— поперечная сила численно равна алгебраической сумме проекций внешних сил на ось Оу;
— изгибающий момент численно равен алгебраической сумме моментов внешних сил, действующих на отсеченную часть, относительно нейтральной оси, совпадающей с осью Ох;
Составить уравнения равновесия.
1. Рассмотреть участок 1 (чертеж 3).
∑y=0;
Q y1= -F1= -10 кН
Сила Q y1 — отрицательна. Сила Q на участке 1 постоянна.
∑mx1=0;
-F1z1 + Мх1=0
Мх1= F1z1 Мх— отрицательный
0 ≤ z1≤3 м:
при z1= 0; Мхо =0;
при z1=3м; МхА =-30кН.
Изгибающий момент меняется по линейному закону, график - прямая линия.
2. Рассмотреть участок 2 (чертеж 3).
∑ Fy=0;
Q y2= -F1 + F2;
Q y2 = -10 + 20 = 10кН.
Сила Q y2 положительна.
∑mx2=0;
-F1z2 + F2 (z2 - 3)+ Мх2=0
Мx 2= F1z2 - F2 (z2 - 3)
3 м ≤ z2 ≤ 7 м:
при z2 = 3 м
МхА = 10∙3 = 30 кН∙м; Мх — отрицательный;
при z2 = 7м
МхВслева =10∙7 - 20∙4 = -10 кН∙м
Знак сменился; МХв слева от сечения В — положительный.
Поперечную силу и изгибающий момент можно определять сразу из зависимостей Q y=∑ Fy; Мх=∑mx не составлял уравнения равновесия участка.
Знак каждого из слагаемых этих уравнений определить отдельно (участок 3).
3. Рассмотреть участок 3 (чертеж 3).
Q y3 = -10 + 20 = 10 кН — положительна.
тхз = 0;
Мx3= -Fz3 + F2 (z3 - 3) + m
7м ≤ z3 ≤ 10м:
при z3= 7 м
МхВсправа = -10∙7+20∙4+15 = 25 кН∙м;
при z3 = 10 м.
Мхс = -10∙10 + 20∙10 + 15 = 55 кН∙м.
Для точки В получено два значения изгибающих моментов: из уравнения для участка 2 левее точки В из уравнения для участка 3 — правее точки В.
Это объясняется тем, что именно в этой точке приложен внешний момент и поэтому внутренний момент сил упругости меняется.
В точках приложения внешнего момента на эпюре моментов появится скачок, равный величине приложенного момента.
Поперечная сила в точке В для второго и третьего участков одинакова. Следовательно, приложение внешнего момента не отражается на эпюре поперечных сил. График поперечной силы на участке 3 — прямая линия.
График изменения изгибающих моментов на третьем участке также прямая линия.
4. Построение эпюр. Порядок построения эпюр остается прежним: масштабы эпюр выбираются отдельно, исходя из значений максимальных сил и моментов.
Графики обводятся толстой основной линией и заштриховываются поперек. На графиках указываются значения поперечных сил, изгибающих моментов и единицы измерения.
5 ЗАДАНИЕ
Для одноопорной балки, нагруженной сосредоточенными силами и парой сил с моментом т, построить эпюры поперечных сил и изгибающих моментов.
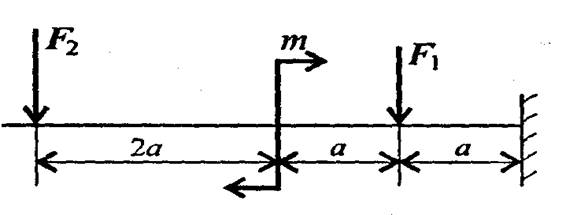
Рисунок 1

Рисунок 2
ВАРИАНТЫ ЗАДАНИЙ
|
Вариант |
Рисунок |
F1, кН |
F2, кН |
m, кН м |
а, м |
|
1 |
1 |
10 |
4,4 |
8 |
0,2 |
|
2 |
1 |
12 |
4,8 |
7 |
0,2 |
|
3 |
1 |
14 |
7,8 |
6 |
0,3 |
|
4 |
1 |
16 |
8,4 |
5 |
0,3 |
|
5 |
1 |
18 |
12 |
4 |
0,4 |
|
6 |
1 |
10 |
12,8 |
8 |
0,4 |
|
7 |
1 |
22 |
17 |
7 |
0,5 |
|
8 |
1 |
24 |
18 |
6 |
0,5 |
|
9 |
1 |
26 |
22,8 |
5 |
0,6 |
|
10 |
1 |
28 |
24 |
4 |
0,6 |
|
11 |
2 |
12 |
6,4 |
10 |
0,4 |
|
12 |
2 |
14 |
6,8 |
9 |
0,4 |
|
13 |
2 |
16 |
9,8 |
8 |
0,5 |
|
14 |
2 |
18 |
10 |
7 |
0,5 |
|
15 |
2 |
20 |
14 |
6 |
0,6 |
|
16 |
2 |
12 |
15 |
10 |
0,6 |
|
17 |
2 |
24 |
20 |
9 |
0,7 |
|
18 |
2 |
26 |
25 |
8 |
0,7 |
|
19 |
2 |
28 |
24 |
7 |
0,8 |
|
20 |
2 |
30 |
26 |
6 |
0,9 |
|
21 |
3 |
8 |
2,4 |
6 |
0,1 |
|
22 |
3 |
10 |
2,8 |
5 |
0,1 |
|
23 |
3 |
12 |
5,8 |
4 |
0,2 |
|
24 |
3 |
14 |
6,4 |
3 |
0,2 |
|
25 |
3 |
16 |
10 |
2 |
0,3 |
|
26 |
3 |
8 |
11 |
6 |
0,3 |
|
27 |
3 |
20 |
15 |
5 |
0,4 |
|
28 |
3 |
22 |
16 |
4 |
0,4 |
|
29 |
3 |
24 |
21 |
3 |
0,5 |
|
30 |
3 |
26 |
22 |
2 |
0,6 |
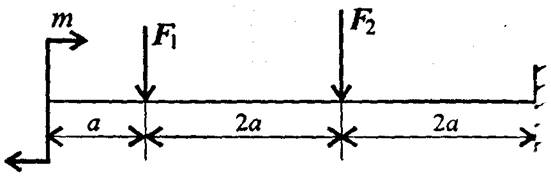
Рисунок 3
6 КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что такое изгиб?
2. Когда поперечная сила считается положительной?
3. Какими линиями очерчены эпюры поперечных сил?
4. Указать единицу измерения изгибающего момента.
5. Когда изгибающий момент считается отрицательным?
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.