
ПЗ № 14.1. Нахождение значений логарифма по произвольному основанию. Переход от одного основания к другому.
Задание:
1)Перепишите:
1.Вычислим пример по
формуле ![]()
![]()
2. Вычислим пример
по формуле ![]()
![]()
3. Вычислим пример
по формуле ![]()
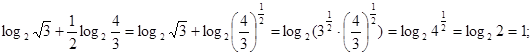
4.Вычислим пример по
формуле ![]()
![]()
5.Найдите значение выражения: ![]()
6. Найдите значение выражения: ![]()
7. Найдите значение
выражения:
![]()
8.
Найдите значение выражения: 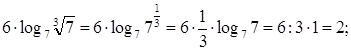
9. Найдите значение выражения:
![]()
10. Найдите значение выражения: ![]()
11. Найдите значение выражения: ![]()
12. Найдите значение выражения: ![]()
13. Найдите значение выражения: ![]()
14. Найдите значение выражения: ![]()
15. Найдите значение выражения: ![]() .
.
16. Найдите ![]() , если
, если ![]()
![]()
2) Перепишите и заполните пропуски:
1)![]() 2)
2) ![]() 3)
3)
![]()
4) ![]() 5)
5) ![]() 6)
6) ![]() 7)
7)
![]()
8) ![]() 9)
9) ![]() 10)
10)
![]()
11) ![]() 12)
12) ![]()
13) ![]()
14) ![]()
15) ![]() 16)
16) 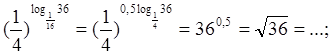
17) ![]() 18)
18) ![]()
19) ![]()
20) ![]()
21) ![]()
22) ![]()
23) ![]()
24) ![]()
25) ![]() 26)
26) ![]()
27) ![]()
28) 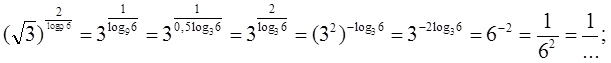
![]()
![]() 30)
30)![]()
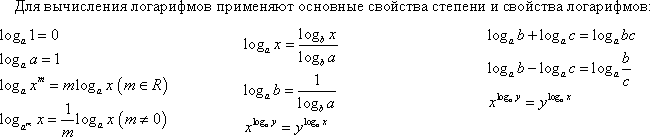
3)Решить задание :Найдите значение выражения:
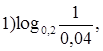
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
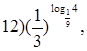
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
ПЗ № 14.2. Вычисление и сравнение логарифмов. Логарифмирование и потенцирование выражений. Приближенные вычисления и решения прикладных задач.
Задание:
1) Перепишите и заполните пропуски:
Пример 1. log3 9 = 2, так как 32
= 9, log5 25 = 2, так как 52
= 25, log3 81 = 4, так как 34
= 81,
Ответ: 2,2,4.
Пример 2. Вычислите : а) log2 16, б) log3 3, в) ![]() , г)
, г) ![]() , д) log2 2 log3 81, е) log12 2 + log12 72, ж) log5 75 – log5 3.
, д) log2 2 log3 81, е) log12 2 + log12 72, ж) log5 75 – log5 3.
Решение: а) log2 16 = 4, б)
log3 3 = …, в) ![]() = 16, г)
= 16, г) ![]() =
= ![]() =
…,
=
…,
д) log2 2 log3 81= 1· 4 = …, е) log12 2 + log12 72 = log12 (2 ·72) = log12 144 = …,
ж) log5 75 – log5 3= log5 (75:3) = log5 25 = …
Ответ: а) 4, б) 1, в) 16, г) 8, д) 4, е) 2, ж) 2.
Пример 3. Найдите х, если logx 36 = 2 и log2 x = – 2.
Решение: logx 36 = 2, х2
= 36, х = ![]() log2 x = - 2, х = 2 -2
= 1 / 4 = …
log2 x = - 2, х = 2 -2
= 1 / 4 = …
Ответ:
![]() 0,25
0,25
Пример
4.
Вычислите:
а) ![]() , б)
, б) ![]() , в)
, в) ![]() .
.
Решение: а) ![]() = – log2 16=…, б)
= – log2 16=…, б) ![]() = 5 ·
= 5 · ![]() =
5 · 3
= … ,
=
5 · 3
= … ,
в) ![]() =
= ![]()
![]() =
= ![]() 17
= 1296 – 17 = …
17
= 1296 – 17 = …
Ответ: – 4, 15, 1279.
Пример 5. Упростите выражение :
а) ![]()
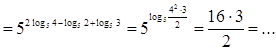 ;
;
б)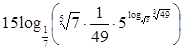
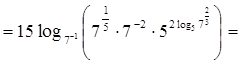
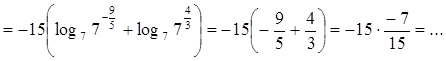 ;
;
в) ![]()
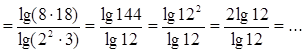 ;
;
Ответ: 24, 7, 2.
2) Опорный конспект.
Вспомним основные приемы сравнения положительных чисел а и b.
1) Составить разность a-b и сравнить ее с нулем.
2) Составить частное a:b и сравнить его с единицей.
Свойства логарифмической функции или свойства логарифмов чисел применяются при сравнении логарифмов чисел:
Монотонность логарифмической фунции; Свойства: 0 <X1 <X2
loga X1 < loga X2, если a >1
loga X1 > loga X2, если 0 < а < 1
Пример
1. Сравнить
![]() и
и ![]() ,
, ![]()
a = 15 >1, ![]() >
>![]() .
.
Пример
2. Сравнить ![]() и
и ![]() ,
, ![]()
знак
меняется , ![]() <
< ![]()
Пример
3. Сравнить
![]() и
и ![]() .
.
Решение:
![]()
значит, ![]() значит,
значит, ![]()
Известными способами сравнить можно не все числа. Рассмотрим следующий пример. Основания разные, логарифмируемые числа разные. Также, как и при сравнении иррациональных чисел, применяется метод «оценки» или сравнение с каким-нибудь «хорошим» числом.
Пример 4.
Сравнить ![]() и
и ![]() .
.
![]() ,
а
,
а![]() , значит,
, значит, ![]()
![]() .
.
Пример
5. Сравнить ![]() и
и ![]() .
.
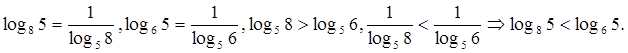
Основное логарифмическое тождество
![]() ,
, ![]()
Логарифм произведения — это сумма логарифмов
![]() ,
, ![]()
Логарифм частного — это разность логарифмов
![]() ,
,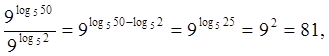
Свойства степени логарифмируемого числа и основания логарифма
Показатель
степени логарифмируемого числа ![]()
Показатель
степени основания логарифма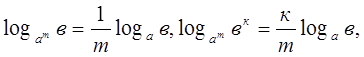 ,
,
в
частности если m = n, мы получаем формулу: ![]() ,
,
например: ![]()
Переход
к новому основанию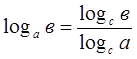 , частности, если c = b, то
, частности, если c = b, то ![]() , и тогда:
, и тогда: 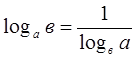 .
.
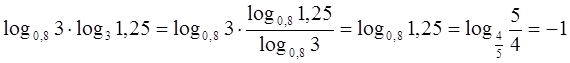
Логарифмирование – это нахождение логарифмов заданных чисел или выражений.
b
Пример: Найдем логарифм x = a2 · — .
c
Решение.
Последовательно
воспользуемся сразу всеми тремя основными свойствами логарифмов, которые
изложены выше (логарифм произведения, логарифм частного и логарифм степени):
b
lg x = lg (a2 · —) = lg a2 + lg b – lg c = 2lg a + lg b – lg c.
c
Потенцирование – это нахождение чисел или выражений по данному логарифму числа (выражения).
Потенцировать – значит освобождаться от значков логарифмов в процессе решения логарифмического выражения.
Пример: ![]() Ответ:
Ответ: ![]()
Десятичный логарифм — логарифм с основанием 10, который обозначается как lg.
lg100=2log10100=2, так как 102=100 .
Натуральный логарифм — логарифм с основанием e, обозначается ln.

![]()
Задача 2

Задача 3
По данным газеты «Зори» от 12 апреля 2011 года из доклада П. Е.
Шишкина население в городе Старый Оскол за один год увеличилось с 256100
человек до 257135 человек. Через сколько лет население этого города увеличится
в 1,5 раза?
Решение. Для решения этой задачи применим формулу сложных
процентов: A=a(1+p/100)x. Примем население города,
которое было, за а=256100, тогда А=257135-это население,
которое стало, х -неизвестно.
р=((257135256100)/257135)100≈0,4%
Сделав подстановку в формулу, получим 256100∙1,5=256100(1+0,4/100) x
Чтобы решить это показательное уравнение прологарифмируем его.
xlg 1,004=lg1,5, откуда x =lg 1,5 /lg1,004
Найдя по таблице lg1,5 и lg1,004 , получим x=0,18/0,002≈90.
Ответ : примерно через 90 лет.
Задача 4
Высота над уровнем моря вычисляется по формуле h=(8000/0,4343)lg(p0 /p),
где p0 =760 мм рт.ст., р -
давление на высоте h м.
Давление в городе Старый Оскол на 15 апреля 2011 года равно 738 мм рт. ст.
Вычислим, на какой высоте находится наш город.
Решение. Найдем высоту, на которой находится наш город:
h=(8000/0,4343)lg(760/738) ≈235 м
Ответ: 235м.
Задача 5
В начальный момент времени было 8 бактерий. Через 2 часа после помещения бактерий в питательную среду, их число возросло до 100. Через сколько времени с момента размещения в питательную среду следует ожидать появления 500 бактерий?
Решение.
Для решения данной задачи, необходимо вспомнить понятия скорости и ускорения.
|
Было -8 Стало- 100 |
|
|
|
1 изменение: |
||
=> ![]() конечное
значение скорости распространения бактерий при первом изменении -
конечное
значение скорости распространения бактерий при первом изменении - ![]()
|
Было -8 Стало- 500 |
|
|
|
2 изменение: |
||
=> ![]() конечное
значение скорости распространения бактерий при втором изменении -
конечное
значение скорости распространения бактерий при втором изменении - ![]() .
.
Составим
формулу для ускорения, учитывая, что начальная скорость ![]() (т.е.
было -8, стало -8):
(т.е.
было -8, стало -8):
![]() =
= ![]()
![]() =
= ![]()
Т.к.
ускорение постоянно => ![]() =>
=>
![]()
Перейдем к натуральному основанию логарифмов, для того, чтобы можно было воспользоваться табличными значениями:
![]()
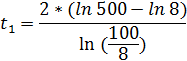
Ответ: приблизительно 3часа 15 минут.
3)А)Решить задание ( по примерам):
1. Вычислите а) log3 27, б) log4 1,в) log1/2 4,
2.
Вычислите
а) log2 32, б) log3 9, в) ![]() , г)
, г) ![]() ,
,
д) log3 3· log2 8, е) lg 5 + lg 2, ж) log3 15 – log3 5.
3. Найдите х, если log2 4 = x и log6 x = 2.
4.
Вычислить
а) ![]() б)
б) ![]()
в) ![]() .
.
5. а)
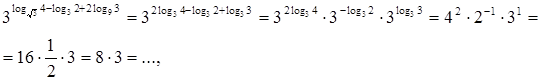
б) ![]()
в)
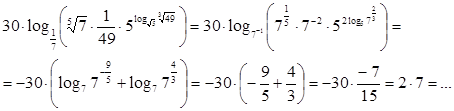
г) ![]()
д)
![]()
е) ![]()
Б) 1)log9
81 ; 2) ![]() 3) log3
1; 4) log5 5 ; 5)
3) log3
1; 4) log5 5 ; 5) ![]()
6)![]() 7) log2
log3 9; 8) lg100; 9) 92 log9 5
; 10) log64 8
7) log2
log3 9; 8) lg100; 9) 92 log9 5
; 10) log64 8
Ответы: вставьте номер задания
|
№ задания |
|
2 |
7 |
10 |
|
|
5 |
|
|
1 |
|
ответ |
2 |
4 |
1 |
0,5 |
1 |
0 |
-2 |
25 |
-1 |
2 |
В) 1.Сравнить ![]() и
и ![]() ,
,
2.
Сравнить ![]() и
и ![]()
3.
Сравнить ![]() и
и ![]() .
.
4. Прологарифмируйте по основанию 10 (a > 0,b > 0), x = a2b3.
5. Прологарифмируйте по основанию 3 (a > 0,b > 0), x = 7a3b.
6.Найдите
x, если ![]()
7. Найдите x, если ![]() .
.
С) Задания для практической работы:

1-2.
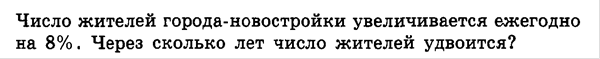
3-4.

5.Для обогрева помещения, температура в котором равна Тп = 200С, через радиатор отопления, пропускают горячую воду температурой Тв = 1000С. Расход проходящей через трубу воды m = 0,2 кг/с. Проходя по трубе расстояние x (м), вода охлаждается до температуры Т0С, при чём
![]() , где с =
4200Дж/кг*С — теплоемкость воды
, где с =
4200Дж/кг*С — теплоемкость воды
![]() = 42
Вт/м *
0С—
коэффициент теплообмена , a = 1,4 — постоянная.
= 42
Вт/м *
0С—
коэффициент теплообмена , a = 1,4 — постоянная.
До какой температуры (в градусах Цельсия) охладится вода, если длина трубы 28 м?
4)Решить задание :
1. Вычислите (по свойству степени):
1) ![]() , 2)
, 2) ![]() , 3)
, 3) ![]() , 4)
, 4) ![]() , 5)
, 5) ![]() ,
,
6) ![]() , 7)
, 7) ![]() , 8)
, 8) ![]() ,9)
,9) ![]() , 10)
, 10) ![]() , 11)
, 11) ![]() ,
,
12) ![]() , 13)
, 13) ![]() , 14)
, 14) ![]() , 15)
, 15) ![]() , 16)
, 16) ![]() .
.
2. Вычислите (по основному лог. тождеству):
1) ![]() , 2)
, 2) ![]() , 3)
, 3) ![]() , 4)
, 4) ![]() , 5)
, 5) 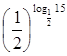 , 6)
, 6) 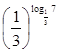 ; 7)
; 7) 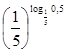 ,
,
8) 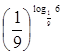 , 9)
, 9) ![]() , 10)
, 10) ![]() , 11)
, 11) ![]() , 12)
, 12) ![]() , 13)
, 13) ![]() ,
,
14) ![]() ,15)
,15) ![]() , 16)
, 16) ![]() , 17)
, 17) ![]() , 18)
, 18) ![]() , 19)
, 19) ![]() , 20)
, 20) ![]() .
.
3. Вычислите: а)![]() ,б)
,б) 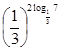 ,
в)
,
в) ![]() ,
,
г)![]() , д)
, д)![]() .
.
4. Упростите выражение :
а) ![]() ;б)
;б) ![]() ,в)
,в)![]() ;
;
5.Вычислить логарифмы: log381,ln e, lg1000, log7343,ln7,29, lg0,001.
6.Вычислить логарифмы: log432 + log42, log552, log2(8 × 128), log654 + log64, log3108 – log34.
7.Вычислить логарифмы: ![]()
8.![]()
9. Вычислите: 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ;
4)
;
4) ![]() ; 5)
; 5) ![]() ;
;
6)
![]() , 7)
, 7) 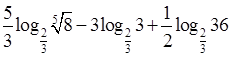 ,
8)
,
8) ![]() .
.
10. Выразите данный
логарифм через натуральный и вычислите на микрокалькуляторе с точностью до 0,01
: 1) ![]() ; 2)
; 2) ![]() .
.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.