
Практическое занятие № 15. Электромагнитные колебания и волны.
Цель: закрепить знания по теме «Электромагнитные колебания и волны», сформировать умения и навыки нахождения физической величины, её выражение из формулы при решении экспериментальных и расчетных задач.
Теоретические сведения.
Аналогия между электрическими и механическими величинами.
|
Электрические величины |
Механические величины |
||
|
Заряд конденсатора |
q (t) |
Координата |
x (t) |
|
Ток в цепи |
|
Скорость |
|
|
Индуктивность |
L |
Масса |
m |
|
Величина, обратная электроемкости |
|
Жесткость |
k |
|
Напряжение на конденсаторе |
|
Упругая сила |
kx |
|
Энергия электрического поля конденсатора |
|
Потенциальная энергия пружины |
|
|
Магнитная энергия катушки |
|
Кинетическая энергия |
|
|
Магнитный поток |
LI |
Импульс |
mυ |
В отсутствие затухания свободные колебания в электрическом контуре являются гармоническими, то есть происходят по закону:
q(t) = q0 cos(ωt + φ0).
Мгновенное значение ЭДС:
![]()
Мгновенное значение напряжения:
![]()
Параметры L и C колебательного контура определяют собственную частоту свободных колебаний:
![]()
Если в колебательном контуре нет потерь энергии, то полная электромагнитная энергия системы остается неизменной:
![]()
Индуктивное сопротивление:
![]()
Емкостное сопротивление:
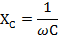
Действующие значения силы тока и напряжения:
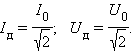
Средняя мощность переменного тока на участке цепи, содержащем резистор, равна:
![]()
Сопротивление цепи переменного тока:
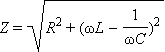
Закон Ома для цепи переменного тока:
ZI0 = ![]() 0.
0.
При резонансе полное сопротивление цепи принимает максимальное значение, равное активному сопротивлению резистора:
Z = Zmax = R
Коэффициент трансформации:
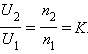
Коэффициент K = n2 / n1 есть коэффициент трансформации. При K > 1 трансформатор называется повышающим, при K < 1 – понижающим.
Электромагнитные волны распространяются в веществе с конечной скоростью:
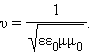
Здесь ε и μ – диэлектрическая и магнитная проницаемости вещества, ε0 и μ0 – электрическая и магнитная постоянные: ε0 = 8,85419·10–12 Ф/м,μ0 = 1,25664·10–6 Гн/м.
Длина волны λ в синусоидальной волне связана со скоростью υ распространения волны соотношением λ = υT = υ / f, где f – частота колебаний электромагнитного поля, T = 1 / f.
Скорость электромагнитных волн в вакууме (ε = μ = 1):
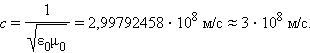
Период свободных колебаний:
![]()
Контрольные вопросы.
1. Что называется колебаниями контура?
2. Нарисуйте схему колебательного контура и объясните все стадии процесса превращения энергии при свободных электрических колебаниях в течение периода колебаний.
3. Запишите формулу Томсона.
4. Что называется действующим значение переменного тока?
5. Какие виды сопротивлений различаются в цепи переменного тока?
6. Опишите процессы, происходящие в контуре при свободных электромагнитных колебаниях.
7. Сформулируйте закон Ома для цепи переменного тока.
8. Что называют трансформатором? Опишите принцип его действия?
9. Что называют электромагнитной волной?
10. Что является источником электромагнитных волн?
11. Перечислите основные свойства электромагнитных волн?
12. Чем отличаются электромагнитные волны от механических?
Задание 1. Выполните эксперимент «Наблюдение интерференционной картины от двух отверстий».
Цель: убедиться, что сложение волн от двух когерентных источников приводит к появлению устойчивой интерференционной картины.
Оборудование: лазерный брелок, фольга (черная бумага), белый экран (бумага), два держателя.
Ход работы
В эксперименте негласно предполагается, что стенка сосуда очень тонкая, т. е. оптическая длина пути в ней мала по сравнению с оптической длиной пути в жидкости: 2nст d << nxL.
1. Укрепите в держателе лазерный брелок горизонтально (рис.40). Кнопка должна быть удобно расположена для нажатия одним пальцем.
|
|
2. Проделайте обыкновенной иглой в фольге от конфет два маленьких (около 0,2 мм в диаметре) отверстия на максимально близком (около 0,5 мм) расстоянии, но не превышающем ширину луча лазера. Можно заменить фольгу черной бумагой, чтобы отраженный от фольги свет не слепил глаза.
3. Укрепите фольгу с отверстиями в держателе так, чтобы оба отверстия были одинаково освещены. Это лучше контролировать с обратной стороны фольги. Если отверстия оказались чуть шире луча, то можно между лазером и фольгой поставить рассеивающую линзу, чтобы уширить луч.
4. Медленно отодвигая одной рукой экран, второй периодически нажимайте кнопку лазерного брелока и наблюдайте, как две светящиеся точки на экране сольются в одну и возникнет интерференционная картина из чередующихся максимумов и минимумов освещенности (темные и светлые полосы). Зафиксируйте экран в месте, где картина наблюдается наиболее четко (при удалении увеличивается расстояние между полосами, но падает яркость).
5. Закройте одно отверстие в фольге бумагой или иглой и пронаблюдайте картину на экране. Зарисуйте эту картину при одном и двух открытых отверстиях.
6. Если у вас есть помощник, а батарейки в брелоке еще не сели, попросите помощника подержать кнопку лазера, а сами измерьте расстояние между двумя максимумами х (х = 0,005/Ν м, где Ν - это число полос на 5 мм). Это дает возможность сравнить расчетную величину х = λL/d (рис. 41) с измеренной (λ - длина волны излучения лазерного брелока, L- расстояние от фольги до экрана, d - расстояние между центрами отверстий).
![]()
7. Сделайте вывод.
Задание 2. Решение задач.
1. Дифракционная решётка содержит 120 штрихов на 1 мм. Найти длину волны монохроматического света, падающего на решётку, если угол между двумя спектрами первого прядка равен 80 .
2. Определить угол отклонения лучей зелёного света (длина волны 0,55 мкм) в спектре первого порядка, полученном с помощью дифракционной решётки, период который равен 0,02 мм.
3. Сколько времени идёт свет от Солнца до Земли?
4. Вода освещена красным светом, для которого длина волны в воздухе 0,7 мкм. Какой будет длина волны в воде?
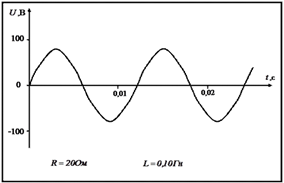
Задание 3. Работа с карточками «График напряжения переменного тока».
1. Какова циклическая частота тока?
2. Определите амплитудное значение напряжения.
3. Вычислите действующее значение напряжения.
4. Вычислите амплитудное и действующее значение тока при включении в цепь только активного сопротивления R, указанного в карточке. Перечертите данный график изменения напряжения со временем и на том же чертеже изобразите графическую зависимость силы тока от времени, выбрав подходящий масштаб.
5. Какова будет средняя мощность тока в этом случае?
6. Вычислите реактивное и полное сопротивление, если в цепь будут включены последовательно активное сопротивление R и катушка с индуктивностью L.
7. Вычислите амплитудное значение тока в этой цепи.
8. Какой емкости конденсатор следует включить последовательно в данную цепь, чтобы получить резонансное увеличение тока?
9. Какое амплитудное напряжение возникнет в этой цепи на индуктивном и емкостном сопротивлениях?
Вариант 1. Вариант 2.
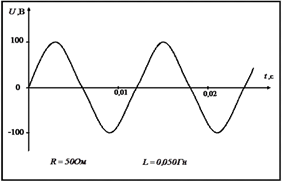
Вариант 3. Вариант 4.
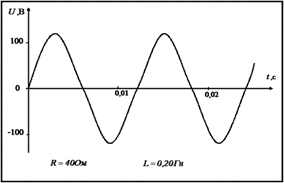
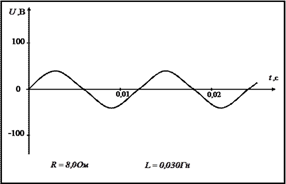
Вариант 5. Вариант 6.
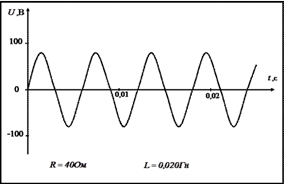
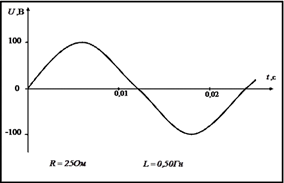
Вариант 7. Вариант 8.
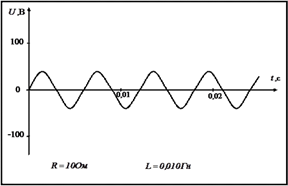
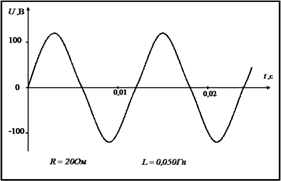
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.