Практическое занятие по теме "Вычисление площадей боковой и полной поверхностей многогранников и тел вращения"

Практическое занятие

Тема: «Вычисление боковой и полной поверхности тел»

Цели: формировать умения и навыки решения задач на вычисление площадей боковой и полной поверхностей многогранников и тел вращения.

Краткая теоретическая справка.

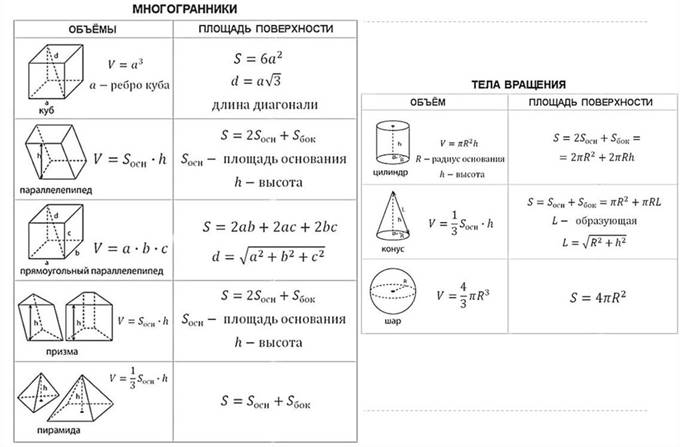
Формулы для вычисления боковой и полной поверхностей

многогранников и тел вращения

Примеры решения задач.

Задача 1. Площадь основания первого конуса в 4 раза меньше, чем площадь основания второго конуса, а образующая первого конуса в 3 раза больше, чем образующая второго. Чему равна площадь боковой поверхности второго конуса, если площадь боковой поверхности первого равна 12?

Решение.

 Подставим эти две формулы в первое выражение, получим:  Сокращаем на π;

Так как , то Подставим выделенные значения:

Задача 2. Осевым сечением цилиндра является квадрат, площадь которого равна 16. Найдите площадь полной поверхности цилиндра.

Решение.

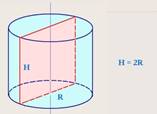
 по условию сечением является квадрат, значит 2R=h, то есть  

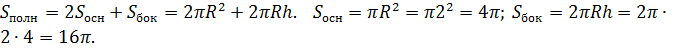
Задача 3. Основание пирамиды - квадрат  со стороной 30 см. Боковые ребра пирамиды равны 25. Найдите площадь боковой поверхности пирамиды.

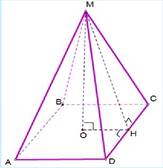
Решение.

Из треугольника MHC (по теореме Пифагора находим апофему

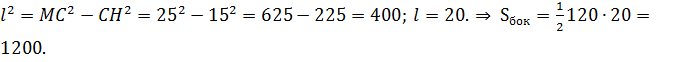
Задача 4. Во сколько раз уменьшится площадь поверхности шара, если его радиус уменьшить в 2 раза?

Решение. 

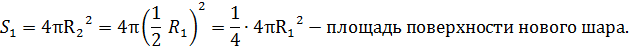
Таким образом, площадь поверхности шара уменьшится в 4 раза.

Задача 5. Диагональ прямоугольного параллелепипеда равна , а стороны основания 3 и 4. Найдите площадь полной поверхности параллелепипеда.

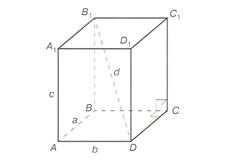Решение:

Подставим в эту формулу данные значения

Решите самостоятельно следующие задачи:

( в задачах1-9 даются комментарии по их выполнению)

1.     Сумма длин всех ребер куба равна 36. Найдите площадь его поверхности.

(подсказка: у куба 12 равных ребе, значит можно найти длину ребра. Площадь полной поверхности состоит из 6 одинаковых квадратов, площадь которого вычисляется по формуле )

2.     Площадь поверхности шара равна 36. Найдите площадь большого круга шара.( Самый большой круг получается в сечении, проходящем через центр шара, вспомните формулу площади круга)

3.     Найдите площадь поверхности прямоугольного параллелепипеда, если его ребра равны 2,3,5.(непосредственная подстановка в формулу данных значений).

4.     Найдите площадь поверхности правильной четырехугольной пирамиды, сторона основания которой равна 6, а апофема равна 4.(сначала вычислите периметр основания, а затем прямая подстановка в формулу).

5.     Площадь боковой поверхности цилиндра равна 36, высота равна 3. Найдите длину окружности основания цилиндра.(из площади боковой поверхности выразить длину окружности).

6.     Площадь основания цилиндра равна 25π, а его высота равна 6. Найдите площадь полной поверхности цилиндра.(из площади основания находим радиус, затем вычисляем площадь боковой поверхности и полной поверхности).

7.     Площадь основания конуса равна 25π. Высота равна 2. Найдите площадь осевого сечения конуса.(осевым сечением конуса является равнобедренный треугольник с основанием, равным 2R и высотой, равной высоте конуса, применить формулу площадь треугольника).

8.     Найдите площадь боковой поверхности правильной треугольной призмы, сторона основания которой равна 3, а высота 2.(непосредственная подстановка).

9.     Диаметр основания конуса равен 14, а образующая -25. Найдите площадь полной поверхности конуса.(сначала найти радиус, непосредственная подстановка).

10. Во сколько раз увеличится площадь боковой поверхности конуса, если радиус его основания увеличится в 4 раза, а образующая уменьшится в 2 раза.

11. Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшится в 3,5 раза, а образующая останется прежней.

12. Во сколько раз уменьшится площадь поверхности куба, если все его ребра уменьшить в 1,5 раза?

13. Параллельно основанию конуса проведено сечение, делящее высоту в отношении 1:3, считая от вершины. Найдите площадь полной поверхности конуса, если площадь полной поверхности усеченного конуса равна 5.

14. Найдите площадь боковой поверхности прямой треугольной призмы, в основании которой лежит прямоугольный треугольник с катетом 5 и гипотенузой 13, если высота призмы равна 2.

15.