Практическое занятие по теме "Вычисление вероятности с помощь. формул комбинаторики"

Тема занятия:  Вычисление вероятности с помощью формул комбинаторики

ЗАДАНИЕ №1. Разберите УСТНО примеры решения задач ниже.

Пример 1. В урне находится 15 белых, 5 красных и 10 чёрных шаров. Наугад извлекается 3 шара, найти вероятность того, что они будут:

а) все белыми, б) все одного цвета,  в) ровно два черных.

Решение: общее количества исходов: всего в урне: 15 + 5 + 10 = 30 шаров, извлекаем три шара. Нам не важно в какой последовательности появятся эти шары. Найдем, сколько всего существует способов извлечь из урны 3 шара: сочетания 3 из 30

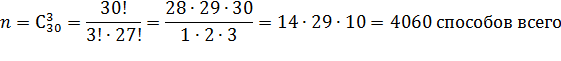
Таким образом, общее число исходов: n=4060

а) Рассмотрим событие: A – «из урны будут извлечены 3 белых шара». Данному событию благоприятствуют m элементарных исходов – в урне всего 15 белых шаров, извлечь все три белых можно (сочетания 3 из 15) 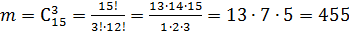 способами.

поэтому по классическому определению:
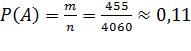 – вероятность того, что из урны будут извлечены 3 белых шара.

б) Событие B –«из урны будут извлечены три шара одного цвета» - означает, что все три шара будут ЛИБО белые, ЛИБО красные, ЛИБО черные. Сначала подсчитаем, сколькими способами из урны можно по отдельности извлечь три красных и три черных шара, так как три белых шара могут быть извлечены 455 способами (см. пункт а)
3 красных шара- (сочетания 3 из 5) 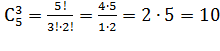 сп.

3 черных шара- (сочетания 3 из 10) 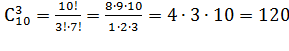 сп.

Так как в этом условии работает логическая связка ИЛИ, по правилу сложения получаем, что три белых, или три красных, или три черных шара можно извлечь 455+10+120 =585 способами, это и будет число m- благоприятных исходов.

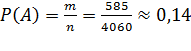 – вероятность того, что из урны будут извлечены 3 шара одного цвета.

в) Событие C –«из урны будут извлечены l два черных шара» - означает, что два  шара будут черные, а третий ЛИБО красный, ЛИБО белый. Таким образом нас устраивает комбинации: 2 черных И 1 красный ИЛИ 2 черных И 1 белый. Сначала подсчитаем, сколькими способами из урны можно извлечь два черных шара:

2 черных шара- (сочетания 2 из 10) 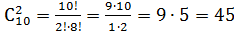 сп.

1 белый шар можно извлечь  

1 красный -

2 черных И 1 белый –

2 черных И 1 красный –

2 черных И 1 белый ИЛИ 2 черных И 1 красный-  675+225=900 сп.

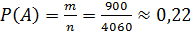 – вероятность того, что из урны будут извлечены ровно 2 черных шара.

Пример 2 .Студент знает ответы на 25 экзаменационных вопросов из 60-ти. Какова вероятность сдать экзамен, если для этого необходимо ответить не менее чем на 2 из 3-х вопросов?

Решение: итак, расклад таков: всего 60 вопросов, среди которых 25 «хороших» и, соответственно, 60 – 25 = 35 «плохих». Ситуация шаткая и не в пользу студента. Давайте узнаем, насколько хороши его шансы:

 способами можно выбрать 3 вопроса из 60-ти (общее количество исходов).

Для того чтобы сдать экзамен, нужно ответить на 2 или 3 вопроса. Считаем благоприятствующие комбинации:

 способами можно выбрать 2 «хороших» вопроса и один «плохой»;

 способами можно выбрать 3 «хороших» вопроса.

По правилу сложения комбинаций:
 способами можно выбрать благоприятствующую для сдачи экзамена комбинацию 3-х вопросов (без разницы с двумя или тремя «хорошими» вопросами).

По классическому определению:
 – вероятность того, что студент сдаст экзамен.

Ответ: 

Пример 3. Найти вероятность того, что при броске двух игральных костей произведение очков:

а) будет равно семи;
б) окажется не менее 20-ти;
в) будет чётным.

 Решение: найдём общее количество исходов:
 способами могут выпасть цифры на 2-х кубиках.

а) Рассмотрим событие:  – при броске двух игральных костей произведение очков будет равно семи. Для данного события не существует благоприятствующих исходов, по классическому определению вероятности:
, т.е. это событие является невозможным.

б) Рассмотрим событие:  – при броске двух игральных костей произведение очков окажется не менее 20-ти. Данному событию благоприятствуют следующие исходы:

Итого: 8 .По классическому определению:
 – искомая вероятность.

в) Рассмотрим противоположные события:
 – произведение очков будет чётным;
 – произведение очков будет нечётным.
Перечислим все исходы, благоприятствующие событию :

Итого: 9 благоприятствующих исходов.
По классическому определению вероятности: 
Противоположные события образуют полную группу, поэтому:
 – искомая вероятность.

Ответ: 

Пример 4. Ребенок имеет на руках 5 кубиков с буквами: А, К, К, Л, У. Какова вероятность того, что ребенок соберет из кубиков слово "кукла"?

Решение: Используем классическое определение вероятности: P=m/n, где n - число всех возможных элементарных исходов, m - число элементарных исходов, благоприятствующих осуществлению события. 

Число различных перестановок с повторениями из букв А, К, К, Л, У равно

 , из них только одна соответствует слову "кукла" (m=1), поэтому по классическому определению вероятности вероятность того, что ребенок соберет из кубиков слово "кукла" равна P=1/60. 

Ответ: 1/60.

         ЗАДАНИЕ №2.  Решите следующие задачи:

1.     Группа туристов, состоящая из 12 юношей и 8 девушек, выбирает дежурных в составе 4 человек. Какова вероятность, что среди них будут 2 девушки?

2.     В урне находится 10 шаров, из них 6 белых и 4 черных шара. Вынули из урны 2 шара. Какова вероятность того, что оба шара - белые?

3.     В ящике 15 деталей, среди которых 10 окрашенных. Сборщик наудачу извлекает три детали. Найти вероятность того, что извлеченные детали окажутся окрашенными. 

4.     Из 5 букв разрезной азбуки составлено слово «книга». Ребенок, не умеющий читать, рассыпал эти буквы, а затем собрал их в произвольном порядке. Найдите вероятность того, что у него получится слово «книга».

5.     В цехе работают шесть мужчин и четыре женщины. По табельным номерам наудачу отобраны семь человек. Найти вероятность того, что среди отобранных лиц окажутся три женщины.

6.     В группе 12 студентов, среди которых 8 отличников. По списку наудачу отобраны 9 студентов. Найти вероятность того, что среди отобранных студентов пять отличников.

7.     В ящике находятся 15 красных, 9 голубых и 6 зеленых шаров. Наудачу вынимают 6 шаров. Какова вероятность того, что вынуты 1 зеленый, 2 голубых и 3 красных шара.

8.     В ящике находится 15 качественных и 5 бракованных деталей. Наудачу извлекаются 2 детали. Найти вероятность того, что:

а) обе детали будут качественными;
б) одна деталь будет качественной, а одна – бракованной; 
в) обе детали бракованны.

Скачано с www.znanio.ru