Практико-ориентированные подход к изучению математики . "Функция и литературные образы"

 

Выступление на МО естественно-научного цикла.

Тема: «Практико-ориентированные задачи и обучение математике. Cвойства  функции и литературные образы»

(Тучак А.З.)

 

         Функция – одно их центральных понятий математики. Оно позволяет дать описание закономерностей, зависимостей величин друг от друга. С большой долей вероятности можно утверждать, что с помощью функций можно перевести на математический язык все процессы, происходящие вокруг нас, произвести исследование на кончике пера природных и социальных явлений, спрогнозировать дальнейшее развитие исследуемых объектов.

         Школьная математика – это не наука, а предмет, основная цель которого – изучение реальных ситуаций с помощью математических моделей, математика изучает реальные ситуации, а первичная математическая модель – функция, поэтому функции, их свойства и графики, как в явной, так и в неявной форме составляют стержень школьного курса математики. Освоение индивидуально заданной функции происходит в сопоставлении черт, специфических для неё, с общим представлением о функции.

           Вместе с тем, являясь одним из ярких примеров абстракции, понятие функции продолжает оставаться наиболее трудно понимаемым учениками средних и старших классов. Для получения подтверждения или опровержения этой мысли было решено провести опрос среди учеников 9-11 классов Гимназии. Мы предложили старшеклассникам выбрать из списка математических понятий, изучаемых в школе, три наиболее трудные для понимания. Затем из трех выбрать только одну с тем же критерием отбора. Анализ ответов старшеклассников показал следующие результаты:

«Функция и ее свойства» -48%»

«Уравнения и неравенства»-21%

«Дробные выражения»-12%

«Последовательности»-8%

«Вероятность»-6%

«Числовые множества»-5%

           Результаты опроса и анализ затруднений при сдаче ОГЭ и ЕГЭ подтвердили наше предположение. Школьная тема «Функция и ее свойства» признана старшеклассниками наиболее трудной для понимания. Это послужило причиной написания данного проекта с целью поиска способов устранения этих трудностей. Бытует мнение, что человеческий мозг обладает функциональной асимметрией: левое полушарие настроено на процедуру рационального, поэтапного аналитического мышления, правое более приспособлено для восприятия целостных образов, одномоментной обработки информации. Человек воспринимает, познаёт и воссоздаёт мир двумя противоположными способами - рассудочным и образным, рациональным и эмоциональным, «мыслью и сердцем». Неравнозначность левого и правого полушарий приводит к условному делению большинства людей на «физиков» и «лириков». Таким образом, сама природа, давая человеку призвание, заботится о том, чтобы развитие культуры было обеспечено приходом как ученых, так и художников. Науку и искусство можно назвать двумя крыльями культуры, они - дополняющие друг друга противоположности, две грани одного и того же процесса - творчества. Школьник, которому приходится видеть математику только в учебнике, неожиданно встречаясь с литературными образами как иллюстрацией математических понятий, подключают к процессу познания оба полушария своего мыслительного аппарата. И, скорее всего, этот факт станет причиной успешного усвоения школьниками традиционно трудных математических тем.

       Приведем цитаты великих людей, которые подтверждают, что мы в своих изысканиях двигаемся в правильном направлении:

а)«…О сколько нам открытий чудных

Готовит просвещенья дух,

И опыт, сын ошибок трудных,

И гений, парадоксов друг…»- так сказал А.С.Пушкин. 

Попытаемся сделать эти открытия, привлекая на помощь литературу.

б)«…Иная шутка, словцо бедовое
Мудрей, чем книжица стопудовая.

Ведь не таблицею умножения

Подчас является к нам прозрение?»

(Из стихотворения Владимира Михановского "Мечта")

  в)    «… Гуманитарные науки. только тогда будут удовлетворять человеческую мысль, когда в движении своём они встретятся с точными науками и пойдут с ними рядом…»

А. П. Чехов

      Сочетать несочетаемое - привычная работа нашего воображения, когда мы ищем объяснение непонятному.   Интеграция - естественный способ познания себя и окружающего мира, который выражается в сочетании эстетического, познавательного, историко-генетического, общественно-функционального аспектов.

Гипотеза: Если при изучении трудной математической темы «Функция и ее свойства» использовать литературные образы как иллюстрации и аналогии, то это будет способствовать лучшему пониманию темы, качественному изучению.

Актуальность выбранной темы - увидеть за литературным сюжетом – функцию, ее свойства и доказать, что художественная литература способствует лучшему пониманию математики, превращает абстрактные объекты в понятные и естественные.

Цель исследования - поиск в литературе художественных образов, аналогичных по строению или смыслу понятию «функция», отражающих ее свойства. Объяснение причин выбора.  Доказательство способствования литературы пониманию математических понятий.

Объект исследования: произведения русской классической и современной художественной литературы. Факты из жизни отдельных математиков и поэтов.

Задачи исследования:

1) изучение научно-популярной, занимательной русской литературы;

2) подбор художественной литературы для исследования;

3) решение задач и оценка полученных результатов;

4) создание буклета и его апробация.

Методы исследования: анализ научно-популярной и занимательной литературы, анализ и синтез точной науки с художественными аналогами, сравнение результатов с реальной действительностью.

 

 

 

 

 

 

 

 

 

1.Исторические сведения.

Идея функциональной зависимости восходит к древности. Ее содержание обнаруживается уже в первых математически выраженных соотношениях между величинами, в первых правилах действий над числами. В первых формулах для нахождения площади и объема тех или иных фигур. Так, вавилонские ученые (4 – 5 тыс. лет назад) пусть и несознательно, установили, что площадь круга является функцией от его радиуса посредством нахождения грубо приближенной формулы: S=3r2. Примерами табличного задания функции могут служить астрономические таблицы вавилонян, древних греков и индийцев, а примерами словесного задания функции — теорема о постоянстве отношения площадей круга и квадрата на его диаметре или античные определения конических сечений, причем сами эти кривые выступали в качестве геометрических образов соответствующей зависимости.

Путь к появлению понятия функции заложили в 17 веке французские ученые Франсуа Виет и Рене Декарт; они разработали единую буквенную математическую символику, которая вскоре получила всеобщее признание. Введено было единое обозначение: неизвестных — последними буквами латинского алфавита: x, y, z, известных — начальными буквами того же алфавита: a, b, c,... и т. д. Под каждой буквой стало возможным понимать не только конкретные данные, но и многие другие; в математику пришла идея изменения. Тем самым появилась возможность записывать общие формулы. Кроме того, у Декарта и Ферма (1601 – 1665) в геометрических работах появляется отчетливое представление переменной величины и прямоугольной системы координат.     В 1671 году Ньютон под функцией стал понимать переменную величину, которая изменяется с течением времени (он называл ее "флюентой").

В "Геометрии" Декарта и работах Ферма, Ньютона и Лейбница понятие функции носило, по существу, интуитивный характер и было связано либо с геометрическими, либо с механическими представлениями: ординаты точек кривых — Само слово "функция" (от латинского functio — совершение, выполнение) впервые было употреблено немецким математиком Лейбницем в 1673 г. в письме к Гюйгенсу (под функцией он понимал отрезок, длина которого меняется по какому-нибудь определенному закону), в печати он его ввел с 1694 года. Начиная с 1698 года Лейбниц ввел также термины "переменная" и "константа".

В 18 веке появляется новый взгляд на функцию как на формулу, связывающую одну переменную с другой. Это так называемая аналитическая точка зрения на понятие функции. Подход к такому определению впервые сделал швейцарский математик Иоганн Бернулли (1667 – 1748), который в 1718 году определил функцию следующим образом: "функцией переменной величины называют количество, образованное каким угодно способом из этой переменной величины и постоянных".

Наряду с этим Эйлер предлагает использовать буквы F, Y и другие. Даламбер сделал шаг вперед на пути к современным обозначениям, отбрасывая двоеточие Эйлера; он пишет, например, jt, j (t+s).

Окончательную формулировку определения функции с аналитической точки зрения сделал в 1748 году ученик Бернулли Эйлер (во "Введении в анализ бесконечного"): "Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого количества и чисел или постоянных количеств". Так понимали функцию на протяжении почти всего 18 века Даламбер (1717 – 1783), Лагранж (1736 – 1813), Фурье (1768 – 1830) и другие видные математики.

Большой вклад в разрешение спора Эйлера, Даламбера, Бернулли и других ученых 18 века по поводу того, что стоит понимать под функцией, внес французский математик Жан Батист Жозеф Фурье (1768 – 1830), занимавшийся в основном математической физикой. В представляемых им в Парижскую АН в 1807 – 1811 гг. "Мемуарах по теории распространения тепла в твердом теле", Фурье привел и первые примеры функций, которые заданы на различных участках различными аналитическими выражениями. Из трудов Фурье следовало, что любая кривая, независимо от того, из скольких и каких разнородных частей она состоит, может быть представлена в виде единого аналитического выражения и что имеются также прерывные кривые, изображаемые аналитическим выражением. В своем "Курсе алгебраического анализа", опубликованном в 1721 г., французский математик О. Коши обосновал выводы Фурье. Таким образом, на известном этапе развития физики и математики стало ясно, что приходится пользоваться и такими функциями, для определения которых очень сложно или даже невозможно ограничиться одним лишь аналитическим аппаратом. Во второй половине 19 века после создания теории множеств в понятие функции, помимо идеи соответствия была включена и идея множества. Таким образом, в полном своем объеме общее определение понятия функции формулируется следующим образом: если каждому элементу x множества А поставлен в соответствие некоторый определенный элемент y из множества В, то говорят, что на множестве А задана функция y=f(x), или что множество А отображено на множество В. В первом случае элементы x множества А называют значениями аргумента, а элементы их множества В - значениями функции; во втором случае x - прообразы, y – образы – определение Дирихле. Синонимами термина “функция” в различных отделах математики являются: соответствие, отображение, оператор, функционал и др. Определение функции Дирихле стало классическим. 

2.Что такое функция.

Прежде чем дать точное определение функции, поговорим немного об этом понятии. Описательно говоря, функция – это когда каждому значению некоторой величины, которую математики называют аргументом и обозначают обычной буквой x, отвечает значение другой величины y. Так, например, величина смещения земной поверхности при землетрясении в каждый момент времени имеет определенное значение – величина смещения есть функция времени. Сила тока в полупроводниковом элементе есть функция напряжения, так как каждому значению напряжения соответствует определенное значение силы тока. Теперь мы можем более точно сказать, что такое функция.

Функция – это зависимость y = f ( x ), где каждому элементу x соответствует единственное значение функции y, где y – значение функции (зависимая переменная), x – значение аргумента (независимая переменная).Еще одно существенное замечание. Когда говорят, что величина y есть функция величины x, то, прежде всего, указывают, какие значения может принимать x . Эти «разрешенные» значения аргумента x называют допустимыми значениями, а множество всех допустимых значений величины называется областью определения функции y.  Например, если мы говорим, что объем шара есть функция его радиуса, то областью определения функции будут все числа, больше нуля, поскольку величина радиуса шара может быть только положительным числом.

При изучении определения функции привлекаем на помощь литературный образ, точнее одна из любопытных гипотез закономерности или соответствия формы написания арабских цифр и количества углов в их начертании. Объяснить принцип начертания цифр попытался директор Maрокканского государственного музея истории Абделькри Боужибар. Он лишь состоит в следующем, арабским цифрам в их первоначальном варианте было придано значение в строгом соответствии с числом углов, которые образуют иероглифы цифр.

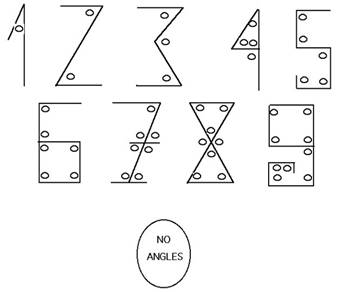Так, иероглиф, изображающий цифру 1, образует один угол, иероглиф 2 - два угла, 3 - три угла и т. д. Это, несомненно, остроумная и удачная догадка. По безупречности сродни стихам. Вместе с тем это несомненно пример функции с математической точки зрения. Аргумент-знак цифры, функция- количество углов в начертании цифры. Область определения данной функции –множество цифр, область значений –количества углов от 0 до 9.

  Такой пример соответствия или функции в ее строгом смысле значительно приближает учеников к пониманию определения и сопутствующим обозначениям, элементам.  Яркой иллюстрацией определения функции или попыткой создать ее художественный образ являются рисунки детей, выполненные на интуитивном уровне (рис.1 и рис.2, приложение).

    Еще один литературный образ для понятия функция, еще одно однозначное соответствие.

«Пляшущие человечки»  Конан Дойля.Каждой фигурке единственным образом ставится в соответствие буква алфавита. Перед нами еще один любопытный пример функциональной зависимости, который может сослужить добрую службу в деле понимания абстрактной математической формулировки. (Приложение 1)

 

3.Свойства функции.

3.1.Монотонность функции.

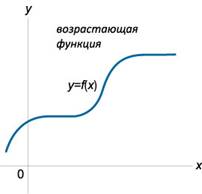 Функция y=f(x) называется возрастающей на интервале (a;b), если для любых x₁ и x₂ из этого интервала таких, что x₁<x₂, справедливо f(x₁)<f(x₂). Функция y = f(x) называется убывающей на интервале (a;b), если для любых  x₁ и x₂ из этого интервала таких, что x₁<x₂, справедливо f(x₁)>f(x₂)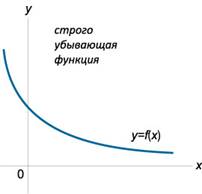        

У Пушкина на эту тему есть строки (Неточная цитата из романа в стихах «Евгений Онегин» (1823—1831) А. С. Пушкина (1799—1837) (гл. 4, строфа 7)::

 

Чем меньше женщину мы любим,

Тем легче нравимся мы ей

И тем ее вернее губим

Средь обольстительных сетей.

Ему вторит П.Вяземский:

Чтоб более меня читали,

Я стану менее писать…

Снова убывание, снова вопреки логике, снова парадокс.

Описанная ситуация в романе есть ни что иное как пример убывающей функции.

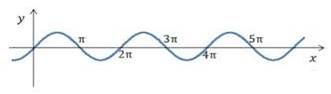
3.2.Периодичность функции.

Литературный образ отражающий это свойство некоторых функций- это стихотворение Самуила Маршака «Дом, который построил Джек».(Приложение 2)

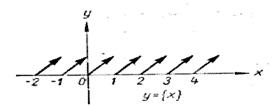Способ построения стихотворения напоминает движение бесконечной периодической волнообразной синусоиды или структуру повторяющегося графика функции «дробная часть числа х».

 

 

 

3.3.Суперпозиция функций.

 f (g(n(x)))- «матрешкообразная» функция, у которой аргумент и сам является функцией. Примеры суперпозиции функции:у= (sin x -5x)³ ; f(x)=log_x-3(4x+e^x)

В литературе суперпозиция функций выглядит примерно так:	Если перевести стихотворение на язык символов, то это выглядит следующим образом: g(a(k(l(p(x)))).
Не было гвоздя – Подкова Пропала. Не было подковы - Лошадь Захромала. Лошадь захромала - Командир Убит. Конница разбита -- Армия Бежит. Враг вступает в город, Пленных не щадя, Оттого, что в кузнице Не было гвоздя.	g- падение города; a-отступление армии; k-гибель командира; l- травма лошади; p-потеря подковы; х –отсутствие гвоздя.

3.4.Четные функции.  Функция у = f (x) называется чётной, если она не меняется, когда независимая переменная изменяет только знак, то есть, если f (—x) = f (x). Необходимым условием четности функции является симметричность относительно начала координат ее области определения. Необыкновенной иллюстрацией четной функции являются палиндромы- словесные конструкции, которые обладают симметрией подобно симметрии графиков четных функций.

               

 

 

 

 

 

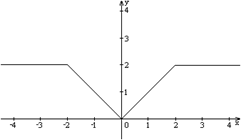
Палиндромы.

1) Аргентина манит негра.

2)Кирилл лирик.

3)А роза упала на лапу Азора. (Автор данного палиндрома Афанасий Фет)

4)В. Брюсов:
  «Жестоко — раздумье. Ночное молчанье
Качает виденья былого,
Мерцанье встречает улыбки сурово.
Страданье —
Глубоко — глубоко!
Страданье сурово улыбки встречает…
Мерцанье былого — виденье качает…
Молчанье, ночное раздумье, — жестоко!»(Приложение 3)

3.5.Нечетные функции.

Примером такой функции служит f(x)=k/x ,обратная пропорциональность или у=х³.Графики этих функций в силу нечетности симметричны относительно начала координат.Их названия гипербола и кубическая парабола.

          

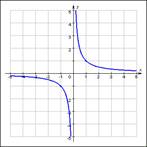
Художественный образ нечетной функции-картины Маурица Эшера «Рисующие руки» и «Лист Мебиуса». (Приложение 4)

3.6.Экстремумы функции и точки экстремумов.
Функция y = f(x) называется возрастающей (убывающей) в некотором интервале, если при x₁< x₂ выполняется неравенство (f(x₁) < f (x₂) (f(x₁) > f(x₂)). Точка x_о называется точкой локального максимума (минимума) функции f(x), если существует окрестность точки x_о, для всех точек которой верно неравенство f(x) ≤f(x_о) (f(x) ≥ f(x_о)). Точки максимума и минимума называются точками экстремума, а значения функции в этих точках - ее экстремумами . Для того, чтобы вдохнуть жизнь в предшествующие формулировки используем исторический нюанс и легенду о максимальном участке земли.

Из античной истории. Задачи на экстремум занимали даже древних мудрецов. Греческие учёные с успехом разгадали тайну площадей и объёмов путём математических вычислений. Это они первыми поняли, что на плоскости из разнообразных фигур, обладающих одним и тем же периметром, наибольшую площадь всегда имеет круг. Аналогичным образом шар наделён максимальным объёмом среди остальных предметов в пространстве с одинаковой величиной поверхности. Решению подобных задач посвятили себя такие известнейшие личности, как Архимед, Евклид, Аристотель, Аполлоний. Найти точки экстремума прекрасно удавалось Герону, который, прибегнув к расчётам, сооружал хитроумные устройства. К ним относились автоматы, перемещающиеся посредством пара, работающие по тому же принципу насосы и турбины.

Существует легенда, сюжет которой построен на решении одной из экстремальных задач. Результатом делового подхода, который продемонстрировала финикийская царевна, обратившаяся за помощью к мудрецам, стало строительство Карфагена. Земельный участок для этого древнего и прославленного города подарил Дидоне (так звали правительницу) вождь одного из африканских племён. Площадь надела не показалась ему вначале очень большой, так как по договору должна была покрываться воловьей шкурой. Но царевна повелела своим воинам разрезать её на тонкие полосы и составить из них ремень. Он получился настолько длинным, что охватил участок, где уместился целый город.

         А теперь перенесёмся из античных времён в более позднюю эпоху. Интересно, что к осознанию основ математического анализа подтолкнула Кеплера в XVII веке встреча с продавцом вина. Торговец был настолько сведущ в своей профессии, что легко мог определить объём находящегося в бочке напитка, просто опуская туда железный жгут. Размышляя над подобным курьёзом, знаменитый учёный сумел решить для себя эту дилемму. Оказывается, искусные бочары тех времён наловчились изготавливать сосуды таким образом, чтобы при определённой высоте и радиусе окружности скрепляющих колец они имели максимальную вместимость.

Это стало для Кеплера поводом для дальнейших размышлений. Бочары пришли к оптимальному решению методом долгого поиска, ошибок и новых попыток, передавая свой опыт из поколения в поколение. Но Кеплер хотел ускорить процесс и научиться делать то же самое в короткий срок путём математических вычислений. Все его наработки, подхваченные коллегами, превратились в известные ныне теоремы Ферма и Ньютона - Лейбница.

 

3.7.Графики функции .

Гипербола .Примеры гиперболы в литературе:

 - «что взмах – то готова копна» Н. А. Некрасов;

- «шириною с Черное море» Н. В. Гоголь о казацких шароварах;

 - «дунул, и поднялся ветер» русские народные сказки;

- «храпит, как трактор» И. Ильф, Е. Петров;

 - «мело, мело по всей земле» Б. Пастернак.

«…Пусть заполнится годами жизни квота,

стоит только вспомнить это диво,

раздирает рот зевота

шире Мексиканского залива…»       

(В.Маяковский , «6 монахинь»)

«Гиперболо́ид инженера Га́рина» — фантастический роман А. Н. Толстого, завершённый к 1927 году. Существует мнение, что более правильным названием устройства Гарина должно было бы быть параболоид, Толстой соглашался с этим и говорил, что об этом знает, однако выбрал слово «гиперболоид» из-за более внушительного звучания. Однако в устройстве Гарина по его описанию использовались два гиперболических зеркала — главное вогнутое и малое выпуклое. Это похоже на систему телескопа Ричи — Кретьена, которая была предложена в 1924 году: она включает в себя два гиперболических зеркала и используется сейчас в большинстве крупных телескопов и в резонаторах мощных лазеров. (Приложение 5)

Математически гипербола- название графика обратной пропорциональности, кривая, относящаяся к числу конических сечений.

Заключение.

Работая над данной темой графики функции раскрылись мне в необычной форме.

Во-первых, мне удалось систематизировать знания, умения и навыки по построению, исследованию функций, изучаемых в школе. Я разобралась в определении функции и научилась определять их свойства, отличать графики функций от графиков уравнений.

Во – вторых, в моей работе видно, что графики функций выходят далеко за пределы курса математики. Во многих профессиях пригодится умение читать графики.

Ещё мне удалось проследить за историей развития понятия функции: на протяжении многих веков учёные постепенно приходили к тому определению функции, которое мы изучаем.

И, наконец, моя работа пригодится мне для сдачи экзамена в форме ЕГЭ в11 классе.

 

 

 

IV. Литература

1.                  Виленкин Н. Я. Функции в природе и технике: Книга для внеклассного чтения 9 – 10 кл. – 2 – е изд., испр. – М.: Просвещение, 1993.

2.                  Глейзер Г.И. История математики в школе.- М., Просвещение, 1981.

3.                  Нагибин Ф.Ф. Математическая шкатулка.- М., Просвещение, 1964.

4.                  Лиман М.М. Школьникам о математике и математиках.- М.: Просвещение, 1981.

5.                  Степанов В.Д. Активизация внеурочной работы по математике в средней школе: Кн. Для учителя: Из опыта работы. – М.: Просвещение, 1991.

6.                  Ульяновская Н. Н. О, функция, как ты Важна // Математика. – 1999. - №45.

7.                  Энциклопедический словарь юного математика. Составитель Савин А.П.- М., Просвещение, 1985.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Приложение 1.

 

Приложение 2.

Вот дом,
Который построил Джек.

А это пшеница,
Которая в тёмном чулане хранится
В доме,
Который построил Джек.

А это весёлая птица-синица,
Которая часто ворует пшеницу,
Которая в тёмном чулане хранится
В доме,
Который построил Джек.

Вот кот,
Который пугает и ловит синицу,
Которая часто ворует пшеницу,
Которая в тёмном чулане хранится
В доме,
Который построил Джек.

Вот пёс без хвоста,
Который за шиворот треплет кота,
Который пугает и ловит синицу,
Которая часто ворует пшеницу,
Которая в тёмном чулане хранится
В доме,
Который построил Джек.

А это корова безрогая,
Лягнувшая старого пса без хвоста,
Который за шиворот треплет кота,
Который пугает и ловит синицу,
Которая часто ворует пшеницу,
Которая в тёмном чулане хранится
В доме,
Который построил Джек.

А это старушка, седая и строгая,
Которая доит корову безрогую,
Лягнувшую старого пса без хвоста,
Который за шиворот треплет кота,
Который пугает и ловит синицу,
Которая часто ворует пшеницу,
Которая в тёмном чулане хранится
В доме,
Который построил Джек.

А это ленивый и толстый пастух,
Который бранится с коровницей строгою,
Которая доит корову безрогую,
Лягнувшую старого пса без хвоста,
Который за шиворот треплет кота,
Который пугает и ловит синицу,
Которая часто ворует пшеницу,
Которая в тёмном чулане хранится
В доме,
Который построил Джек.

Вот два петуха,
Которые будят того пастуха,
Который бранится с коровницей строгою,
Которая доит корову безрогую,
Лягнувшую старого пса без хвоста,
Который за шиворот треплет кота,
Который пугает и ловит синицу,
Которая часто ворует пшеницу,
Которая в тёмном чулане хранится
В доме,
Который построил Джек.

 

Приложение 3

 

 

 

 

 

 

 

            

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Приложение 4

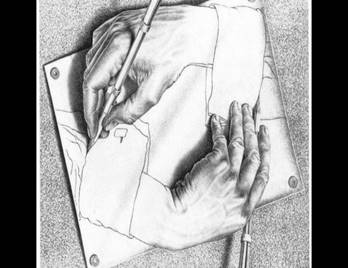Лист бумаги прикреплен к доске кнопками. Правая рука делает на листе набросок манжеты с запонкой. Работа еще не закончена, но справа уже детально прорисована левая рука: она высовывается из рукава так реалистично, словно вырастает из плоской поверхности, и, в свою очередь, делает набросок другой манжеты, из которой, подобно живому, существу выползает правая рука.

 

 

 

 

Лист Мебиуса

М. К. Эшер

 

 

 

 

 

 

 

 

 

Приложение 5

Гиперболоид инженера Гарина.

 

 

 

 

 

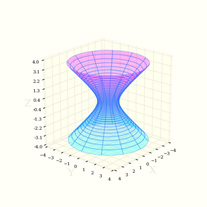
Приложение 6

И еще графики(уравнений), но очень красиво:

 

 

 

 

 

 

 

 

 

 

 

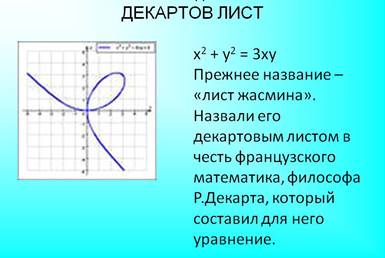
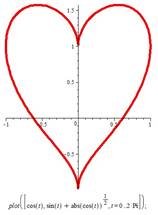
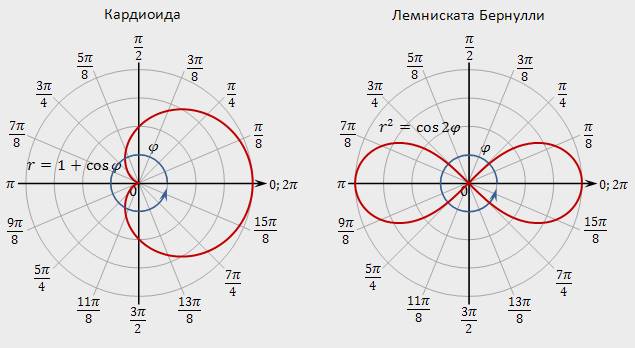
Дети рисуют функцию:

Рис 11.Параболическая орбита со спутником.

Рис 12. Вращающийся сосуд с жидкостью.

 

Функциональные зависимости и юмор.

Чем проще идея, тем сложнее ее излагают –убывающая линейная

Размер доклада о достигнутых результатах обратно пропорционален достигнутым результатам- убывающая пропорциональность, гипербола

Чем хуже стрижка, тем медленнее отрастают волосы-возрастание линейная

Тот, кто живет ближе всех, всегда опаздывает- убывание

Чем проще что-то выглядит, тем больше проблем таит -убывание

Чем длиннее название должности, тем менее важна связанная с ней работа-убывание

Чем короче очередь у кассы, тем медленнее она движется-возрастание

 

 Перевал Парабола                           

   (Западный Саян)                       

 

Скачано с www.znanio.ru