Правильный выпуклый многоугольник

Тип урока: введение нового материала.

Название урока: правильный выпуклый многоугольник.

Цели урока:

•      образовательная:           изучить         определение             и         свойства       правильных многоугольников;

•      развивающая: развивать логическое мышление учащихся посредством использования логических операций: сравнения, обобщения, анализа и синтеза;

•      воспитательная: способствовать       воспитанию трудолюбия,            умения преодолевать трудности для достижении цели.

Задачи урока:

1.      сформулировать определение правильных многоугольников;

2.      познакомить учащихся с формулами «Сумма углов в многоугольнике» и

«Градусная мера угла в правильном многоугольнике»;

3.      показать применение формул при решении задач.

Методы    обучения:    сочетание     репродуктивного,   частично       поискового   и исследовательского.

Формы деятельности: парная, групповая, фронтальная с классом.

Оборудование:          компьютеры,      интерактивно-геометрическая       среда      (ИГС)

«GeoGebra», бумага, ножницы, транспортиры и линейки.

 

 

Заранее учащаяся разбиваются на две группы, группы должны быть одинаковыми (количество человек, уровень знаний). Урок сопровождается презентацией.

Ход урока.

1.  Организационный момент.

2.  Подготовительный этап к введению нового материала.

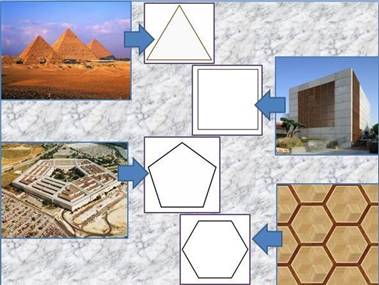
Учитель. Рассмотрите изображения и назовите геометрическое фигуры, которые здесь скрыты (слайд 1).

Учащиеся. 1) Равносторонний треугольник. 2) Квадрат. 3) Пятиугольник.

4) Шестиугольник. (слайд 2).

 

 

Учитель. О каких фигурах пойдёт речь на уроке? (Слайд 3). Чем отличаются представленные многоугольники от других геометрических фигур?

Учащиеся. Правильные геометрические фигуры. Правильные многоугольники.

Учитель. Запишем в тетрадях тему урока "Правильные многоугольники". Сформулируем цель и задачи данного урока. Как вы думаете, что мы будем сегодня изучать?

Учащиеся. Познакомиться с понятием правильного многоугольника, дать определение. Изучим свойства правильных многоугольников.

Учитель. Учителю необходимо корректировать ответы учащихся, при необходимости добавить две последние задачи урока. А также требуется познакомиться с способами (формулами) нахождения суммы углов многоугольника и нахождение градусной меры угла многоугольника. (Слайд 4).

Цель урока: изучить свойства правильных многоугольников.

Задачи урока: 1. сформулировать определение правильных многоугольников;

2.  познакомиться с формулой «Сумма углов в многоугольнике»;

3.  познакомиться с формулой «Градусная мера угла в правильном многоугольнике».

3. Изучение нового материла. Определение.

Учитель. С чего начнём изучение новой темы?

Учащиеся. С определения правильного многоугольника.

Учитель.   Чем     отличаются правильные многоугольники,    от        других многоугольников?

Учащиеся. У этих многоугольников углы и стороны равны. Например, квадрат и прямоугольник.

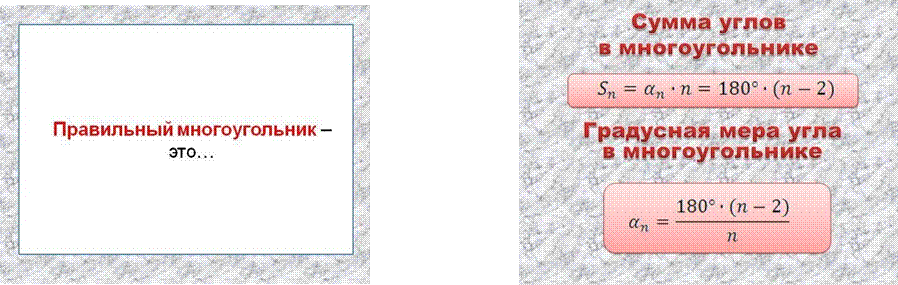
Учитель. Используя данные отличительные признаки сформулируйте определение правильных многоугольников. (слайд 5).

Учащиеся.           Правильный       многоугольник,       это       геометрическая       фигура

(многоугольник) у которой все стороны и углы равны.

Учитель. Мы выдвинули гипотезу, о том, что правильный многоугольник - это многоугольник, у которого все стороны и углы равны. Теперь проверим её.

Учащиеся делятся на две группы: 1 группа работа с ИГС GeoGebra. 2 группа графически-измерительная работа с помощью бумаги, карандаша, ножниц и использует измерительные инструменты (транспортир, линейка). Выполнение работы происходит одновременно.

1 группа. Выполнить построение правильных (выпуклых) многоугольников и измерить их элементы (равные стороны и равные углы) используя инструкции.

Сделать выводы.

Инструкция № 1 по теме "Правильные многоугольники"

 

Цель работы: исследовать свойства правильного многоугольника с помощью интерактивно-геометрической среды GeoGebra.

Всплывающая подсказка. При наведении курсора на инструменте, появляется всплывающая подсказка, которая объясняет, как пользоваться инструментом.

1.         Запустите программу "GeoGebra", ярлык  расположен на рабочем столе.

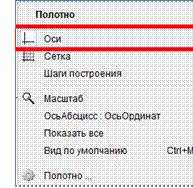
2.         Чтобы убрать координатные оси, наведите курсор на рабочее поле программы → вызовите меню (щелчок левой кнопкой мыши) → выберите в меню

"оси".

 

 

3.         Для удобства работы с программой GeoGebra создадим модель многоугольника, у которого количество сторон "n" будет изменяться. Не забываете, что первая фигура образуется при значении n=3 (треугольник).

Воспользуемся инструментом "ползунок", который позволит изменять значение n.

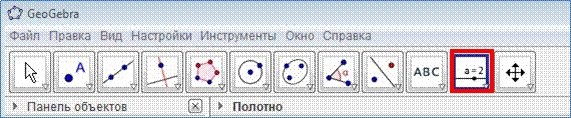
4.         На панели инструментов выберите инструмент "ползунок" и щёлкните в любом месте рабочего поля.

 

 

5.         В появившемся окне последовательно задайте параметры предложенные ниже.

 

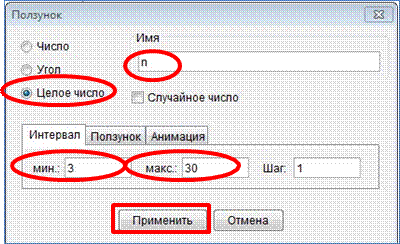
6.         На панели инструментов найдите и выберите инструмент "Правильный многоугольник". Постройте его, воспользовавшись всплывающей подсказкой (см. начало инструкций).

 

 

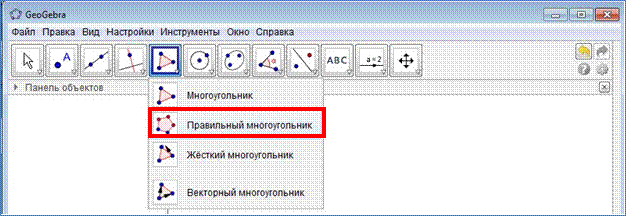
7.         В появившемся окне укажите количество вершин n. Нажмите "ОК".

 

 

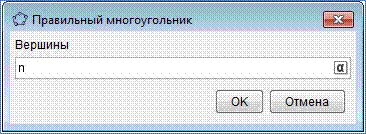
8.         Для изменения сторон правильного многоугольника обязательно выберете инструмент "перемещать"       и двигайте точку на "ползунке"

  .

9.         Для исследования многоугольника вам понадобиться инструменты "угол"   и "расстояние и длина" . Их вы найдёте на панели инструментов.

 

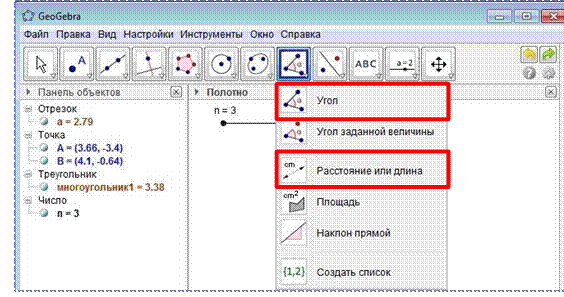
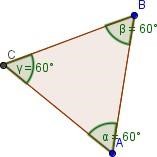
1)                  Выберите инструмент "угол" и укажите область внутри многоугольника. Если вы выполнили всё верно, получите следующий результат:

2)                  Выберите инструмент "расстояние и длина" и укажите все стороны многоугольника, то есть щелкните указателем мыши по сторонам многоугольника.

(Значение длин сторон совпадать не будет).

 

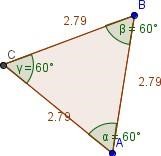
6.         Начните исследование свойств многоугольника. Сделайте вывод и запишите в тетрадь.

7.         Выберите: Файл → Сохранить → Имя файла (место сохранения) → Сохранить.

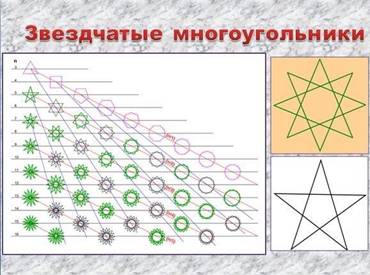
2 группа. С помощью карандаша и линейки построить n-угольные звёзды (звёздчатые многоугольники). Вырезать и исследовать их с помощью линейки и транспортира (слайд 6). Сделать вывод.

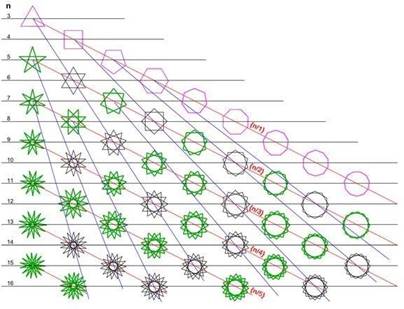
Учащиеся 1 группы. С помощью инструмента "Правильный многоугольник" можно построить многоугольники у которого все стороны и углы равны.

Первая группа подтверждает гипотезу, но вторая группа приводит контрпример. Появляется дискуссия.

Учащиеся 2 группы. У звёзд выполняются свойства правильного многоугольника.

Учитель ещё раз строит несколько правильных многоугольников в ИГС. Учитель. Так как инструмент "правильный многоугольник" не позволяет построить звёздчатый многоугольник, то нужно искать свойство которое позволяет отличить его от правильного многоугольника.

Учащиеся. У звёздчатых многоугольников есть вогнутости, а у правильных многоугольников нет. У правильных многоугольников есть свойство выпуклости. Учитель. Выпуклым многоугольником называют многоугольник, где все его точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Теперь вернёмся к нашей гипотезе и сделаем вывод.

Учащиеся. Гипотеза неверна.

Учитель. Переформулируем определение, внесём коррективы.

Определение.     Правильным            многоугольником, называют      выпуклый многоугольник, у которого все стороны и углы равны. (слайд 5).

Смена мест групп.

4. Изучение нового материала. Формула для вычисления угла правильного многоугольника.

Учитель. Перейдём к следующей задачи урока. Каждой из групп требуется вывести формулу, как найти сумму углов правильного многоугольника. Что для этого вам необходимо знать?

Учащиеся. Количество углов правильного многоугольника и градусную меру одного угла. Заполните выданную таблицу. Где n соответствует количеству сторон и количеству углов.

Записать формулу на доске          . Обратить внимание, что n- количество сторон (латинский алфавит), - градусная мера угла (греческий алфавит).

n	Процесс вычисления
5
7
9
11
...
n

Сумма углов правильного           2 группа. Учащиеся по два человека многоугольника работают            в          ИГС   GeoGebra      с          помощью инструкций.     Каждому       отводится     роль: регистратор и эксперт (эксперт выполняет работу над       исследованиями,    регистратор фиксирует данные).

Разбейте многоугольник на треугольники и запишите процесс нахождения суммы углов.

Инструкция.

Инструкция № 2 по теме "Правильные многоугольники"

 

Цель работы: исследовать углы правильного многоугольника с помощью интерактивно-геометрической среды GeoGebra для вывода формулы "Сумма углов многоугольника".

Всплывающая подсказка. При наведении курсора на инструменте, появляется всплывающая подсказка, которая объясняет как пользоваться инструментом.

1.         Запустите программу "GeoGebra", ярлык  расположен на рабочем столе.

2.         Чтобы убрать координатные оси, наведите курсор мыши на рабочее поле программы → вызовите меню (щелчок левой кнопкой мыши) → выберите в меню

"оси".

 

 

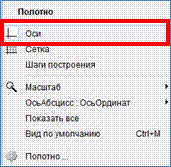
3.         На панели инструментов выберите инструмент "правильный многоугольник".

 

 

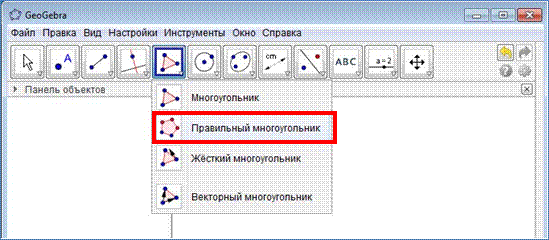
4.         На рабочем поле укажите две точки и нужное вам количество сторон многоугольника.

 

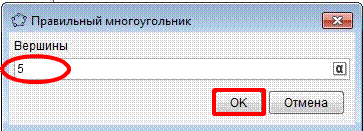
5.         Разобьем многоугольник на треугольники с помощью инструмента

"отрезок по двум точкам".

 

 

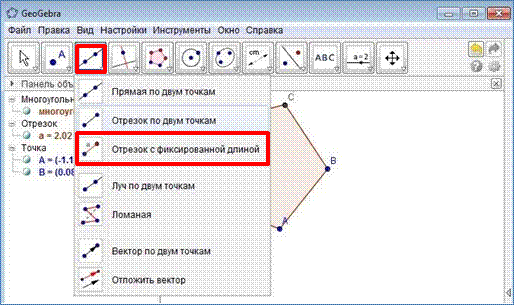
При необходимости воспользуйтесь всплывающей подсказкой (см. начало инструкций).

 

Если вы выполнили всё правильно, то вы получите результат указанный

ниже.

 

 

 

 

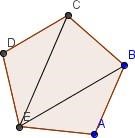
6.         Выберите инструмент "угол" (вершины угла указывайте по часовой стрелке) и примените его к вашему n-угольнику.

 

7.         Заполните выданную таблицу и выведите закономерность. Запишите формулу суммы углов в последней строчке.

Сумма углов правильного многоугольника

n	Процесс вычисления
5
7
9
11
...
n

 

8.         Выберите: Файл → Сохранить → Имя файла (место сохранения) → Сохранить.

 

 

1 группа.   Предлагается           разбить         каждый         правильный многоугольник       на треугольники, соединив одну вершину с остальными, и записать процесс нахождения суммы углов в таблицу.

n	Процесс вычисления
5	180*3
7	180*5
9	180*7
11	180*9
...
n	180*(n-2)

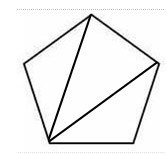Сумма углов правильного многоугольника

Учитель. Сделайте выводы. Можно ли проще найти сумму углов правильного многоугольника.

Учащиеся. Что бы найти сумму углов в правильном многоугольнике, достаточно знать количество сторон.

Фиксация формулы на доске. Проверка.

𝑆_𝑛 = 𝛼_𝑛 · 𝑛 = 180° · (𝑛 − 2)

Учитель. Тогда как из данной формулы выразить градусную меру одного угла правильного многоугольника?

180° · (𝑛 − 2)

𝛼_𝑛 =

𝑛

5.  Первичная проверка понимания. (слайды с 8-11).

Задание 1. Найдите сумму углов правильного n-угольника: а) n=3; б) n=4; в) n=7; г) n=6.

Задание 2. Найдите угол правильного n-угольника: а) n=4; б) n=7; в) n=8.

Задание 3. Сколько сторон имеет правильный многоугольник, если каждый угол равен: а) 108^о; б) 120 ^о; в) 140 ^о.

6.  Подведения итогов урока.

Назовите свойства правильного многоугольника (равны стороны, углы и выпуклость).

Используя свойства сформулируйте определение правильного многоугольника.

Как найти сумму углов? (𝑆_𝑛 = 𝛼_𝑛 · 𝑛 = 180° · (𝑛 − 2))

Как найти градусную меру угла в многоугольнике. (𝛼 _𝑛 =     ^°·(𝑛_𝑛     ⁾)

7.  Домашнее задание. п.105. №1081, 1083. (слайд 12).

8.  Рефлексия.

Оцените свою активность.

На уроке я:

а) активно работал(а);

б) работал(а), но не активно;

в) был(а) пассивен(на).

Оцените ваше настроение по пятибалльной шкале

1- отвратительное

2  - безразличное

3  - нормальное

4  - хорошее 5 - отличное

свой ответ _

                 1.                                                                                                                               3.

Слайд 2.                                                                                                                  Слайд 4.

                                              

 

                   5.                                                                                                                               7.

Слайд 6.                                                                                                                    Слайд 8.

 

                                                                                                                  

                   9.                                                                                                                              11.

Слайд 10.                                                                                                                  Слайд 12.

 

                                                                                                                

13.