ПРЕДСТАВЛЕНИЕ ДРОБНЫХ ЧИСЕЛ.docx

ПРЕДСТАВЛЕНИЕ ДРОБНЫХ ЧИСЕЛ*

В отличие от хранения целых чисел, для чисел с дробной частью требуется хранить не только двоичное представление числа и его знак, но и позицию разделительной точки. Общепринятым способом хранения дробей является представление с плавающей точкой.

Двоичная нотация с плавающей точкой. Для представления дробных значений используют способ, который называ- ется двоичной нотацией с плавающей точкой (floating-point notation). На рис. 1.15 представлены компоненты дробного чис- ла, состоящего из 8 бит и записанного в двоичной нотации с плавающей точкой (несмотря на то, что в машинах обычно ис- пользуются более длинные битовые комбинации, восьмиразрядный формат достаточно наглядно демонстрирует используе- мые принципы без ненужной избыточности длинных битовых комбинаций).

Пример. Представить битовую комбинацию 01101011, записанную в двоичной нотации с плавающей точкой в деся- тичном формате.

Знаковый бит этого числа равен 0, поле порядка числа имеет значение 110, а поле мантиссы — значение 1011. Вначале выделим мантиссу и поместим плавающую точку слева от нее, как показано ниже:

.1011

Далее выделим значение в поле порядка числа (110) и интерпретируем его как целое трехразрядное число, записанное в двоичной нотации с избытком. Таким образом, в поле порядка числа закодировано целое число 2. Это означает, что плаваю- щую точку в полученном ранее значении следует переместить на два бита вправо (при отрицательном порядке плавающая точка перемещается влево), после чего будет получен окончательный результат:

10.11

Это значение является двоичным представлением числа 2³/₄. Наконец, определяем, что представляемое число является положительным, поскольку знаковый бит имеет значение 0.

Таким образом, мы установили, что битовая комбинация 01101011 в двоичной нотации с плавающей точкой представ- ляет число 2³/₄.

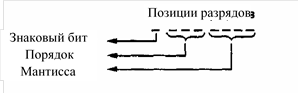Рис. 1.15. Компоненты числа в двоичной нотации с плавающей точкой

Пример. Представить битовую комбинацию 10111100, записанную в двоичной нотации с плавающей точкой в деся- тичном формате.

Выделив мантиссу, получим следующее значение:

.1100

Теперь перенесем плавающую точку на один бит влево, так как в поле порядка содержится значение 011, представляю- щее число –1. Поэтому окончательный вид закодированного двоичного числа будет следующим:

0.01100

Это двоичное число имеет значение ³/₈. Закодированное в значении байта число является отрицательным, поскольку его знаковый бит равен 1. Из этого следует, что битовая комбинация 10111100 в двоичной нотации с плавающей точкой пред- ставляет число – ³/₈.

Для представления чисел в двоичной нотации с плавающей точкой необходимо следовать описанному выше процессу, но уже в обратном порядке.

Пример. Представить в двоичной нотации с плавающей точкой число 1¹/₈.

Сначала число 1¹/₈ необходимо записать в его двоичном представлении: 1.001. Затем эта битовая комбинация копирует- ся в поле мантиссы слева направо, начиная с самой левой единицы в двоичном представлении числа:

_ _ _ _ 1 0 0 1

Определим число разрядов, а также направление, в котором будет перемещаться плавающая точка для получения ис- ходного значения двоичного числа. Здесь можно увидеть, что точка в комбинации .1001 должна быть перемещена на один бит вправо; в результате будет получено исходное значение 1.001. Таким образом, порядок числа равен 1 или 101 в двоичной нотации с избытком четыре. Окончательное значение в байте будет выглядеть следующим образом:

0 1 0 1 1 0 0 1

При заполнении поля мантиссы имеется один тонкий момент: правило требует копировать битовую комбинацию дво- ичного представления числа в поле мантиссы слева направо, начиная с крайней левой единицы. Данное правило исключает возможность различного представления одного и того же значения, и, кроме того (что является, пожалуй, самым важным), если "плавающая" точка расположена в мантиссе перед первой значащей цифрой (т.е. если используется нормализованная запись числа – см. Приложение А), то при фиксированном количестве разрядов, отведенных под мантиссу, обеспечивается запись максимального количества значащих цифр числа, т.е. максимальная точность представления числа в машине.

Пример. Представить в двоичной нотации с плавающей точкой число ³/₈. Двоичным представлением числа ³/₈ является битовая комбинация .011. В этом случае мантисса должна иметь следующее значение:

_ _ _ _ 1 1 0 0

Любой другой вариант, например представленный ниже, недопустим:

_ _ _ _ 0 1 1 0

Ошибка усечения. При операциях с числами, записанными в двоичной нотации с плавающей точкой, могут возникать ошибки, аналогичные ошибкам переполнения.

Пример. Представить число 2⁵/₈ в виде однобайтового кода в двоичной нотации с плавающей точкой.

Прежде всего, определим двоичное представление числа 2⁵/₈, которое имеет вид 10.101. Однако при копировании этого значения в поле мантиссы имеющихся четырех разрядов оказывается недостаточно и самая правая единица в двоичном представлении, имеющая весовое значение ¹/₈, теряется (рис. 1.16). Если не обратить на это внимание и продолжить запол- нение поля порядка числа и знакового бита, будет получена комбинация 01101010, которая на самом деле представляет чис- ло 2¹/₂, а не 2⁵/₈.

Это явление называется ошибкой усечения (truncation error), или ошибкой округления (round-off error). Оно означает, что некоторая часть кодируемого числа теряется, поскольку размер поля мантиссы оказывается недостаточным.

Во избежание подобных ошибок можно использовать поле мантиссы большего размера. Как и в случае целых чисел, для представления значений в нотации с плавающей точкой принято использовать комбинации не менее 32 бит, а не 8 бит, как в приведенных выше примерах. Одновременно это позволяет расширить и размер поля порядка числа. Но даже при ис- пользовании более длинных полей достигаемая точность представления числовых значений в некоторых случаях оказывает- ся недостаточной.

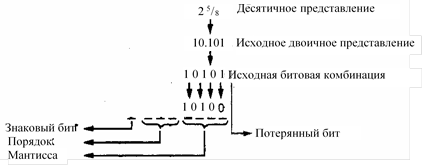
1.16. Схема кодирования числа 2⁵/₈

Существует еще одна причина появления ошибок усечения, с которой каждый из нас уже встречался при изучении десятичной системы счисления. Это проблема бесконечного количества дробных знаков в представлении числа, которая встречается, напри- мер, при выражении числа ¹/₃ в виде десятичной дроби. Дело в том, что некоторые числа невозможно точно выразить, сколько бы цифр мы не использовали для их представления.

Это проблема бесконечного количества дробных знаков в представлении числа, которая встречается, например, при вы- ражении числа ¹/₃ в виде десятичной дроби. Дело в том, что некоторые числа невозможно точно выразить, сколько бы цифр мы не использовали для их представления.

Различие между традиционной десятичной системой счисления и двоичной системой состоит в том, что в двоичной системе больше чисел имеют бесконечное представление, чем в десятичной. Например, даже такое число, как одна десятая, имеет в двоичной системе бесконечное представление. Попробуйте представить себе, какие могут возникнуть проблемы, если какой-либо неосторожный человек решит использовать двоичные числа с плавающей точкой для хранения и обработки данных, представляющих собой суммы в долларах и центах. Например, если единицей измерения данных является доллар, то оказывается невозможным точно представить даже обычную десятицентовую монету. Хорошее решение в подобном слу- чае – измерять данные в единицах центов, тогда все значения окажутся целыми числами, и их можно будет представить с по- мощью двоичного дополнительного кода.

Ошибки усечения могут возникнуть и при сложении очень больших и маленьких чисел. В типичном приложении элек-

тронных таблиц корректные результаты могут быть достигнуты, если различия между суммируемыми значениями не пре- восходят 10¹⁶ или меньше. Поэтому если потребуется добавить единицу к числу

10 000 000 000 000 000,

то велика вероятность, что будет получен ответ

10 000 000 000 000 000

вместо предполагаемого значения

10 000 000 000 000 001.

Пример. Сложить следующие три числа, представленные в однобайтовых кодах двоичной нотации с плавающей точ- кой 2¹/₂ + ¹/₈ + ¹/₈.

Если суммировать эти числа в указанном порядке, то сначала будет получено промежуточное значение 2⁵/₈ (в результа- те сложения чисел 2¹/₂ и ¹/₈), двоичным представлением которого является битовая комбинация 10.101. Это число не может быть представлено точно (см. предыдущий пример), поэтому в результате сложения будет получено число 2¹/₂ (т.е. первое из слагаемых). Если теперь прибавить к полученному результату следующее число ¹/₈, то опять возникнет та же ошибка усече- ния и вновь будет получен тот же неверный ответ – 2¹/₂.

А теперь попробуем сложить те же числа, но в обратном порядке. Сначала сложим числа ¹/₈ и ¹/₈, в результате чего по- лучим число ¹/₄, двоичным представлением которого является битовая комбинация 0.01; соответствующий байт результата будет иметь вид 00111000, отражающий точное значение. Теперь прибавим число ¹/₄ к следующему числу в списке, 2¹/₂. В результате будет получено правильное значение 2³/₄, которое может быть точно представлено в байте в виде кода 01101011. На этот раз ответ правильный.

Поэтому общее правило суммирования большого количества чисел требует начинать операцию сложения с самых ма- лых чисел, предполагая, что в результате будет получено достаточно большое промежуточное значение, которое затем мож- но безопасно сложить с оставшимися большими числами.

Вопросы для самопроверки

1.   Декодируйте приведенные ниже битовые комбинации с помощью формата с плавающей точкой, описанного в этом разделе.

а) 01001010; б) 01101101; в) 00111001; г) 11011100; д) 10101011.

2.   Представьте приведенные ниже числа в формате с плавающей точкой, описанном выше в этом разделе. Укажите на случаи появления ошибок усечения.

а) 2³/₄; б) 5¹/₄; в) ³/₄; г) –3¹/₂; д) –4³/₄.

3.   При использовании формата с плавающей точкой, описанного выше в этом разделе, какая из битовых комбинаций, 01001001 или 00111101, представляет большее числовое значение? Опишите простейшую процедуру определения, какое из двух представленных в этом формате чисел является большим.

4.  Какое наибольшее число может быть представлено в формате с плавающей точкой, описанном выше в этом разделе? Какое наименьшее положительное число может быть представлено в этой системе?