ПРЕДСТАВЛЕНИЕ ЦЕЛЫХ ЧИСЕЛ.docx

ПРЕДСТАВЛЕНИЕ ЦЕЛЫХ ЧИСЕЛ

В разделе рассматриваются две системы двоичного представления (binary notation) целых чисел, которые наиболее час- то используются в компьютерном оборудовании. В основе этих представлений лежит двоичная система счисления, о кото- рой говорится в приложении А, но они обладают некоторыми особенностями, которые делают их более подходящими для вычислительной машины. Одна из этих особенностей дает возможность кодирования и положительных, и отрицательных чисел. Другой особенностью является использование фиксированного числа битов для представления числового значения. Эта особенность может приводить при вычислениях к ошибкам особого рода, обсуждаемым в данном разделе.

Для хранения дробей используется своя система представления, которая дополнительно позволяет закодировать поло- жение точки в дробном числе. Особенности представления дробных чисел описываются в следующем разделе.

Двоичный дополнительный код. Наиболее распространенной системой представления целых чисел в современных компьютерах является представление в двоичном дополнительном коде (two's complement notation). Эта система использует фиксированное число битов для представления числового значения. В современном оборудовании принято использовать представление, при котором каждому значению отводится 32 бита. Такой подход позволяет хранить большой диапазон чи- сел, однако его очень трудно изобразить наглядно. Поэтому мы сосредоточим наше внимание на коротких системах пред- ставления.

а)                                                                   б)

Рис. 1.11. Схемы кодирования в двоичном дополнительном коде

Два представления в двоичном дополнительном коде изображены на рис. 1.11. В этих вариантах для представления чи- сел используются три и четыре бита, соответственно. Построение подобной системы начинается с записи строки нулей, ко- личество которых равно числу используемых двоичных разрядов. Далее ведется обычный двоичный отсчет до тех пор, пока не будет получено значение, состоящее из единственного нуля, за которым следуют лишь единицы. Полученные комбина- ции будут представлять положительные числа 0, 1, 2, 3, Для представления отрицательных чисел выполняется обратный

отсчет, начиная со строки из всех единиц соответствующей длины. Обратный счет продолжается до тех пор, пока не будет получена строка, состоящая из одной единицы, за которой будут следовать все нули. Полученные комбинации будут пред- ставлять числа –1, –2, –3, ... .

Для преобразования битовых комбинаций, представляющих положительные и отрицательные числа, имеющие одно и то же значение по модулю, достаточно копировать исходную комбинацию справа налево до тех пор, пока не будет встречена единица, а затем последовательно заменять значения оставшихся битов их дополнениями (рис. 1.12). Дополнением двоичной ком-

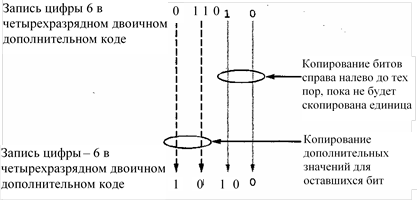бинации (complement) называется такая комбинация, которая получается в результате изменения всех нулей в исходном зна- чении на единицы, а всех единиц на нули. Например, двоичные комбинации 0110 и 1001 являются дополнениями друг другу.

Рис. 1.12. Представление числа –6 в четырехразрядном дополнительном коде

Рассмотрим пример преобразования значений этого кода в десятичное представление.

Пример. Определить десятичное значение комбинации 1010.

Прежде всего, отмечаем, что это значение является отрицательным, так как исходная комбинация содержит единицу в знаковом бите. Затем исходная комбинация преобразуется в комбинацию 0110, которая представляет собой двоичное число

6. Теперь можно сделать окончательное заключение, что исходная двойная комбинация представляет число –6.

Сложение в двоичном дополнительном коде. Для сложения чисел в двоичном дополнительном коде применяется та- кой же алгоритм, как для двоичного сложения, только в этом случае все коды, включая результат операции, будут иметь одинаковую длину. Это означает, что, если в результате сложения появляется дополнительный бит с левого края, он будет отсечен. Именно поэтому 0101 и 0010 в сумме дают 0111, а сумма 0111 и 1011 равна 0010 (0111 + 1011 = 10010, которая усе-

кается до 0010).

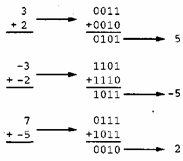На рис. 1.13 представлены примеры сложения чисел в двоичном дополнительном коде. Обратите внимание, что за счет преобразования исходных данных в двоичные до- полнительные коды можно вычислить результат, как для сложения и вычитания, с по- мощью одного и того же алгоритма сложения. Таким образом, основным преимущест- вом двоичного дополнительного кода является то, что операция сложения для любых целых чисел со знаком осуществляется с помощью одного и того же алгоритма.

Поэтому при использовании двоичного дополнительного кода необходимо реали- зовать электронные схемы только для осуществления операций сложения и отрицания (операция вычитания 7 – 5 аналогична операции сложения 7 + (–5)). Этого будет доста- точно для выполнения как операций сложения, так и вычитания. Электронные схемы сложения и отрицания представлены в приложении Б.

Ошибка переполнения. Одной из проблем, которые существуют в любом пред- ставлении в двоичном дополнительном коде, является ограничение на размер чисел, представимых данным количеством битов. Например, если мы используем 4-битовый

Рис. 1.13. Сложение чисел

в двоичном дополнительном коде

двоичный дополнительный код, то у числа 9 не будет соответствующей записи. Это означает, что мы не получим правильно- го ответа, выполнив операцию сложения 5 + 4. На самом деле мы получим ответ – 7. Такая ошибка называется переполнени- ем (overflow), она возникает тогда, когда нужно сохранить число, не попадающее в диапазон чисел, которые могут быть представлены в двоичном дополнительном коде.

Переполнение может возникнуть, когда нужно сложить два положительных или два отрицательных числа. В обоих слу- чаях можно проверить, есть ли ошибка, посмотрев на знаковый разряд полученного результата, т.е. переполнение возникло, если сумма двух положительных чисел имеет код отрицательного числа или сумма двух отрицательных чисел имеет код по- ложительного числа.

В настоящее время для хранения чисел в двоичном дополнительном коде обычно применяются битовые комбинации длиной 32 бита, что позволяет без возникновения переполнения обрабатывать числа от –2 147 483 648 до 2 147 483 647. Если же требуется обработка чисел, превышающих это значение, можно использовать более длинные битовые комбинации или же просто изменить применяемую единицу измерения (например, километры, а не метры).

Двоичная нотация с избытком*. Другой способ представления целочисленных значений называется двоичной нота- цией с избытком (excess notation). В отличие от двоичного дополнительного кода в этой нотации отрицательные числа пред- ставляются комбинациями со знаковым битом, равным 0, а положительные числа – комбинациями со знаковым битом, рав- ным 1 (см. рис. 1.14).

Таблица кодов, изображенная на рис. 1.14, б, называется двоичной нотацией с избытком восемь. Для того чтобы понять, почему это так, сначала переведем коды из таблицы в десятичную систему счисления,как обычный двоичный код, и сравним полученные значения со значениями в таблице.

Рис. 1.14. Схемы кодирования в двоичной нотации с избытком

В каждом случае вы обнаружите, что полученный результат превосходит код в представлении с избытком на восемь. На- пример, последовательность 1100 в двоичной системе является записью числа 12, но в представлении с избытком она явля- ется кодом 4; последовательность 0000 в двоичной системе является записью числа 0, а в представлении с избытком – кодом

8.   Точно так же 5-битовое представление с избытком будет называться представлением с избытком 16, так как, например, последовательность 10000 будет кодом 0, а не 16, как в двоичной записи. Вы можете убедиться, что 3-битовое представление с избытком является представлением с избытком четыре (рис. 1.14, а).

Вопросы для самопроверки

1.  Преобразуйте каждое представленное ниже значение в двоичном дополнительном коде в десятичный формат: а) 00011; б) 01111; в) 11100; г) 11010; д) 00000; е) 10000.

2.   Преобразуйте каждое представленное ниже десятичное значение в двоичный дополнительный код длиной восемь

бит:

а) 6; б) 26; в) 217; г) 13; д) 21; е) 0.

3.   Предположим, что приведенные ниже комбинации битов представляют числа в двоичном дополнительном коде. За-

пишите представление обратных им значений в этом же коде.

а) 00000001; б) 01010101; в) 11111100; г) 11111110; д) 00000000; е) 01111111.

4.  Предположим, что числа в машине сохраняются в двоичном дополнительном коде. Какое наибольшее и наименьшее число может быть записано, если используются битовые комбинации следующей длины:

а) четыре; б) шесть; в) восемь.

5.  В следующих задачах каждая битовая комбинация представляет число, записанное в двоичном дополнительном коде. Вычислите все операции сложения, а затем проверьте ваши результаты посредством преобразования исходных текстов задач в десятичную систему и вычисления их ответов.

а) + 0101 ; б) + 0011 ; в) + 0101 ; г) + 1110 ; д) + 1010 .

0010

0001

1010

0011

1110

6.  Решите следующие задачи с числами в двоичном дополнительном коде, однако на этот раз следите за переполнением и укажите неверные ответы, полученные в результате этой ошибки.

а) + 0100 ; б) + 0101 ; в) + 1010 ; г) + 1010 ; д) + 0111 .

0011

0110

1010

0111

0001

7.   Переведите все приведенные ниже задачи из десятичного представления в четырехразрядный двоичный дополни- тельный код, а затем преобразуйте их в эквивалентные задачи сложения (как это сделала бы машина) и выполните операции суммирования. Проверьте полученные ответы с помощью преобразования их в десятичное представление.

а) + 6 ; б) - 3 ; в) - 4 ; г) + 2 ; д) -1 .

8.   Может ли возникнуть ошибка переполнения при сложении двух чисел в дополнительном коде, если одно из сумми- руемых чисел будет положительным, а другое – отрицательным? Поясните ваш ответ.

9.  Преобразуйте приведенные ниже комбинации битов в двоичной нотации с избытком восемь в десятичный формат, не прибегая к помощи приведенной выше таблицы.

а) 1110; б) 0111; в) 1000; г) 0010; д) 0000; е) 1001.

10.  Преобразуйте приведенные ниже десятичные числа в коды двоичной нотации с избытком восемь без помощи при- веденной выше таблицы.

а) 5; б) –5; в) 3; г) 0; д) 7; е) –8.

11.  Можно ли представить число 9 в двоичной нотации с избытком восемь? А что можно сказать по поводу представле- ния числа 6 в двоичной нотации с избытком четыре? Поясните ваш ответ.