

Числовые множества
На уроке:
• научиться распознавать числовые множнства

Натуральные числа — это целые, положительные числа,
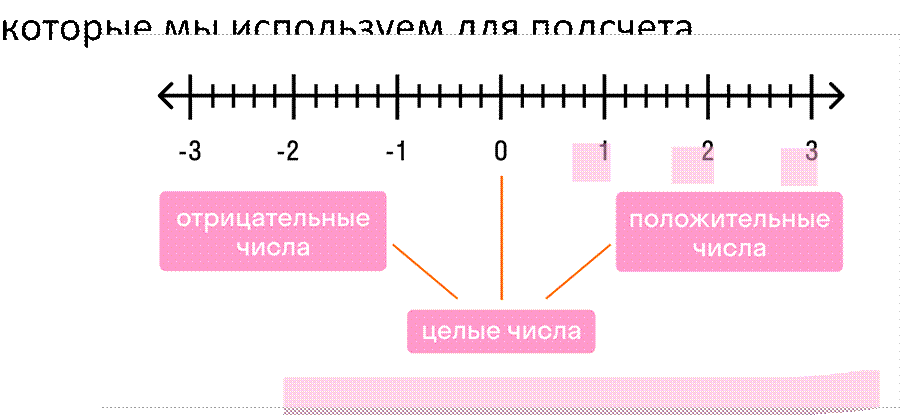 Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 + ∞.
Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 + ∞.
Множество целых чисел обозначают N
Целое число — это натуральное число, а также противоположное ему число и нуль.
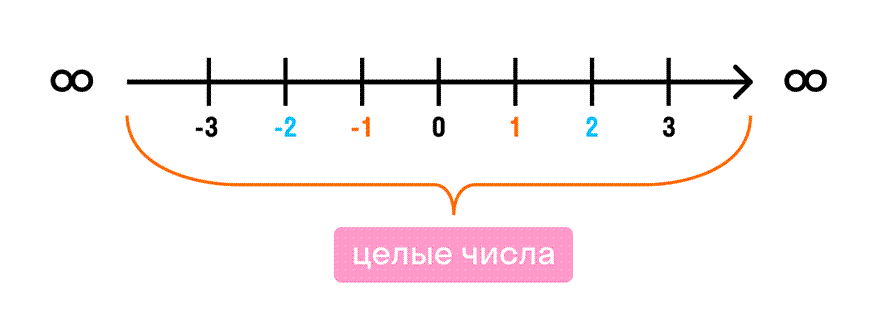
Множество целых чисел обозначают Z
Что важно знать о целых числах:
1. Сумма, разность и произведение целых чисел в результате дают целые числа.
2. Не существует самого большого и самого маленького целого числа. Этот ряд бесконечен.
3. Обыкновенные и десятичные дроби нельзя назвать целыми числами.
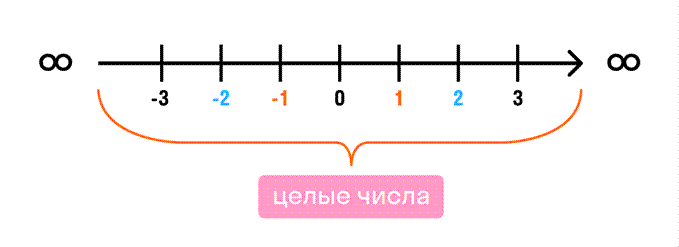
 Последовательность целых чисел можно
записать так:
Последовательность целых чисел можно
записать так:
∞ + ... -4, -3, -2, -1, 0, 1, 2, 3, 4 … + ∞
Последовательность натуральных чисел можно записать так:
0, 1, 2, 3, 4 … + ∞
Рациональные числа - целые и дробные числа вместе
 Обозначения
Обозначения
𝑁 ⊂ 𝑍, 𝑍 ⊂ 𝑄, 𝑁 ⊂ 𝑄
𝑁⊂ 𝑍⊂𝑄
Принадлежность элементов множеству
-5 ∋ Z, 5 ∋ Z
5 ∋ N
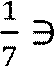 𝑄,
𝑄, 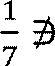 𝑁
𝑁
 Если
элементами множества являются
Если
элементами множества являются
числа, то его называют числовым множеством

20 августа 2024 г.
Мерзляк А.Г. Математика: 6 класс: учебник / А.Г. Мерзляк, В.Б.Полонский, М.С. Якир; под ред. В.Е. Подольскгого.-5-е изд., стереотип.-М.: Вентана-Граф, 2020 Онлайн школа Skysmart: https://skysmart.ru/articles/mathematic/pryamaya-iobratnaya-proporcionalnost
20 августа 2024 г.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.