Приемы формирования умения решения задач на движение

Приемы формирования умения решения задач на движение

В школьном курсе математики широко применяются несколько способов решения текстовых задач:

- арифметический способ;

- алгебраический способ;

- способ подбора;

- графический способ;

- практический способ.

Все способы равноправны, но наиболее универсальными являются алгебраический и арифметический.

Педагоги за период своей работы в школе сталкиваются с тем, что текстовые задачи не всегда понимаемы учениками, поэтому каждый старается помочь ребенку, применяя новые приемы и способы решения текстовых задач. В Таблице 1 рассмотрены способы решения текстовых задач разными педагогами.

Таблица 1

Способы решения текстовых задач

Для обучения методике решения текстовых задач по математике в начальной школе педагогу необходимо использовать различные приемы обучения, которые бы соответствовали развитию логического мышления и творческих способностей детей.

Учащихся следует знакомить с различными методами решения текстовых задач: арифметическим, алгебраическим, геометрическим, логическим и практическим; с различными видами математических моделей, лежащих в основе каждого метода; а также с различными способами решения в рамках выбранного метода. 

Решение текстовых задач дает богатый материал для развития и воспитания учащихся. Краткие записи условий текстовых задач – примеры моделей, используемых в начальном курсе математики. Метод математического моделирования позволяет научить школьников: 
а) анализу (на этапе восприятия задачи и выбора пути реализации решения); 

б) установлению взаимосвязей между объектами задачи, построению наиболее целесообразной схемы решения; 

в) интерпретации полученного решения для исходной задачи;

г) составлению задач по готовым моделям и др. 

Математика – это орудие для размышления, в ее арсенале имеется большое количество задач, которые на протяжении тысячелетий способствовали формированию мышления людей, умению решать нестандартные задачи, с честью выходить из затруднительных положений. 

К тому же воспитание интереса младших школьников к математике, развитие их математических способностей невозможно без использования в учебном процессе задач на сообразительность, задач-шуток, математических фокусов, числовых головоломок, арифметических ребусов и лабиринтов, дидактических игр, стихов, задач-сказок, загадок и т.п. 

Основной метод решения текстовых задач в начальной школе – арифметический. Большинство действующих программ для начальной школы не ставят своей целью формирование у школьников умений решать текстовые задачи геометрическим методом, хотя он широко используется для построения вспомогательных моделей в ходе решения задач различных видов.

В последнее время арсенал учителя начальных классов пополнился учебниками математики, в которых предусмотрено ознакомление учащихся с этим методом решения задач. Так, в учебниках Л.Г. Петерсон приводятся задачи «на движение», решение которых осуществляется с использованием либо конструктивного приема, либо графико-вычислительного – основными приемами геометрического метода решения текстовых задач.

Использование геометрического метода в курсе начальной школы позволяет разнообразить работу по решению задач, способствует ознакомлению учащихся с методом математического моделирования, развивает логическое мышление и познавательный интерес детей. Подробно с этим методом решения текстовых задач и его применениями можно познакомиться в работах, которые приведены в конце статьи.

Приведем подборку задач, которые, на наш взгляд, расширяют границы применения геометрического метода в начальной школе и являются дополнением к системе задач, предложенных в некоторых федеральных комплектах учебников математики для начальных классов. К тому же эти задания может использовать учитель, работающий по любой системе обучения, на внеклассных занятиях. В каждом примере приводится возможный вариант беседы учителя с классом.

Пример 1. Ознакомление учащихся с построением графика движения.

Задача. Петя вышел из города A по шоссе со скоростью 4 км/ч. На каком расстоянии от города A будет мальчик через 5 часов?

– Покажите движение мальчика с помощью числового луча (рис. 1)

Рис. 1

– На каком расстоянии от города A Петя будет через 5 часов с момента его выхода? (20 км.)

– Какую величину мы откладывали на числовом луче при решении задач на движение? (Расстояние.)

– А как вы узнали, на каком расстоянии от пункта A будет находиться мальчик через 5 часов? (4 · 5 = 20.)

– Сегодня мы познакомимся с другим методом решения таких задач на движение. Построим горизонтальную прямую. Отметим на ней начало координат – точку О, как в предыдущем случае. Назовем ее ось Ox. На ней будем откладывать время движения мальчика. Выберем единичный отрезок, равный 1 часу. Чтобы отразить на чертеже зависимость между временем и расстоянием, нам понадобится еще и вертикальная ось. Проведем через точку О вертикальную ось. Назовем ее ось Oy. На ней будем откладывать расстояние, пройденное мальчиком. Выберем единичный отрезок, равный 1 км. Начало движения Пети обозначим точкой A(0; 0).

Рис. 2

– Что известно в задаче о движении мальчика? (Он вышел из города A со скоростью 4 км/ч.)

– Поясните, как вы понимаете фразу «вышел со скоростью 4 км/ч». (За 1 час мальчик проходит 4 км.)

– Покажите на оси времени (оси Ox) точку, координата которой 1 ч.

– А теперь на оси расстояния (оси Oy) покажите точку, координата которой 4 км.

– Точка (1; 4) показывает, что Петя за 1 час прошел 4 км. Отметим ее.

– Мальчик движется по прямой. Через найденную нами точку и точку, показывающую начало его движения, проведем прямую. Это и есть график движения мальчика (рис. 2).

– Попробуйте теперь самостоятельно ответить на вопрос задачи. Найдите точку на графике, которая поможет определить, на каком расстоянии от города А будет находиться мальчик через 5 часов после начала его движения. (Точка M.)

– Можно ли по графику узнать, за какое время Петя пройдет 8 км, 12 км и т.д.?

Пример 2. Ознакомление учащихся с построением графика движения объекта, скорость которого изменяется в процессе движения.

Задача. Из пункта А в пункт В вышел пешеход. Первые 2 часа он шел со скоростью 4 км/ч, затем один час со скоростью 2 км/ч и оставшиеся 3 часа – со скоростью 6 км/ч. Найти расстояние между пунктами А и В.  На каком расстоянии от пункта А пешеход был через 6 часов?

– Отметим точку А(0; 0). Построим график движения пешехода за первые 2 часа его движения. (За 1 час он про2 шел 4 км, за 2 часа – 8 км.)

Отметим точку С(2; 8) и соединим ее с точкой А (рис. 3).

Рис. 3

– Что известно о дальнейшем движении пешехода? (Следующий час он шел со скоростью 2 км/ч.)

– Построим график движения пешехода в следующий час его движения. Из какой точки будем продолжать строить этот график? (Из точки С.)

– Почему из точки С? (Пешеход продолжает двигаться, только с другой скоростью.)

– За следующий час пешеход пройдет 2 км, значит, он будет находиться от точки А на расстоянии 10 км (8 км + 2 км). К этому времени он будет находиться в пути 3 часа. Отметим точку (3; 10). Обозначим эту точку буквой D(3; 10). Соединим точки С и D.

– Пешеход шел еще 3 часа со скоростью 6 км/ч. Построим график движения пешехода за это время.

– За 1 час пешеход прошел еще 6 км, за 3 часа – 18 км, т.е. он будет находиться от точки А на расстоянии 28 км (10 км + 18 км). К этому времени он будет находиться в пути 6 часов. Отметим точку М(6; 28). Следовательно, расстояние между пунктами A и B равно 28 км.

Пример 3. Решение задач на встречное движение с одновременным выходом.

Задача. Отец выехал из села в город на автобусе, одновременно навстречу ему из города в село на велосипеде выехал сын. Между городом и селом расстояние 300 км. На каком расстоянии от села и через какое время произойдет их встреча, если скорость автобуса 60 км/ч, а велосипедиста 15 км/ч? На доске построен график (рис. 4а).

– Что изображено на графике? (Движение автобуса.)

– Почему? (На графике показано, что за 1 час пройдено расстояние 60 км, т.е. скорость движения – 60 км/ч, а это скорость автобуса.)

– Что обозначает точка A? (Начальный пункт, из которого выехал отец, – село.)

– Построим график движения велосипедиста.

– Что нам известно о движении велосипедиста? (Он ехал в село из города, т.е. навстречу отцу; его скорость – 15 км/ч.)

– Из какой точки будем строить график его движения? (Из точки В.)

Рис. 4

– Почему? (Велосипедист и автобус движутся навстречу друг другу; выехали они в одно и то же время, значит, точка, из которой мы начнем строить график движения велосипедиста, лежит на одной вертикальной прямой с точкой А; расстояние между городом и селом 300 км, ищем точку (0; 300) – это точка В.)

– Что еще необходимо учитывать при построении графика движения? (Скорость движения.)

– Какова же скорость движения велосипедиста? (15 км/ч.)

– А зачем нам нужна скорость движения? (Для того, чтобы определить расстояние, которое проехал сын за 1 час, – 15 км.)

– Итак, спустя 1 час велосипедист находился на расстоянии 15 км от точки В, т.е. на расстоянии 285 км от точки А. Отмечаем на графике точку (1; 285) и проводим прямую через эту точку и точку В(0; 300). Тем самым мы построим график движения сына на велосипеде. Точка пересечения обоих графиков движения – место встречи отца и сына. Обозначим ее буквой М.

– Чтобы узнать, на каком расстоянии от А и через какое время произошла встреча, проведем из точки М прямые под прямым углом к осям Ох и Оу. Видим, что точка M имеет координаты (4; 240).

– На каком расстоянии от села произойдет встреча отца и сына? (На расстоянии 240 км.)

– Через какое время после начала движения произойдет встреча?

(Встреча произойдет через 4 часа.)

Пример 4. Решение задачи «на движение вдогонку».

Задача. Из города А со скоростью 5 км/ч вышел Ваня. Спустя 3 часа в том же направлении из города А выехал Женя на велосипеде со скоростью 10 км/ч. Через какое время Женя догонит Ваню?

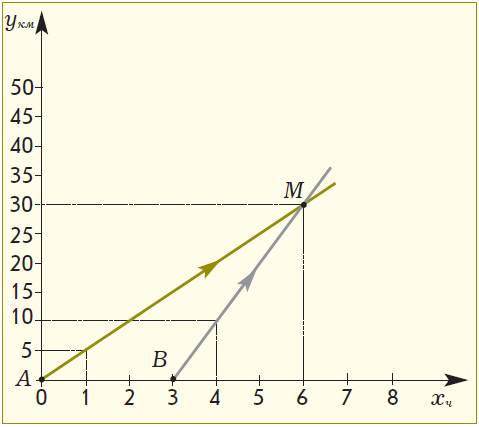 Рис.5

– Построим график движения Вани (на графике он изображен цветной

линией, рис. 5).

– Построим график движения Жени.

– Что нам известно о движении Жени? (Он ехал из того же города и в том же направлении со скоростью 10 км/ч.)

– Из какой точки будем строить график его движения? (Из точки B

(3; 0).)

– Почему? (Женя выехал из города А, значит, точка, из которой мы начнем строить график его движения лежит на одной горизонтальной прямой с точкой А. Женя выехал на 3 часа позже Вани, ищем точку (3; 0) – это точка В.)

– Что еще необходимо учитывать при построении графика движения? (Скорость движения.)

– Какова же скорость движения Жени? (10 км/ч.)

– Значит, через 1 час после начала идвижения Жени прошло 4 часа от начала движения Вани. Отмечаем на графике точку (4; 10) и проводим прямую через эту точку и точку B.

– Мы построили график движения Жени. Точка пересечения графиков движения – место, в котором Женя догонит Ваню. Обозначим ее буквой М. Определяем, что точка M имеет координаты (6; 30). Следовательно, Женя догонит Ваню через 6 часов после начала движения Вани на расстоянии 30 км от города A.

Пример 5. Решение задачи различными способами (с использованием графика и диаграммы).

Задача. Из пункта А в пункт В выехал велосипедист со скоростью 10 км/ч. Одновременно с ним из пункта В в пункт А вышел пешеход со скоростью 5 км/ч. Через какое время произойдет их встреча, если расстояние от А до В составляет 75 км?

На доске дано графическое решение задачи (рис. 6).

– Что изображено на доске? (Решение задачи.)

– Что показывает цветная линия? (График движения велосипедиста.)

– Что показывает серая линия? (График движения пешехода.)

– Почему серая линия выходит из точки В? (Пешеход и велосипедист движутся навстречу друг другу, движение начинают одновременно.)

– Что означает точка М? (Момент встречи пешехода и велосипедиста.)

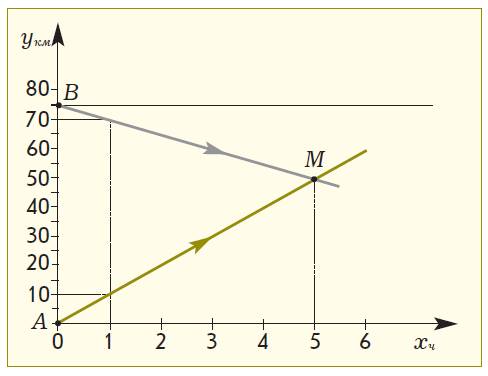
Рис. 6

– Решить эту задачу можно, построив диаграмму. Велосипедист движется из пункта А. За первый час велосипедист проехал 10 км; проведем цветной вертикальный отрезок длиной 10 км из точки (1; 0) вверх (рис. 7).

Пешеход движется навстречу велосипедисту из пункта В. За первый час пешеход прошел 5 км; проведем вертикальный отрезок серого цвета длиной 5 км из точки (1; 75) вниз.

Велосипедист за два часа проехал 20 км; проведем цветной вертикальный отрезок длиной 20 км из точки (2; 0) вверх. За два часа пешеход прошел 10 км; проведем вертикальный отрезок серого цвета длиной 10 км из точки (2; 75) вниз.

Рис.7

Велосипедист за три часа проехал 30 км; проведем цветной вертикальный отрезок длиной 30 км из точки (3; 0) вверх. За три часа пешеход прошел 15 км; проведем вертикальный отрезок серого цвета длиной 10 км из точки (3; 75) вниз.

Продолжите построение диаграммы. Что вы заметили? (Цветной и серый отрезки «встретились» через 5 часов.)

– Что это означает? (Пешеход и велосипедист встретились через 5 часов.)