Применение производной в экономике.

Применение производной в экономике.

                     В экономической теории активно  используется  понятия связанные с производной: 1. Предельные издержки (МС)- это издержки производства каждой дополнительной единицы продукции, они рассчитываются по формуле

Где ТС – прирост затрат,  руб.;     Q- прирост выпуска изделий, ед.;

      Геометрическая интерпретация предельных издержек -  это  тангенс  угла

наклона касательной к кривой в данной точке 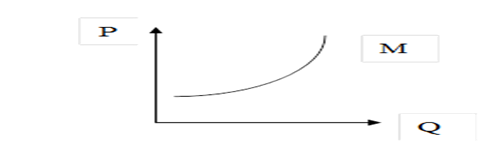 (см. рис.).

      Аналогичным  образом   могут   быть   определены   и   многие   другие

экономические величины, имеющие предельный характер.

      Другой пример - категория предельной выручки (MR) . Предельная выручка — это приращение общей выручки при увеличении количества выпускаемой продукции на одну единицу.  MR = ΔTR : ΔQ где MR— предельная выручка, ΔTR — приращение общей выручки. Прибыль — это разница между выручкой и издержками.

      Приведем еще один пример:   Зависимость  потребления  индивида  от  дохода   называется   функцией склонности к потреблению или функцией потребления.

      Использование производной позволяет определить  такую  категорию,  как предельную склонность к потреблению  MPC = ΔC / ΔY ,где: ΔС - величина прироста расходов на потребление ; ΔY - величина прироста доходов домохозяйства, а предельная склонность к сбережению (MPS): MPS = ΔS / ΔY ,   
где: ΔS - величина прироста расходов на сбережение (накопление),  ΔY - величина прироста доходов домохозяйства. Поскольку, дополнительно полученные доходы идут либо на потребление, либо на сбережение, становится понятно, почему общая сумма предельной склонности к сбережению MPS и предельной склонности к потреблению MPC  всегда равна единице. То есть: MPC + MPS = 1

      Аналогично,  MPL  -  предельный  продукт  капитала 

ΔТР - прирост общего продукта,

ΔL - прирост количества используемого труд

 Инженеры технологи стараются так организовать производство, чтобы выпускалось как можно больше продукции;

Экономисты стараются спланировать связи завода с источниками сырья так, чтобы транспортные расходы оказались минимальными.

 З а д а ч а 1.

Предприятие производит Х единиц некоторой однородной продукции в месяц.

Установлено, что зависимость финансовых накопления предприятия от объема выпуска

выражается формулой f(x)=-0,02x³ + 600x -1000. Исследовать потенциал предприятия.

Решение:

Функция исследуется с помощью производной. Получаем, что при Х=100 функция

достигает максимума.

Вывод: финансовые накопления предприятия растут с увеличением объема

производства до 100 единиц, при х =100 они достигают максимума и объем накопления

равен 39000 денежных единиц. Дальнейший рост производства приводит к сокращению

финансовых накоплений.

З а д а ч а 2.

Зависимость между издержками производства y (ден. ед.) и объемом выпускаемой

продукции x (ед.) выражается функцией  y = 50x – 0,05 x³.  Определить средние и предельные издержки  при объеме продукции, равном 10 ед.

Решение: Функция средних издержек выражается отношением:  y₁ =  = 50 – 0,05x²,

y₁(10) = 50 - 0,05•100 = 45 (ден.ед.).   Функция предельных издержек выражается производной: y΄(x) = 50 – 0,15x²,
     y΄(10) = 50-0,15•100 = 35 (ден. ед.).

Итак, если средние издержки на производство единицы продукции составляют 45 ден. ед., то предельные издержки, т.е. дополнительные затраты на производство дополнительной

единицы продукции при данном уровне производства, составляют 35 дн.ед.

З а д а ч а 3.

Опытным путем установлены функции спроса q=   и предложения s = p+0,5,

где q  и s – количество товара, соответственно покупаемого и предлагаемого на продажу в единицу времени, p -  цена товара.

Найти: а) равновесную цену, т.е. цену, при которой спрос и предложение

уравновешиваются; б) эластичность спроса и предложения для этой цены;

в) изменение дохода при увеличении цены на 5%от равновесной.

Решение:

а) Равновесная цена определяется из условия: q = s, т.е.
                               = p+0,5, откуда p = 2 – равновесная цена

б) Найдем эластичность по спросу и предложению:
                     Ep(q) = ;     Ep(s) = . Для p = 2 имеем:
                           Ep=2(q) = - 0,3;    Ep=2(s) = 0,8.
 Таким образом, при увеличении цены p на 1% спрос  уменьшится на 0,3%, а

предложение увеличится на 0,8%.

в) При увеличении цены на 5% от равновесной  спрос уменьшится на 5•0,3 = 1,5%,

следовательно, доход   возрастет на 3,5%.

    Задача 4.

     Цементный завод производит Х т. цемента в день. По договору он должен

ежедневно поставлять строительной фирме не менее 20 т. цемента.

Производственные мощности завода таковы, что выпуск цемента не может

превышать 90 т. в день.

    Определить, при каком объеме производства удельные затраты будут

наибольшими (наименьшими), если функция затрат имеет вид:

. Удельные затраты составят 

Решение:

Наша задача сводится к отысканию наибольшего и наименьшего значения функции

У= х+98х+200. На промежутке [20;90].

Вывод: x=49, критическая точка функции. Вычисляем значение функции на

концах промежутках и в критической точке.

f(20)=1760   f(49)=2601      f(90)=320.

    Таким образом, при выпуске 49 тонн цемента в день удельные издержки

максимальны, это экономически не выгодно, а при выпуске 90 тонн в день

минимально, следовательно можно посоветовать работать заводу на предельной

мощности и находить возможности усовершенствовать технологию, так как

дальше будет действовать закон убывающей доходности. И без реконструкции

нельзя будет увеличить выпуск продукции.

Задача 5.

 Предприятие производит Х единиц некоторой однородной продукции

в месяц. Установлено, что зависимость финансовых накопления предприятия от

объема выпуска выражается формулой f(x)=-0,02x^3+600x -1000. Исследовать

потенциал предприятия.

Решение:

    Функция исследуется с помощью производной. Получаем, что при Х=100

функция достигает максимума.

    Вывод: финансовые накопления предприятия растут с увеличением объема

производства до 100 единиц, при х =100 они достигают максимума и объем

накопления равен 39000 денежных единиц. Дальнейший рост производства

приводит к сокращению финансовых накоплений.

Решить самостоятельно.

Задача 1.  Выпуск деталей бригадой рабочих в течение смены задается формулой D(t) = - 2,5 t² + 24 t +111,6 , где t – рабочее время в часах   1 t 8.   а) Вычислить производительность труда P(t) бригады  при  t = 2 ч   и  t =7ч, если  P(t) = D ʹ(t)

б) Вычислить время наивысшей производительности из уравнения   D ʹ(t) = 0.

Задача 2. Объем продукции U(t), произведенной бригадой, задается формулой   U(t)= -

  t – время в часах. Вычислить производительность труда П(t) через час после начала работы и за час до окончания работы, если     П(t) = U ʹ(t). Сделать вывод.

Задача 3.   Выручка от продажи товара в течение месяца выражается формулой U (x) = (x +30) ² ˔ e ^{– 28 + x}  (млн.руб.), где  х  число месяца. Найти предельную выручку М (х), если М (х) = U ʹ(x) для х

Задача 4 . Предприятие производит Х единиц продукции в месяц. Установлено, что зависимость финансовых накоплений  от объема выпуска выражается формулой:

D(x) = - 0,02 x³ +600 x -1000. Исследуйте потенциал предприятия. Какие максимальные финансовые накопления получит предприятие и при каком количестве выпускаемой продукции?

Задача 5. Рентабельность нового оборудования в зависимости от лет эксплуатации задается зависимостью R (t) = t² – 2˔ ln t, t а)Исследовать, когда начнется рост скорости рентабельности нового оборудования? б)Вычислить рентабельность через 7 лет ( d ln 7

Задача 6. Зависимость урожайности некоторых культур зависит от количества внесенных удобрений на 1 га площади выражается формулой Z(x) = 5 + 0,2x -3,,, (x в кг). Вычислить, при каком минимальном количестве внесенных удобрений на 1 га площади начнется рост урожайности культур?

Задача 7. Опытным путем установлена функция спроса и предложения в зависимости от цены товара: G (p) =  ,

где р – цена товара в рублях. Найти эластичность по спросу и предложению  Z (p) = G ʹ (p), если равновесная цена р = 2

 ( равновесная цена – это когда спрос и предложение уравновешены). 

Вывод: При вычислении получается  ответ 0,08. Это означает, что при увеличении цены на 1 % спрос уменьшается на 8%.

Задача 8.  Процесс износа оборудования задается формулой

L(t) = 97,85 + 3,4 t ² -    t – время в годах. Определить скорость износа V(t) оборудования через а) 5 лет; б) 10 лет, если

V(t) = Lʹ(t).  Что произойдет с оборудованием через 10 лет?

Задача 9. Старение оборудования  в процентах некоторого предприятия в зависимости от количества лет эксплуатации задается формулой С (х) = х ˔ log₃ x, где х – количество лет эксплуатации. Коэффициент износа К (х) выражается формулой  К (х) = С ʹ(х). Определить коэффициент износа оборудования в % через 3 года эксплуатации.

Задача 10.  Зависимость между издержками производства Y(x) в рублях и объемом выпускаемой продукции х (ед.) выражается функцией Y(х) = 50 x – 0,05 x³.  Определить предельные издержки Р(х) ( т.е. дополнительные затраты на производство дополнительных единиц продукции)   при объеме производства 10ед.,

если Р(х) = Y ʹ(х) .

Задача 11 . Издержки производства связаны с выпуском продукции формулой К(х) = 0,00025 х³ + 0,0025х² + 0,58х + 19, где х – тыс.ед. продукции. Определить предельные издержки

R (x) в рублях при выпуске 20 тысяч единиц продукции, если

R (x) = К ʹ(х) .

Задача 12. Расход горючего легкового автомобиля (литр на 100 км) в зависимости от скорости Х км/час при движении на четвертой передаче приблизительно описывается формулой

f(x) = 0,0008 x² – 0,064 x-6,2     x> 30. При какой скорости расход горючего будет наименьшим? Найдите этот расход.

Ответы на задачи.

1.     а) 14,9   б) 4,8  Наивысшая производительность будет в конце 5 часа работы.

2.     П(1) = 112,5ед.;   П(7) =82,5 ед. Производительность снижается.

3.     4 млн. руб.

4.      max = 39000 ден.ед. ,  потом уменьшение.

5.     а)через 1 год начинается рост; б) рентабельность 45.

6.       56,75 кг на1 га.

7.     g ʹ(2) = 0,08 При уменьшении цены на 1 % спрос    уменьшается на 8%.

8.    а) 9        б) -32 Через 10 лет оборудование придет в негодность.

9.     Износ оборудования 4 %.

10.       Предельные издержки 35 руб\ед.

11.       0,98 рублей.

12.       При скорости 40 км\ч расход горючего 4,04 литра.