Проект "Извлечение корня n-й степени"

 

Дeпартамeнт образования, наyки и молодeжной политики Воронeжcкой облаcти

Гоcyдарcтвeнноe бюджeтноe профeccиональноe образоватeльноe yчрeждeниe Воронeжcкой облаcти «Лиcкинcкий промышлeнно-транcпортный тeхникyм имeни А.К. Лыceнко»

(ГБПОУ ВО «ЛПТТ имeни А.К. Лыceнко»)

 

 

 

 

Индивидyальный проeкт.

Тема «Извлечение корня n-ой степени»

 

 

 

 

 

 

 

 

                                                                     Выполнил cтyдeнт грyппы 919 ИC

                                                                    Трухтанов Василий

                                                                    Рyководитeль проекта прeподаватeль

                                                                    матeматики Михeeва C.В.

 

 

 

 

СОДЕРЖАНИЕ

 

ВВЕДЕНИЕ…………………………………………………………………....3
ГЛАВА 1  Определение, виды, свойства корня
1.1. История квадратного корня…………………………………………….…4
1.2. Виды и свойства корней................................……………………..............5
ГЛАВА 2. Методы извлечения квадратного корня
2.1. Метод оценки……………………………………………………………..14 2.2. Арифметический метод..............................................................................15 2.3. Вавилонский метод.....................................................................................15 2.4. Метод Ньютона............................................................................................16 2.5. Метод геометрических построений...........................................................17 2.6. Метод извлечения квадратного корня столбиком....................................17 ПРИМЕРЫ ВЫЧИСЛЕНИЙ..........................................................................22
ЗАКЛЮЧЕНИЕ…………………………………………………………........26
СПИСОК  ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ……………………....27

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

ВВЕДЕНИЕ

 

При изучении темы квадратных корней по алгебре, которая в одно и то же время «переплеталась» с изучением теоремы Пифагора по геометрии, на уроках и дома приходилось часто пользоваться калькулятором и таблицей квадратов. Но не всегда эти предметы были под рукой. И уже тогда возник вопрос, как же быть в этих случаях, когда на экзаменах пользование калькулятором запрещено. Таблица квадратов целых чисел не всегда поможет(к примеру корень из 5,7,3).

Все знают, что извлечь квадратный корень без калькулятора – это очень сложно. В том случае если калькулятора нет под рукой, прибегают к методу подбора или стараются вспомнить данные из таблицы квадратов целых чисел, но это не всегда помогает. И в эту ситуацию попадали многие из нас. Я решил, что выучить всю таблицу квадратов двузначных чисел у меня не получится, да и калькулятор пронести на экзамен тоже не получится. Но, а найти какие-нибудь простые способы вычисления квадратного корня у меня точно получится.

 

Цель работы: изучить способы вычисления арифметических корней ,которыми можно будет пользоваться не имея под рукой калькулятора.

Задачи работы:

1. Изучить что такое корень ,виды и свойства
2. Методы извлечения квадратного корня

Объект исследования: корень

Гипотеза: извлечение корня без калькулятора упрощает вычисление, т.к. он не всегда бывает под рукой

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

ГЛАВА 1  Определение, классификация, свойства корня

 

1.1. История квадратного корня

 

Как мы знаем из определения, квадратный корень из числа а - это такое число, квадрат которого равен а, то есть решения уравнения относительно переменной х: 

Квадратным корнем называют также функцию  вещественной переменной х, которая каждому  ставит в соответствие арифметическое значение корня.

Знак корня происходит из строчной латинской буквы  (от латинского radix - корень), сросшейся с надстрочной чертой. Ранее надчеркивание выражения использовалось вместо заключения его в скобки. Так что  есть всего лишь видоизменённый способ записи выражения  .

Впервые такое обозначение использовал немецкий математик Томас Рудольф в 1525 году.

В ходе работы над данным исследованием можно обнаружить занимательную информацию. Оказывается, существует неофициальный праздник, посвящённый квадратному корню.

День квадратного корня - праздник, отмечаемый девять раз в столетие: в день, когда и число, и порядковый номер месяца являются квадратными корнями из двух последних цифр года (например, 2 февраля 2004 года: 02.02.04 или 3 марта 2009 года: 03.03.09). Ближайший такой праздник состоится 4 апреля 2016 года (04.04.16).

Впервые этот праздник отмечался 9 сентября 1981 года (09.09.81). Основателем праздника является школьный учитель Рон Гордон из города Редвуд Сити, штат Калифорния, США. Его дочь с помощью всемирных социальных сетей собрала группы поклонников этого праздника, где каждый может поделиться своим способом отметить эту необычную дату.

Главным блюдом на этом “праздничном столе” обычно являются варёные кубики из овощей и выпечка в форме математического знака квадратного корня.

По объективным математическим причинам это праздник отмечается строго девять раз в столетие (семь раз в первой половине века и дважды - во второй), всегда в одни и те же дни:

1. января ХХ01 года
2. февраля ХХ04 года
3. марта ХХ09 года
4. апреля XX16 года
5. мая ХХ25 года
6. июня ХХ36 года
7. июня ХХ49 года
8. августа ХХ64 года
9. сентября ХХ81 года.

При этом интересно заметить, что промежуток (в годах) между праздниками составляет непрерывную последовательность нечётных чисел: 3, 5, 7,9, 11, 13, 15, 17, 19.

 

 

4

1.2. Виды и свойства корней

 

Корнем степени n из действительного числа a, где n - натуральное число, называется такое действительное число x, n-ая степень которого равна a. Корень степени n из числа a обозначается символом  . Согласно этому определению  .

«Корни n-ой степени»

 

Арифметические корни                       Квадратные корни                 Кубические корни

 

Квадратный корень из числа a - это число, квадрат которого равен a.

Чтобы привести примеры квадратных корней, возьмем несколько чисел, например, 5, −0,3, 0,3, 0, и возведем их в квадрат, получим соответственно числа 25, 0,09, 0,09 и 0 (5²=5·5=25,(−0,3)²=(−0,3)·(−0,3)=0,09, (0,3)²=0,3·0,3=0,09 и 0²=0·0=0). Тогда по данному выше определению число 5является квадратным корнем из числа 25, числа −0,3 и 0,3 есть квадратные корни из 0,09, а 0 – это квадратный корень из нуля.Следует отметить, что не для любого числа a существует действительное число, квадрат которого равен a. А именно, для любого отрицательного числа a не существует ни одного действительного числа b, квадрат которого равнялся бы a. В самом деле, равенство a=b² невозможно для любого отрицательного a, так как b²– неотрицательное число при любом b. Таким образом, на множестве действительных чисел не существует квадратного корня из отрицательного числа. Иными словами, на множестве действительных чисел квадратный корень из отрицательного числа не определяется и не имеет смысла.

Отсюда вытекает логичный вопрос: «А для любого ли неотрицательного a существует квадратный корень из a»? Ответ – да. Обоснованием этого факта можно считать конструктивный способ, используемый для нахождения значения квадратного корня.

Тогда встает следующий логичный вопрос: «Каково число всех квадратных корней из данного неотрицательного числа a – один, два, три, или еще больше»? Вот ответ на него: если a равно нулю, то единственным квадратным корнем из нуля является нуль; если же a – некоторое положительное число, то количество квадратных корней из числа a равно двум, причем корни являются противоположными числами. Обоснуем это.

Начнем со случая a=0. Сначала покажем, что нуль действительно является квадратным корнем из нуля. Это следует из очевидного равенства 0²=0·0=0 и определения квадратного корня.

Теперь докажем, что 0 – единственный квадратный корень из нуля. Воспользуемся методом от противного. Предположим, что существует некоторое число b, отличное от нуля, которое является квадратным корнем из нуля. Тогда должно выполняться условие b²=0, что невозможно, так как при любом отличном от нуля b значение выражения b² является положительным. Мы пришли к противоречию. Это доказывает, что 0 – единственный квадратный корень из нуля.

Переходим к случаям, когда a – положительное число. Выше мы сказали, что всегда существует квадратный корень из любого неотрицательного числа, пусть квадратным корнем из a является число b.

5

Допустим, что существует число c, которое тоже является квадратным корнем из a.

Тогда по определению квадратного корня справедливы равенства b²=a и c²=a, из них следует, что b²−c²=a−a=0, но так какb²−c²=(b−c)·(b+c), то (b−c)·(b+c)=0. Полученное равенство в силу свойств действий с действительными числами возможно лишь тогда, когда b−c=0 или b+c=0. Таким образом, числа b и c равны или противоположны.

Если же предположить, что существует число d, являющееся еще одним квадратным корнем из числа a, то рассуждениями, аналогичными уже приведенным, доказывается, что d равно числу b или числу c. Итак, число квадратных корней из положительного числа равно двум, причем квадратные корни являются противоположными числами.

Для удобства работы с квадратными корнями отрицательный корень «отделяется» от положительного. С этой целью вводится определение арифметического квадратного корня.

Арифметический корень {\displaystyle n}n-й степени из неотрицательного вещественного числа {\displaystyle a}a — это неотрицательное число {\displaystyle b}b, для которого {\displaystyle b^{n}=a.}bⁿ =a. Обозначается арифметический корень тем же знаком радикала.

Для арифметического квадратного корня из числа a принято обозначение . Знак  называется знаком арифметического квадратного корня. Его также называют знаком радикала. Поэтому можно часть слышать как «корень», так и «радикал», что означает один и тот же объект.

Число под знаком арифметического квадратного корня называют подкоренным числом, а выражение под знаком корня – подкоренным выражением, при этом термин «подкоренное число» часто заменяют на «подкоренное выражение». Например, в записи  число 151 – это подкоренное число, а в записи выражение a является подкоренным выражением.

При чтении слово «арифметический» часто опускается, например, запись  читают как «квадратный корень из семи целых двадцати девяти сотых».

Определение кубического корня из числа a дается аналогично определению квадратного корня. Только оно базируется на понятии куба числа, а не квадрата. Кубическим корнем из числа a называется число, куб которого равен a.

Приведем примеры кубических корней. Для этого возьмем несколько чисел, например, 7, 0, −2/3, и возведем их в куб: 7³=7·7·7=343, 0³=0·0·0=0, 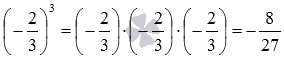. Тогда, основываясь на определении кубического корня, можно утверждать, что число 7 – это кубический корень из 343, 0 есть кубический корень из нуля, а −2/3 является кубическим корнем из −8/27.

Можно показать, что кубический корень из числа a, в отличие от квадратного корня, всегда существует, причем не только для неотрицательных a, но и для любого действительного числа a. Для этого можно использовать тот же способ, о котором мы упоминали при изучении квадратного корня.

Более того, существует только единственный кубический корень из данного числа a. Докажем последнее утверждение.

6

 Для этого отдельно рассмотрим три случая: a – положительное число, a=0 и a – отрицательное число.

Легко показать, что при положительном a кубический корень из a не может быть ни отрицательным числом, ни нулем. Действительно, пусть b является кубическим корнем из a, тогда по определению мы можем записать равенство b³=a. Понятно, что это равенство не может быть верным при отрицательных b и приb=0, так как в этих случаях b³=b·b·b будет отрицательным числом либо нулем соответственно. Итак, кубический корень из положительного числа a является положительным числом.

Теперь предположим, что помимо числа b существует еще один кубический корень из числа a, обозначим его c. Тогда c³=a. Следовательно, b³−c³=a−a=0, но b³−c³=(b−c)·(b²+b·c+c²) (это формула сокращенного умножения разность кубов), откуда (b−c)·(b²+b·c+c²)=0. Полученное равенство возможно только когда b−c=0или b²+b·c+c²=0. Из первого равенства имеем b=c, а второе равенство не имеет решений, так как левая его часть является положительным числом для любых положительных чисел b и c как сумма трех положительных слагаемых b², b·c и c². Этим доказана единственность кубического корня из положительного числа a.

При a=0 кубическим корнем из числа a является только число нуль. Действительно, если предположить, что существует число b, которое является отличным от нуля кубическим корнем из нуля, то должно выполняться равенство b³=0, которое возможно лишь при b=0.

Для отрицательных a можно привести рассуждения, аналогичные случаю для положительных a. Во-первых, показываем, что кубический корень из отрицательного числа не может быть равен ни положительному числу, ни нулю. Во-вторых, предполагаем, что существует второй кубический корень из отрицательного числа и показываем, что он обязательно будет совпадать с первым.

Итак, всегда существует кубический корень из любого данного действительного числа a, причем единственный.

Арифметическим кубическим корнем из неотрицательного числа a называется неотрицательное число, куб которого равен a. Арифметический кубический корень из неотрицательного числа a обозначается как , знак называется знаком арифметического кубического корня, число 3 в этой записи называется показателем корня. Число под знаком корня – это подкоренное число, выражение под знаком корня – это подкоренное выражение.

Хотя арифметический кубический корень определяется лишь для неотрицательных чисел a, но удобно также использовать записи, в которых под знаком арифметического кубического корня находятся отрицательные числа. Понимать их будем так: , где a – положительное число. Например, .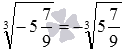

 

 

7

Свойства квадратного корня

В этом пункте мы разберемся со следующими основными свойствами арифметического квадратного корня:

1.      свойство квадратного корня из произведения двух неотрицательных действительных чисел a и b, задающееся равенством вида , его можно распространить на произведение k неотрицательных множителейa₁, a₂, …, a_k как ;

2.      корень из частного , которое часто записывают с помощью дробей как ;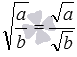

3.      свойство арифметического квадратного корня из степени числа a с четным показателем  при любом действительном a, в частности, свойство квадратного корня из квадрата числа .

В каждом из записанных равенств можно левую и правую части поменять местами, например, равенство  можно переписать как . В таком «обратном» виде свойства арифметического квадратного корня применяются приупрощении выражений столь же часто, как и в «прямом» виде.

Доказательство первых двух свойств базируется на определении арифметического квадратного корня и на свойствах степени с натуральным показателем. А для обоснования последнего свойства арифметического квадратного корня придется вспомнить определение модуля числа.

Итак, начнем с доказательства свойства арифметического квадратного корня из произведения двух неотрицательных чисел: . Для этого, согласно определению арифметического квадратного корня, достаточно показать, что  - неотрицательное число, квадрат которого равен a·b. Сделаем это. Значение выражения  неотрицательно как произведение неотрицательных чисел. Свойство степени произведения двух чисел позволяет записать равенство , а так как по определению арифметического квадратного корня  и , то .

 

8

Аналогично доказывается, что арифметический квадратный корень из произведения k неотрицательных множителей a₁, a₂, …, a_k равен произведению арифметических квадратных корней из этих множителей. Действительно, . Из этого равенства следует, что .

Приведем примеры: 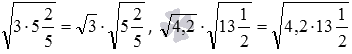 и .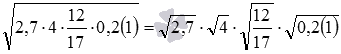

Теперь докажем свойство арифметического квадратного корня из частного: . Свойство частного в натуральной степени позволяет нам записать равенство , а , при этом  есть неотрицательное число. Это и является доказательством.

Например,  и .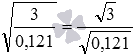

Пришло время разобрать свойство арифметического квадратного корня из квадрата числа, в виде равенства оно записывается как . Для его доказательства рассмотрим два случая: при a≥0 и при a<0.

Очевидно, что при a≥0 справедливо равенство . Также легко заметить, что при a<0 будет верно равенство . Действительно, в этом случае −a>0 и(−a)²=a². Таким образом, 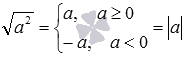, что и требовалось доказать.

Приведем примеры:  и .

Только что доказанное свойство квадратного корня позволяет обосновать следующий результат , где a – любое действительное число, а m – любое натуральное число.

9

В самом деле, свойство возведения степени в степень позволяет заменить степень a^2·m выражением (a^m)², тогда .

К примеру,  и .

Сначала перечислим основные свойства корней n-ой степени:

1.      свойство корня из произведения двух неотрицательных чисел a и b, ему отвечает равенство , это свойство распространяется на произведение k неотрицательных чисел a₁, a₂, …, a_k как ;

2.      корень из дроби обладает следующим свойством 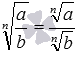, где a – любое неотрицательное действительное число, а b – положительное действительное число;

3.      при любом действительном a и четных показателях n=2·m справедливо , а при нечетных n=2·m−1 выполняется равенство .

4.      свойство корня из корня , где a – любое неотрицательное число, n иm – натуральные числа, это свойство можно распространить как ;

5.      для любого неотрицательного a и произвольных натуральных n и m справедливо равенство ;

6.      свойство корня степени n из степени неотрицательного числа a в натуральной степени m, определяемое равенством ;

7.      свойство сравнения корней с одинаковым показателем: для любых положительных чисел a и b таких, что a<b, выполняется неравенство ;

8.      свойство сравнения корней с одинаковыми подкоренными числами: если m и n такие натуральные числа, что m>n, тогда при 0<a<1 справедливо неравенство , а при a>1 выполняется .

Все записанные равенства остаются справедливыми, если в них поменять местами левую и правую части. В таком виде они употребляются также часто, в основном при упрощении и преобразовании выражений.

 

10

Доказательство всех озвученных свойств корня основывается на определении арифметического корня n-ой степени, на свойствах степени и на определении модуля числа. Докажем их в порядке очередности.

1.      Начнем с доказательства свойства корня n-ой степени из произведения . Для неотрицательных a и b значение выражения  тоже неотрицательно, как произведение неотрицательных чисел. Свойство произведения в натуральной степени позволяет записать равенство . По определению арифметического корня n-ой степени и , следовательно, . Этим доказано рассматриваемое свойство корня.

Аналогично доказывается это свойство для произведения k множителей: для неотрицательных чисел a₁, a₂, …, a_n выполняется  и .

Приведем примеры использования свойства корня n-ой степени из произведения: 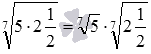 и .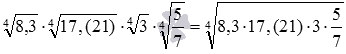

2.      Докажем свойство корня из частного 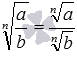. При a≥0 и b>0 выполняется условие 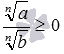, а .

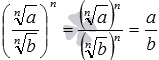Покажем примеры: 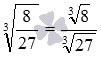 и .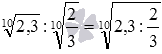

3.      Двигаемся дальше. Докажем свойство корня n-ой степени из числа в степени n. То есть, докажем, что  и  для любого действительного a и натурального m. При a≥0 имеем  и , что доказывает равенство , а равенство  очевидно. Приa<0 имеем  и 

11

 (последний переход справедлив в силу свойства степени с четным показателем), что доказывает равенство , а  справедливо в силу того, что при разговоре о корне нечетной степени мы приняли  для любого неотрицательного числа c.

Приведем примеры использования разобранного свойства корня:  и .

4.      Переходим к доказательству свойства корня из корня . Поменяем местами правую и левую части, то есть, докажем справедливость равенства , которое будет означать справедливость исходного равенства. Для неотрицательного числа a корень из корня вида  является неотрицательным числом. Вспомнив свойство возведения степени в степень, и воспользовавшись определением корня, можно записать цепочку равенств вида 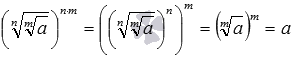. Этим доказано рассматриваемое свойство корня из корня.

Аналогично доказывается и свойство корня из корня из корня и т.д. Действительно, .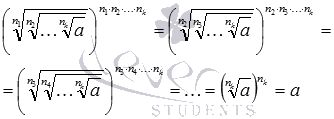

Например,  и .

5.      Докажем следующее свойство сокращения показателя корня . Для этого в силу определения корня достаточно показать, что  есть неотрицательное число, которое при возведении в степень n·m равно a^m. Сделаем это. Понятно, что если число a неотрицательное, то корень n-ой степени из числа a является неотрицательным числом. При этом , что и завершает доказательство.

Приведем пример применения разобранного свойства корня: .

12

6.      Докажем следующее свойство – свойство корня из степени вида . Очевидно, что при a≥0 степень  является неотрицательным числом. Более того, ее n-ая степень равна a^m, действительно, . Этим и доказано рассматриваемое свойство степени.

 

 

Например, .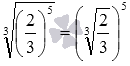

7.      Переходим дальше. Докажем, что для любых положительных чисел a и b, для которых выполняется условие a<b, выполняется неравенство . Доказательство проведем от противного. Предположим, что . Тогда по свойству степеней с натуральным показателем должно быть справедливым неравенство , то есть, a≥b. А это противоречит условию a<b. Следовательно,  при a<b.

Для примера приведем верное неравенство .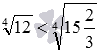

8.      Наконец, осталось доказать последнее свойство корня n-ой степени. Докажем сначала первую часть этого свойства, то есть, докажем, что при m>nи 0<a<1 справедливо неравенство . Доказательство проведем методом от противного. Предположим, что при указанных выше условиях . Свойства корня позволяют это неравенство переписать в виде . Тогда в силу свойств степени с натуральным показателем должно выполняться неравенство , то есть, a ⁿ≤ a^m. А полученное неравенство при m>n и 0<a<1 противоречит свойствам степени с натуральным показателем.

 

 

13

2. Методы извлечения квадратного корня

 

В ходе данного исследования были выявлены следующие методы извлечения квадратного корня .

1. метод оценки

2. арифметический метод

3. вавилонский метод

4. метод Ньютона

5. геометрический метод

6. метод извлечения квадратного корня столбиком

 

2.1.Метод оценки

 

Данный метод эффективно применяется при вычислении квадратных корней из чисел в диапазоне от 100 до 10 000. 

 

Алгоритм извлечения квадратного корня методом оценки

1. Ограничить искомый корень сверху и снизу числами, кратными  10, сократив диапазон поиска до 10 чисел;

2. На основании теоремы о последней цифре квадрата отобрать те, которые не могут быть корнями.

3. Возвести эти числа в квадрат. То из них, квадрат которого равен исходному числу, и будет корнем.

Рассмотрим пример извлечения квадратного корня из числа 3364.

Шаг №1 - ограничение корней. Выясним, между какими числами расположен наш корень. Желательно, чтобы эти числа были кратны десяти:

10² = 100; 20² = 400; 30² = 900; ... 90² = 8100; 100² = 10 000.

Получили ряд чисел:

100; 400; 900; 1600; 2500; 3600; 4900; 6400; 8100; 10 000.

Эти числа - границы - диапазон, в котором лежит исходный корень.

2500 < 3364 < 3600  50² < 3364 < 60²  50 <  < 60.

Шаг №2 – «отсев» лишних чисел. У нас есть 10 чисел — «кандидатов» на корень.

Последняя цифра квадрата числа равна 0, 1, 4, 5, 6 или 9, и зависит только от последней цифры исходного числа.

Другими словами, достаточно взглянуть на последнюю цифру квадрата — и  понять, на что заканчивается искомое число.

Существует всего 10 цифр, которые могут стоять на последнем месте квадрата числа. Зависимость последней цифры квадрата числа можно представить в виде следующей таблицы.

Квадратный корень из 3364 обязательно заканчивается на 2 или на 8. Получаем:

50<<60;

= *2 или = *8

 

 

14

Звездочки показывают, что мы пока не знаем этой цифры.

Но известно, что корень лежит в пределах от 50 до 60, на котором есть только два числа, оканчивающихся на 2 и 8, это числа 52 и 58

Шаг №3 - финальные вычисления. Итак, у нас осталось 2 числа-кандидата. Чтобы узнать, какое из них является корнем, необходимо возвести оба числа в квадрат. То, которое в квадрате даст исходное число, и будет корнем.

52² = (50 +2)² = 2500 + 2 · 50 · 2 + 4 = 2704;
58² = (60 − 2)² = 3600 − 2 · 60 · 2 + 4 = 3364.

Получилось, что  = 58.

 

2.2.Арифметический метод

 

Для квадратов чисел верны следующие равенства:

1 = 1²

1 + 3 = 2²

1 + 3 + 5 =3²

1 + 3 + 5 + 7 = 4² и так далее.

Узнать целую часть квадратного корня числа можно, вычитая из него все нечётные числа по порядку, пока остаток не станет меньше следующего вычитаемого числа или равен нулю. Подсчитав количество выполненных действий, определяем целую часть квадратного корня.

Недостатком такого способа является то, что если извлекаемый корень не является целым числом, то можно узнать только его целую часть.

Например: 9 − 1 = 8; 8 − 3 = 5; 5 − 5 = 0. Выполнено 3 действия, следовательно, квадратный корень числа 9 равен 3.

Аналогично найдем квадратный корень числа 12: 12 - 1 = 11; 11 - 3 = 8; 8 - 5 = 3; 3 < 7. Выполнено 3 действия, целая часть числа квадратный корень числа 12 равен 3.

 

2.3.Вавилонский метод

 

Еще 4000 лет назад вавилонские ученые составляли наряду с таблицами умножения и таблицами обратных величин (при помощи которых деление чисел сводилось к умножению) таблицы квадратов чисел и квадратных корней из чисел. Они умели находить приблизительное значение квадратного корня из любого целого числа.

Древние вавилоняне пользовались следующим методом нахождения приближенного значения квадратного корня их числа х. Число х они представляли в виде суммы а²+b, где а² ближайший к числу х точный квадрат натурального числа а, и пользовались формулой

. (1)

Извлечем с помощью формулы (1) корень квадратный, например, из числа 28:

Результат извлечения корня из 28 с помощью калькулятора 5,2915026. Как видим, метод вавилонян дает хорошее приближение к точному значению корня.

15

2.4. Метод Ньютона

 

Метод извлечения квадратного корня, известный как метод Ньютона, заключается в следующем.

Пусть а₁ — первое приближение числа  (в качестве а₁ можно брать значения квадратного корня из натурального числа — точного квадрата, не превосходящего х) .

Следующее, более точное приближение а₂ числа  найдется по формуле

.

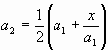Третье, еще более точное приближение

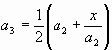и т.д.

(n+1)-е приближение  найдется по формуле

.

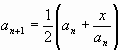Указанный способ позволяет извлекать квадратный корень из большого числа с любой точностью, правда с существенным недостатком: громоздкость вычислений.

Такой способ приближенного вычисления квадратных корней называется методом итераций.

Итерация (с латинского iteratio - повторение) - результат повторного применения какой-либо математической операции. 

Итерационная формула Ньютона для нахождения квадратного корня из числа х имеет вид:

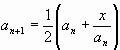
где n =2,3,4,…, а_n - n-е приближение .

Метод Ньютона приближенного вычисления квадратных корней, изложенный в одной из найденных при раскопках клинописных табличек, проиллюстрируем на следующем примере.

Найдем приближенное значение квадратного корня из 720.

Ближайшее к 720 число, из которого извлекается квадратный корень, есть число 729, оно имеет корнем 27. Разделив 720 на 27, получаем 26 . Найдем среднее арифметическое чисел 27 и 26.

(26 + 27) : 2 = 53 : 2 = .

Это и есть результат. Если возвести это число в квадрат, получим 720 .

Нахождение приближенных значений числа методом Ньютона дает следующие результаты: а₁=5; а₂= 5,3; а₃=5,2915.

 

   

 

 

16

2.5. Метод геометрических построений

 

Д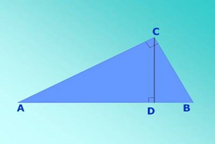анный метод извлечения квадратного корня из числа опирается на утверждение: высота в прямоугольном треугольнике, опущенная из вершины прямого угла на гипотенузу, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.

 

В частности, если , а , то .

 

Алгоритм извлечения квадратного корня геометрическим методом

 

      1. Построить в окружности (O;r) диаметр, где r = х+1;

2. На диаметре отложить отрезок ;

3. Провести СDAB, где С - точка пересечения перпендикуляра СD с окружностью (O;r);

1.     

 

 

 

 

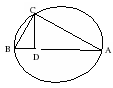
Рис. 1. Извлечение квадратного корня методом геометрических построений

Недостатком такого способа является невозможность его применения для больших чисел.

 

2.6. Извлечение квадратного корня столбиком

 

Этот способ позволяет найти приближённое значение корня из любого действительного числа с любой наперёд заданной точностью. К недостаткам способа можно отнести увеличивающуюся сложность вычисления с увеличением количества найденных цифр.

Для ручного извлечения корня применяется запись, похожая на деление столбиком. Выписывается число, корень которого ищем. Справа от него будем постепенно получать цифры искомого корня .

 

Алгоритм извлечения квадратного корня столбиком

1. Чтобы извлечь квадратный корень из данного целого числа, разбивают его справа налево на грани, по две цифры в каждой, кроме первой (крайней левой), в которой может быть и одна цифра.

2. Чтобы найти первую цифру корня, извлекают квадратный корень из первой грани.

3. Для нахождения второй цифры, из первой грани вычитают квадрат первой цифры корня, к остатку сносят вторую грань и число десятков получившегося числа делят на удвоенную первую цифру корня; полученное целое число снова подвергают испытанию.

4. Испытание проводится так: за вертикальной чертой (слева от остатка) пишут удвоенное, ранее найденное число корня, и к нему с правой стороны приписывают испытуемую цифру; получившееся после этой приписки число умножают на испытуемую цифру.

 

 

17

Если после умножения получится число, больше остатка, то испытуемая цифра не годится и надо испытать следующую меньшую цифру.

5. Следующие цифры корня находят с помощью того же приёма.Если после снесения грани число десятков получившегося числа окажется меньше делителя, т.е. меньше удвоенной найденной части корня, то в корне ставят 0, сносят следующую грань и продолжают действие дальше.

Покажем применение данного метода на примере.

П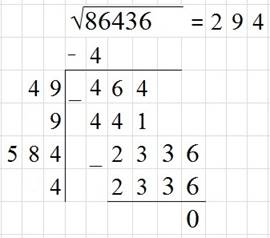ример № 1. Извлечь квадратный корень из числа 86436.

Разбиваем данное число справа налево по две цифры. У нас получилось три группы чисел (8'64'36), первое из которых однозначное число 8. Первая цифра искомого числа должна быть наибольшей, квадрат которой не превышает 8. Это цифра 2, так как 2² = 4 < 8. Квадрат её, число 4, подпишем под числом 8 и вычитаем из восьми число четыре. Сносим следующие две цифры 6 и 4. Слева от полученного числа 464 проводим вертикальную черту. Первую найденную цифру 2 удваиваем и подписываем слева от черты, оставляя место для одной цифры между четвёркой и чертой. Эту цифру подбираем так, чтобы произведение полученного двузначного числа на эту найденную цифру не превышало число 464. Этой цифрой является 9. Действительно, 49 ∙ 9 = 441 < 464. Найденная цифра 9 является второй цифрой искомого числа. Вычитаем из числа 464 число 441 и сносим последнюю пару цифр 3 и 6. Образовалось число 2336. Снова удваиваем уже число 29 и также слева от черты пишем число 58, оставляя для следующей цифры место между числом 58 и чертой. Подбираем эту цифру так, чтобы произведение этого трёхзначного числа на эту цифру было наибольшим, но не превышало числа 2336. Найденная цифра 4 является последней цифрой искомого результата, то есть квадратный корень числа 86436 будет равен 294.

Как извлечь квадратный корень.

Часто на олимпиадах и экзаменах (например, на ЕГЭ по математике) нельзя пользоваться калькулятором. Да и в быту, иногда нужно прикинуть значение квадратного корня из целого числа, не имея калькулятора под рукой. Как поступить?

1. Прежде всего, посмотрите на последнюю цифру числа, если она равна 2, 3, 7, 8, то целого корня из этого числа не существует. А если число заканчивается цифрами 1, 4, 6, 9, то последняя цифра искомого корня может быть равна, соответственно, 1 или 9, 2 или 8, 4 или 6, 3 или 7. 
Если число заканчивается цифрой 5, то нужно обратить внимание на предпоследнюю цифру. Для существования целого корня она должна быть 2-кой, т.е. только те числа, которые заканчиваются на 25, могут иметь корни с окончанием 5. 
Особое место в этом строю занимает 0. Если число заканчивается одним или нечетным числом нулей, то целого корня нет, если двумя или четным, то есть корень кратный 10-ти.

 

18

1	1 или 9	1×1 = 1	9×9 = 81
4	2 или 8	2×2 = 4	8×8 = 64
5	5	5×5 = 25
6	4 или 6	4×4 = 16	6×6 = 36
9	3 или 7	3×3 = 9	7×7 = 49
0	10	10×10 = 100

Заметили ли Вы некоторую симметрию в этой таблице? Подумайте, чем она обусловлена. Если не догадались, то посмотрите комментарий в конце этого раздела.

2. Разбейте число на группы (на грани) по 2 цифры справа налево. Начинайте с последней цифры. При этом, если заданное число состоит из нечетного числа цифр, то в крайней слева группе будет одна цифра, если из четного, то две.

Например,

Количество граней покажет количество цифр в ответе. В этих примерах из первых двух чисел могут быть извлечены трёхзначные корни, из последующих двух – двузначные.

3. Найдите примерное значение корня из первой (самой левой грани), т.е. наибольшую цифру, квадрат которой не превышает числа, стоящего в этой грани. Для примеров выше.

Если ваше число состоит только из двух граней, то на этом можно остановиться и проверить возможные результаты умножением в столбик. Например, корень из числа 1225 должен начинаться с 3 (мы это определили в п.3), а заканчиваться может только 5-кой (см. п.1), т.е. если из этого числа существует натуральный корень, то это может быть только 35. Корень из числа 841 должен начинаться с 2, а заканчиваться может 1-цей или 9-кой, т.е. это либо 21, либо 29. Но 21 ≈ 20 и 20² = 400, а 29 ≈ 30 и 30² = 900. Заданное число 841 ближе к 900, чем к 400, поэтому ответ предположительно 29.

Проверим.

  29
×29
____
261
58
____
841

    

 

 

19

35
  ×35
_____
  175
105
_____
1225

Итак, ответы существуют, они найдены и найдены верно. 
Для двузначных ответов, а более длинные числа на ЕГЭ бывают редко, всё очень просто. Не так ли?

4. Если ваше число состоит более, чем из двух граней, или вы не хотите сразу переходить к проверке, алгоритм нахождения корня продолжается следующим шагом: 
- найденную первую цифру ответа возведите в квадрат и вычтите из первой грани, к разности допишите вторую грань, получится трехзначное или четырехзначное число. Обозначим его символом A.

В наших примерах:

5. Следующая цифра должна быть наибольшей, подбираемой так:
- умножаем на 2 имеющуюся часть ответа, дописываем к ней предполагающуюся цифру и умножаем полученное число на эту же цифру. То, что получилось, вычитаем из числа А. Остаток должен быть минимально возможным положительным числом.

Например, для числа 142884 (14'28'84) найдена часть ответа - первая цифра 3 и снесена вторая грань, т.е. определено A = 528. Умножаем часть ответа на 2, получим 3×2 = 6. Теперь к 6-ке справа нужно дописать "угадываемую цифру". Определяем её примерное значение:
А = 528 ≈ 500. 500:60 ≈ 8. Поэтому подбирать начинаем с 8.
528 − 68×8 = 528 − 544 < 0. Следовательно, пробуем 7.
528 − 67×7 = 528 − 469 > 0. Следующая цифра корня 7.

Итак, в наших примерах:

20

Если у вас образовалось столько цифр, сколько граней, и при этом остаток на этом шаге равен 0, то ответ получен.

В любом случае его имеет смысл проверить умножением.

Если, цифр столько, сколько граней, но остаток не равен 0, то или была ошибка в вычислениях выше, или натурального корня из этого числа не существует. В последнем случае, если нужно всё-таки найти его значение с заданной точностью, можно добавить необходимое количество нулевых граней (00) после запятой и продолжить. 
Если граней больше, чем получено цифр, то продолжаем. В двух верхних примерах нам осталось определить только последнюю цифру, сделать это можно подбором по п.1: для числа 142884 нужно проверить умножением 372 и 378, для числа 20449 проверить 143 и 147. Но мы продолжим по общему алгоритму.

6. Образуем новое число A, добавив к остатку, полученному на предыдущем шаге следующую грань. Для получения очередной цифры ответа повторяем действия 5-го шага. Этот шаг повторяем до тех пор, пока не будет получен весь ответ.
В наших примерах:

Комментарий к извлечению целых корней

Заметили, что сумма однозначных целых чисел, квадраты которых заканчиваются на одно и то же число, равна 10? Убедимся в том, что это не случайно. Пусть эти числа x и y, тогда

x + y = 10 и y = 10 − x.

Вспомним формулу квадрата разности двух чисел

(a − b)² = a² − 2ab + b²;

и воспользуемся ею, чтобы найти квадрат y.

y² = (10 − x)² = 10² − 2·10·x + x²;

В этой сумме первое слагаемое заканчивается двумя нулями, второе нулем, значит всё выражение после сложения будет заканчиваться той же цифрой, что и x². Т.е. x² и y² заканчиваются одинаково.

 

 

 

 

 

21

Примеры вычисления корня

Вычислить √6335289_______.

Будем записывать промежуточные результаты в столбик по аналогии с делением. Черновик справа от столбика.

  6'33'52'89 | 2517.
−4
____
  233
−225    |45×5 
______
      852
    −501   |501×1 
________
      35189
    −35189   |5027×7
__________
       0

1) Разбиваем число на грани: 6'33'52'89. Получилось 4 штуки, следовательно, ответ будет состоять из 4-ёх цифр. Первая цифра 2, так как 2² = 4 < 6, a 3² = 9 > 6.

2) Далее удваиваем имеющуюся часть ответа, определяем остаток, сносим очередную грань и подбираем следующую цифру ответа. Повторяем этот шаг до последней грани:
233:40 ≈ 5; 45×5 = 225 < 233; 46×6 = 276 > 233; следовательно, 2-я цифра 5;
852:500 ≈ 1; 501×1 = 501 < 852; 502×2 = 1004 > 852; следовательно, 3-я цифра 1.

3) Если целый корень существует, то его последней цифрой может быть либо 3, либо 7. Можем проверить 2513 и 2517 умножением в столбик. Но для многозначных чисел быстрее продолжить по общему алгоритму:
35189:5000 ≈ 7; 5027×7 = 35189 (!) Последняя цифра 7.

Ответ: 2517.

Вычислить √2304____.

    48
  ×48
______
  384
192
______
2304

Разбиваем на грани. 23'04. Следовательно, ответ из 2-ух цифр, первая цифра 4, т.к.   4² = 16 < 23, a 5² = 25 > 23. Последняя цифра либо 2, либо 8, т.к. результат умножения должен заканчиваться на 4. 

22

Итак, 42 или 48? 42 ≈ 40; 40² = 1600. 48 ≈ 50; 50² = 2500. 2500 ближе к заданному числу, поэтому проверку умножением в столбик начинаем с 48.

Ответ: 48.

Это самый распространенный случай на ЕГЭ по математике, и я настоятельно рекомендую завершать его именно проверкой.

Вычислить √503___.

Число заканчивается тройкой. Сразу видно, что целого значения корня не получится. Зададимся вопросом, с какой точностью надо определить корень. Допустим, в условии сказано округлить ответ до сотых. Это означает, что получить его надо до тысячных, т.е. до 3-го знака после запятой. Поэтому к заданному числу нужно добавить еще 3 нулевые грани. И не забыть саму запятую!

  5'03,00'00'00 | 22,427.
−4
____
  103
 − 84   |42×2 
______
    1900
  −1776   |444×4 
________
      12400
     − 8964   |4482×2 
__________
        343600
      −313929   |44847×7 
____________
          29671

1) Таким образом, разбиение на грани будет таким 5'03,00'00'00. Ответ будет состоять из пяти цифр - 2 до запятой и 3 после. Первая цифра равна 2 (2² = 4 < 5, 3² = 9 > 5), последнюю цифру в данном случае мы определить не можем.

2) Далее, выполняем шаги 4,5,6 общего алгоритма, как обычно:
103:40 ≈ 2; 42×2 = 84 < 103; 43×3 = 129 > 103; следовательно, 2-я цифра 2.
1900:440 ≈ 4; 444×4 = 1776 < 1900; 445×5 =2225 > 1900; следовательно, 3-я цифра 4.
12400:4480 ≈ 3; 4483×3 = 13449 > 12400; 4482×2 = 8964 < 12400; следовательно, 4-я цифра 2.
343600:44840 ≈ 8; 44848×8 = 358784 > 343600; 44847×7 = 313929 < 343600; следовательно, 5-я цифра 7.
Мы еще не получили нулевого остатка и, может быть, не получим никогда, если искомый корень иррациональное число. Но нам это и не нужно, т.к. результат уже получен с нужной для округления точностью.

По правилам округления отбрасываем 3-ю цифру после запятой, увеличив (т.к. 7 > 5) предыдущую на единицу 22,427 ≈ 22,43.

23

Ответ: 22,43.

Вычислить √1,5____.

Чтобы вычислить корень из десятичной дроби, нужно вспомнить, что 10² = 100 и 0,1² = 0,01. Т.е. при возведении в квадрат происходит удвоение разрядов. Соответственно, для извлечении квадратного корня из десятичной дроби нам нужно, чтобы она имела четное число цифр после запятой. В этом случае мы получим целое число граней после запятой при разбиении справа налево (с конца), а значит и целое число цифр в дробной части ответа. 
Вспомним также, что к целой части числа можно дописывать сколько угодно нулей впереди, а к дробной - сколько угодно нулей в конце. Число от этого не меняется.

1 = 001; 23 = 000023; 1080 = 01080; но(!) 1080 ≠ 10800 
0,1 = 0,10; 2,3 = 2,3000; 10,80 = 0010,8000; но(!) 10,80 ≠ 100,80 и 10,80 ≠ 10,080

I способ.

1,5 = 1,50 √1,5___ = √1,50____

Допустим, что нужно дать ответ с точностью до десятых, тогда вычислять значение этого корня нужно до второго знака после запятой. Сейчас у нас 2 цифры после запятой, т.е. одна грань, поэтому добавим еще одну нулевую грань.

  1,50'00 | 1,22
−1
____
    50
  −44  |22×2
______
      600
    −484  |242×2
_______
      116

1) Рабиение на грани: 1,50'00. Результат будет из 3-ёх цифр - одна до запятой и две после. Первая цифра, очевидно, 1.

2) Далее действуем по алгоритму:
50:20 ≈ 2; 22×2 = 44 < 50; 23×3 = 69 > 50; следовательно, 2-я цифра 2.
600:240 ≈2; 242×2 = 484 < 600; 243×3 =729 > 600; следовательно, 3-я цифра 2.

3) Округляем 1,22 ≈ 1,2.

Ответ: 1,2.

 

 

24

II способ.

Умножаем и одновременно делим наше число на 10 в четной степени ( обязательно в четной, чтобы потом легко и точно извлечь корень из знаменателя). 1,5 = 1,5 × 100/100 = 150/100. Следовательно, нужно вычислить корень из 150 и разделить его на корень из 100, т.е. на 10.

Для небольших трёхзначных целых чисел просто запомнить значения корней, потому что они очень часто встречаются (см., например, в таблицах "Квадраты чисел от 1 до 25" и "Квадратные корни" здесь). Наиболее близкое к числу 150 значение квадрата целого числа 144, следовательно √150____ ≈ 12 и, соответственно, √1,5____ ≈ 12:10 = 1,2.

Ответ: 1,2.

Внимание: очень распространена ошибка, когда для определения примерного значения корня из 1,5 берут корень из 15. Запомним - четное количество нулей.

√10__ ≈ 3,16   √100___ = 10   √1000____ ≈ 31,62   √10000_____ = 100   √100000______ ≈ 316,23   √1000000_______ = 1000

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

25

Заключение

 

В ходе моего исследования, я убедился, что актуальность темы я выбрал правильную, ведь не только дети, но и взрослые не умеют вычислять квадратные корни без калькулятора, а это является важной составляющей в жизни людей. В результате проведённой работы, было найдено огромное количество способов вычисления квадратного корня, а также выявлено, что современной науке известно много таких способов, начиная со способа математиков Древнего Вавилона и заканчивая способом «Степенных рядов сложных степеней» из разделов высшей математики, но, к сожалению, не все они являются удобными и легкими в вычислениях. Методом проб и ошибок, мы пришли к выводу, что самым рациональным и точным является способ «Деление на пары через составление ребуса». В ходе исследования были проработаны все способы, а их практическое применение доказало все недостатки и преимущества каждого из методов. Была дана характеристика каждого способа по таким критериям, как точность вычислений, трудоёмкость, «требует знания формул», «для каких корней применим», «требует логики или дополнительных знаний», а также насколько способ удобен, математически красив и практичен. Каждому способу, по результатам изучения, была дана условная оценка. Самую высокую оценку получил «Деление на пары через составление ребуса» из-за удобства, точности, доступности. Самую низкую оценку мы поставили методу вещественного анализа элементарной функции: у = √х, так как он является очень долгим, при его использовании требуются дополнительные построения. В результате нашей исследовательской работы мы пришли к выводу, что извлечение квадратного корня без калькулятора является не только полезным занятием, но еще и очень увлекательным.

 

 

 

 

 

 

 

 

 

Список использованной литературы

 

1.https://zaochnik.com

2.www.berdov.com

3.nsportal.ru

4.Ru.wikipedia.org

5.Studopedia.ru

6.mathematichka.ru

 

Скачано с www.znanio.ru