Проект по математике « Из истории числа 0»

Муниципальное общеобразовательное учреждение

Средняя общеобразовательная школа № 10

 

 

 

 

Информационно- познавательный проект

по математике

« Из истории числа 0»

 

 

 

 

Выполнила:

Зайцева Екатерина Вячеславовна

МОУ «СОШ № 10» класс 5а

 

Наставник:

Казакова Надежда Сергеевна

учитель математики МОУ «СОШ № 10»

 

 

 

 

 

 

Кыштым, 2021

Содержание

 

 

Введение …………………………………………………………………………………………3

Глава 1. История возникновения цифры 0 ………………………………….............…………4

1.1  Необходимость в нуле и места его возникновения ……………..………………………...4

1.2  Появление нуля в современном значении …………………………………………………6

Глава 2. Свойства нуля и его практическое применение ………………………….………….9

2.1 Свойства нуля и его применение в разных областях знаний и жизни …………………..9

2.2 Что знают о нуле ученики …………………………………………………………………11

Заключение ……………………………………………………………………………..………14 Список литературы …………………………………………………………………………….15

Приложение 1…………………………………………………………………………………...16

 

Введение

 

Потребность в подсчёте стала очевидной для человека с самого начала формирования первобытного общества. Свои числовые системы, со специфическими цифровыми обозначениями, формировались во всех обособленных центрах цивилизации: в Египте и Древнем Вавилоне, в Китае и Индии, у южноамериканских индейцев и в античной Греции. Математика прошла путь от простейшего подсчета предметов до решения сложнейших теорем топологии. При этом история числа ноль насчитывает только мизерную часть этого срока.

Математика является одной из важнейших наук в жизни человека. Именно с ней мы встречаемся каждый день. Она развивает смекалку, интеллект, учит сравнивать, анализировать, принимать верные решения. Это одна из главных школьных наук.

Актуальность данной темы: люди в ходе изучения математики нулю не придают особого значения, ведь считают главным освоить простейшие правила совершения действий с ним. Однако, на самом деле, история числа «ноль» является одной из самых интересных загадок человечества.

Целью данного проекта является: изучение роли и значения цифры ноль в математике.

Для достижения этой цели мы должны решить следующие задачи:

- узнать, как появилась цифра 0 и что она означает;

- собрать интересные факты о ней;

- изучить свойства нуля;

- выяснить какое значение число 0 имеет в практической жизни людей;

- провести анкетирование об отношении к цифре 0 у учеников;

- сделать на основе проведенной работы выводы и заинтересовать учеников математикой.

Объект изучения – цифра 0.

Практическая значимость: возможность использования полученной информации на уроках и внеурочное время по математике, применение в повседневной жизни.

Глава 1. История возникновения цифры 0

1.1    Необходимость в нуле и места его возникновения

Происхождение, название и знак нуля имеют интересную историю. Трудно сказать, когда он появился впервые, так как многие цивилизации примерно в одно время пришли к необходимости ввести такое понятие – нуль.

Кстати, как правильно говорить «ноль» или «нуль» принципиального значения не имеет. Можно писать и так, и так. Но в математических трудах цифру ноль принято писать — «нуль» («равно нулю», «ниже нуля»), а в свободном употреблении чаще встречается «ноль».

Первое достоверное свидетельство о записи нуля относится к 876 г.; в настенной надписи из Гвалиора (Индия) имеется число 270. Некоторые исследователи предполагают, что нуль быль заимствован у греков, которые ввели в качестве нуля букву «о» в шестидесятеричную систему счисления, употребляемую ими в астрономии.

Кто первым догадался обозначить цифрой «ничего»? Мы никогда не узнаем. Можем только утверждать, что таких гениев было несколько. Кто-то придумал знак нуля в Древнем Вавилоне. Кто-то из индейцев майя – в Америке. Кто-то – в Китае. И кто-то из мудрецов Индостана обозначил пустое место тем самым кружком, которым весь мир пользуется до сих пор.

Цифра 0 дала возможность не выдумывать новых знаков для больших чисел. Теперь любое число можно было записать, используя одни и те же цифры, и уже не спутаешь 12 со 120 или 102 – если в каком-то числе есть сотни и единицы, но нет десятков, в отведенном для десятков месте достаточно написать ноль. Появилась позиционная система счисления, в которой значение цифры зависит от ее места в числе – позиции. А пользоваться ею куда удобнее…

Считают, что ноль пришёл в Индию с востока, он был изобретён на границе индийской и китайской культур. Обнаружены более ранние надписи от 683 и 686 гг. в нынешних Камбодже и Индонезии, где нуль изображён в виде точки и малого кружка.

Цифра ноль, которой мы сейчас пользуемся, пришла к нам в месте с арабскими цифрами, которые к арабским математикам попали из Индии. То есть именно в Индии изобрели десятичную позиционную систему. Но как могли раньше считать без нуля? И могли и не могли одновременно. Что-то похожее на ноль встречается еще на глиняных клинописных табличках древнего Вавилона…

Например, вавилоняне, не зная о нуле (цифре), вполне отличали числа 202 от 22. У них хоть и существовала шестидесятиричная система счисления, а не десятичная как у нас, интуитивно они понимали, что значит ноль. В пустующую ячейку записывались либо три «крючка», либо два клинышка, обозначавшие пустоту. Это делали еще около 300 года до нашей эры.

Древние греки понятия о нуле не имели. Дело в том, что греки оперировали числами в основном в прикладных целях геометрии. А длинна отрезка равная нулю не имеет практической ценности. В астрономических счислениях применялась буква «омикрон» (όμικρον). Это первая буква в слове «ouden», означающем ничто и записывающейся как О (кружочек) и означающая…. Нет, не ноль, а 70! Греки пользовались алфавитной системой записи чисел.

Римляне тоже о нуле не знали. Если записать число 388 римскими цифрами получится CCCLXXXVIII. Никакого понятия о разрядах. Как записать 0 римскими цифрами? Ответ — никак.

Как же появилась цифра 0? И в древней Греции и Египте для счета использовались камешки. Когда камешек поднимается с того места, на котором лежал при счете, от него остается ямка. Не ноль ли это? Нет, пока еще не ноль. Все что было до индийцев носило только прикладной характер и никак не может быть принято за настоящую историю изобретения ноля. Это всего лишь обозначение пустого места. А ноль — это цифра и число.

Система десятичных разрядов существовала и в Китае. Чтобы записать число 934 в столбик единиц клали 4 палочки, десятков — 3, а сотен — 9 палочек. Вместо нуля оставляли пустое место. А вот записывая цифры китайцы разряды не использовал и символа для ноля не было.

У индейцев Майа тоже был свой ноль в их двадцатеричной системе счисления, на тысячу лет раньше индийцев. Но ноль у Майа означал не ноль в нашем понимании слова, а «начало». Счет дней в календаре майя начинался с нулевого дня и назывался «Ахау».

Соседи Инки использовали узелковое письмо, где цифры от 1 до 9 обозначались разными узелками, а ноль — пустым местом.

 

 

 

1.2    Появление нуля в современном значении

 

Когда и как появился ноль в современном значении? Что же собственно изобрели индийские математики? Они записали ноль поначалу точкой, обозначая отсутствующее число, а потом и кружочком. Но главное, что они определили ноль не как понятие отсутствия числа, а как число!

Около 500 года нашей эры была разработана позиционная система записи чисел, а запись, касающаяся использования нуля, датируется 876 годом. Вот и ответ (хотя и довольно сомнительный) на вопрос «когда появился 0». Тот самый, настоящий.

Индийские математики Брахмагупта, Махавира и Бхаскара писали, что если из одного числа вычесть его же, то получится «ноль». Это и есть знакомое нам определения числа ноль. Теперь ноль — это число. Ноль используется в расчетах и даже записывается как маленький кружочек.

К какому числу его ни прибавь, оно не изменяется (ведь мы прибавили «ничего»). На какое число его не умножь, будет снова ноль (мы взяли число ноль раз, т.е. ни разу). Сам он делится на любое число (пустое место как не дели – все равно ничего не будет). Зато делить на него самого нельзя: разве можно что-то разделить на ноль частей? Если бы это удалось, как из нуля частей сложить вновь то, что мы разделили? Чтобы избежать этой неприятности, деление на ноль пришлось запретить.

Цифра 0 означает ничего, когда она стоит отдельно от других чисел. Но без него нельзя написать десятки, сотни, тысячи. Если вы уберете скромный нолик от числа 10, и оно станет в десять раз меньше. Уберите всего лишь два ничего незначащих скромных нолика от сотни, и она превратится всего лишь в единицу. А вот какую бы цифру от нуля не убирали, слева или справа – ноль всегда остается самим собой! Итак, несмотря на его ничтожное в сравнении с другими цифрами значение, только благодаря ему, создаются, как самые большие, так и самые маленькие числа. Вывод, получается, что 0 – важная цифра!

Наконец, без ноля не существовало бы современной компьютерной техники. Еще в первой половине ХIХ века немецкий инженер Конрад Цузе сконструировал первую электрическую вычислительную машину, которая оперировала цифрами "1" и "0". Ноль означал, что ток отсутствует, единица - что ток есть. Со временем на смену машине Z1 пришли ЭВМ. Но в основе их работы - все тот же принцип бинарного (двоичного) счисления.

     А представить себе современную жизнь без компьютера уже так же трудно, как и то, что когда-то наши предки испытывали ужас перед цифрой "0".

Вы, вероятно, не знаете, что ноль — это понятие изобретенное. Это одно из величайших достижений человечества, это целая теория, которая оказала влияние на историю человечества, потому что внесла большой вклад в развитие высшей математики.

До XVI века система чисел, применяемая в Европе, была римской, изобретенной около 2 тысячелетий назад. Римская система была очень непроста. Она основана на десятке. Значок «X» равен 10. Буква «С» означает 100, «М» — 1000, «I» — 1, «V» — 5, «L» — 50, «D» — 500. 4 обозначают как «IV», т.е. на один меньше, чем 5. Чтобы записать число 1648, нужно использовать следующие цифры: MDCXLVIII.

В римской системе, чтобы прочитать номер, нужно посчитать, вычитать, складывать.

Задолго до новой эры жители Индии изобрели более удобную систему счета. Она была привезена около 900 года в Европу арабскими торговцами, поэтому называется индо-арабской системой.

По индо-арабской системе все числа записывались знаками - 1, 2, 3, 4, 5, 6, 7, 8, 9 и ноль. Цифры, входящие в числа, записанные в этой системе, имели разное значение в зависимости от места, на котором они стояли.

Мы знаем, что число 10 обозначает 1 десяток, потому что единица написана на месте десятков, а ноль показывает, что место единиц — свободно, единицы отсутствуют. Число 40 означает, что десятков 4, единиц нет. Можно сказать и иначе, что в этом числе 40 единиц. Ноль показывает, что цифра 4 стоит на месте десятков.

Римляне не имели ноля в своей системе. Чтобы записать 205, они делали это так: «CCV». Они не использовали значение места, на котором стоит цифра. В индо-арабской системе мы пишем 205, помещая 2 на место сотен, ноль — на место десятков, 5 — на место единиц. 2 показывает, что сотен 2, ноль показывает отсутствие десятков, а единиц — 5.

Нужны были пути для указания значимости каждой цифры в числе. Изобретение ноля сделало это возможным. Стали употреблять слова и значки, показывающие значение места, на котором находится цифра.

С изобретением ноля в десятичной позиционной системе произошла революция – всё стало на свои места и получило строгую иерархию, а расчёты существенно упростились (наконец-то можно производить расчёты в столбик!).

Остановить прогресс было уже нельзя. Итальянский математик Леонардо Фибоначчи (1180 – 1240г.) одним из первых заинтересовался индийской системой счёта и повсеместно стал использовать цифру "0" в своих расчетах. В своем трактате "Liber Albaci" ("Книга абака"), обнародованном в 1202 году, он красочно описал преимущества этой системы счисления, прибегнув к ряду конкретных примеров из жизни купца.

В последующие века значение ноля стремительно возрастает. Ноль начинает занимать почетное место на различных числовых шкалах - например, на градусной. И ныне мы постоянно оперируем относительными показателями, то есть взятыми относительно некой условной - нулевой - отметки.    

И даже в 16 веке математики продолжали всячески избегать ноль, упёрто придерживаясь античной системы и полагаясь на счётные доски. К примеру, итальянский математик Джеронимо Кардан (1501–1576) решал кубические и квадратные уравнения без ноля. Долгое время нуль не признавали числом, лишь в концу 17 века с введением метода координат нуль начинает выступать наравне с остальными числами.

В России ноль вводился в практику стараниями Леонтия Магницкого, автора знаменитого учебника «Арифметика, сиречь наука числительная» (1703).

 

 

 

 

 

 

 

 

 

 

 

 

 

Глава 2. Свойства нуля и его практическое применение

2.1 Свойства нуля и его применение в разных областях знаний и жизни

Ноль, который разграничивает положительные и отрицательные числа, обладает уникальными математическими свойствами. Это четное, не имеющее знака натуральное целое число. Сложение с нулем и вычитание нуля никак не влияет на число, а умножение на 0 даёт ноль. Деление на ноль считается не имеющей смысла операцией, которое в случае выполнения в компьютерной программе может нанести системе существенный вред. Именно в попытке деления на 0 оказался смысл сбоя в компьютерной системе крейсера ВМФ США "Йорктаун", который произошел осенью 1997 года и привел к несанкционированному выключению двигательной установки. Некорректное отношение к числу, означающему "ничто", превратило мощный военный корабль в беспомощную неподвижную цель.

Повторим свойства нуля:

Сложение а+0=а

Вычитание а-0=а а-а=0

Умножение а*0=0

Деление 0:а=0

На 0 делить нельзя

 Значение этого числа существенно возрастало с развитием науки. Нуль возникает в областях не только чисто математических. Ноль возникает во многих разделах физики:

При измерении громкости звука в фонах за 0 принимается порог слышимости.

Минимально возможный уровень энергии квантовомеханической системы называется нулевой энергией.

Известен абсолютный нуль температуры — 0 на шкале Кельвина. В быту, однако, чаще используются другие шкалы температуры.

В частности, на шкале Цельсия за 0 произвольно принята точка замерзания воды.

В картографии известны нулевой километр, нулевой меридиан (в настоящее время — Гринвичский меридиан) и многое другое.

Нулевого года в юлианском и григорианском календарях нет, точно так же, как ни год, ни месяц не содержат нулевого дня. Однако имеется астрономическая шкала, на которой нулевой год имеется. Какое число стоит в начале шкалы многих измерительных приборов, известно и школьнику - это 0. Бинарное счисление, послужившее основой для создания современных вычислительных устройств, является позиционной системой счисления с основанием два. Это означает, что все данные, вводимые в компьютерные системы, кодируются сочетанием двух символов – единицы и нуля.

Немногим известно, что нулю был поставлен памятник в Венгрии. На сегодняшний день он является единственным числом, удостоившимся такой чести. А вот жители Москвы имеют возможность загадывать желание на нулевом километре, обозначающим начало всех дорог в стране.

Нулевой километр (англ. Kilometre Zero (km 0)) — во многих странах мира особый знак в центре столицы, символизирующий начальную точку отсчёта дорожных расстояний. Похожие знаки существуют и в других городах вне столиц — для дорог, не проходящих через столицу. Во многих городах «нулевой километр» отмечается табличкой или изображённым на земле знаком, а иногда статуей или стелой, даже исторической достопримечательностью: дворцом, башней, мостом, может и просто жилым домом. В силу исторических причин нулевой километр часто попадает на главный почтамт города. Во многих странах «нулевой километр» называют «нулевой точкой».

На любом калькуляторе после его включения сразу появляется ЕДИНСТВЕННОЕ число – цифра 0.

В полночь на электронных часах появляются четыре НУЛЯ. Начинается новый день!

КРЕСТИКИ-НОЛИКИ – логическая игра, в которой один из игроков играет “крестиками”, а второй — “ноликами”.

Жест рукой, изображающий цифру 0, в англоговорящих странах имеет значение “ВСЕ В ПОРЯДКЕ”, “ВСЕ НОРМАЛЬНО”, “ВСЕ ОТЛИЧНО”.

У русского народа, как у любого другого существует множество пословиц и поговорок. Вспомним те, в которых упоминаются числа.

Ноль без палочки (прост.).  –  Ничего не стоящий, не значащий человек.

Ноль внимания (прост.). –  Полное равнодушие, безразличие со стороны кого-либо к кому-либо или чему-либо.

Абсолютный нуль, круглый ноль. –  Человек ничтожный, совершенно бесполезный в каком-либо деле.

Сводить к нулю, свести к нулю. –  Лишать всякого смысла, значения. (сравнение –  . "сводить на нет").

Ничего не возникает из ничего. –  Это выражение принадлежит греческому философу Мелиссу, часто цитировалось древними философами, писателями.

Ничего не ново под луной. –  Это выражение, ставшее крылатым, взято из стихотворения русского писателя Н.М. Карамзина (навеяно библейским писанием).

 

2.2 Что знают о нуле ученики

Следующая часть проекта – опрос учеников о цифре 0. Была разработана анкета – опрос:

1.  Знаете ли вы цифру 0:   а) да   б) нет

2.  Как правильно говорить «нуль» или «ноль»?   _____________________________

3.  В каком веке появился, привычный нам, символ нуля «0»?   _________________

4.  Как записать 0 римскими цифрами?   ____________________________________

5.  Знаете ли вы, что есть памятник нулю?   а) да   б) нет

6.  Какое получится число, если справа от цифры 1 написать цифру 0?   _________

7.  Кем был придуман ноль?   _____________________________________________

8.  Какое число получим? а) 5+0=____   б) 5-0=____  в) 5х0=____  г) 5:0=_____

9.  В каких областях знаний «ноль» используется кроме математики?  ___________

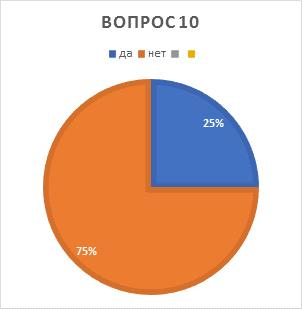
10.         Возможно ли не использовать «ноль» в современной жизни?      а) да   б) нет

11.         Как изображали ноль в древности разные народы?  _____________________

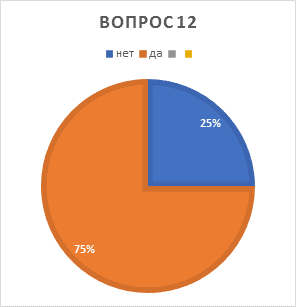
12.         Для вас цифра 0 важная или нет?   ____________________________________

Ответы на вопросы отражены в таблице. В опросе принимало участие 28 учеников.

Вопросы	Ответы учеников	Правильные ответы
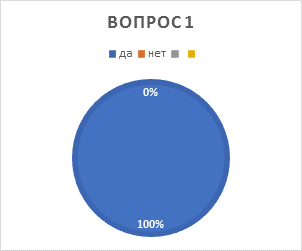
1.Знаете ли вы цифру 0:   а) да   б) нет	Да – 28чел.
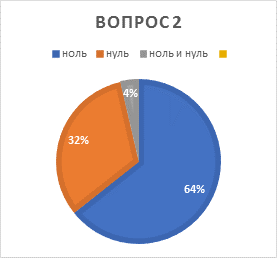
2.Как правильно говорить «нуль» или «ноль»?	Нуль – 18чел. Ноль – 9чел. И нуль и ноль – 1чел.	Можно говорить ноль и нуль.
3.В каком веке появился, привычный нам, символ нуля «0»?	Не знаю – 28чел.	IX век
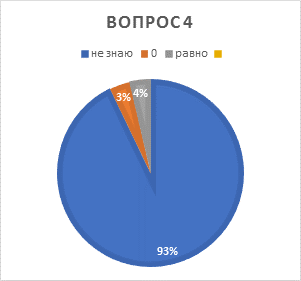
4.Как записать 0 римскими цифрами?	Не знаю – 26чел. 0 – 1чел.         ꞊ - 1чел.	Никак
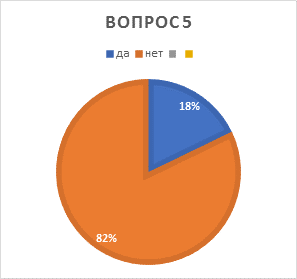
5.Знаете ли вы, что есть памятник нулю?    а) да   б) нет	Да – 5чел. Нет – 23чел.	Есть памятник нулю в Венгрии
6.Какое получится число, если справа от цифры 1 написать цифру 0?	10 – 28чел.	10
7.Кем был придуман ноль?	Не знаю – 28чел.	Многие мудрецы не зависимо друг от друга в разных государствах и континентах
8.Какое число получим?  а) 5+0=  б) 5-0=   в) 5х0=  г) 5:0=	а) 5 – 28чел. б) 5 – 28чел. в) 5 – 9чел., 0 – 19чел. г) 0 – 9чел., на 0 делить нельзя – 19чел.	а) 5 б) 5 в) 0 г) на 0 делить нельзя
9.В каких областях знаний «ноль» используется кроме математики?	Не знаю – 23чел. Алгебра – 2чел. История – 2чел. Геометрия – 1чел.	Информатика, физика, география, история, астрономия и т.д.
10.Возможно ли не использовать «ноль» в современной жизни? а) да  б) нет	Да – 7чел. Нет – 21чел.	Нет
11.Как изображали ноль в древности разные народы?	Не знаю – 28чел.	По – разному: в виде точки и малого кружка, трех «крючков», двух клинышек, ямки, пустого места
12.Для вас цифра 0 важная или нет?	Нет – 7чел. Да – 21чел.	Да

 

Анкетирование показало следующее:

·         цифру 0 знают все ученики и большинство считают её важной;

·         все правильно называют цифру 0, но не знают, что есть два варианта;

·         никто не знает историю нуля: в каком веке появился, привычный нам, символ нуля «0»; кем был придуман ноль;, как изображали ноль в древности;

·         все правильно складывают и вычитают цифру 0, но умножение и деление некоторых учеников заставляет ошибаться;

·         никто не знает, что нет обозначения нуля римскими цифрами;

·         совсем немного учеников знают, что есть памятник нулю;

·         все понимают, что без цифры 0 не получится цифры 10;

·          большинство учеников не знают, где ноль используется кроме математики, либо думают, что его применение ограничено;

·         большая часть учеников понимают, что в современной жизни невозможно не использовать ноль.

На основе проведенного опроса стало понятно, что цифру 0 знают все ученики и большинство считают её важной, а также понимают, что в современной жизни невозможно не использовать ноль. В основном ученики знают свойства нуля, но т.к. редко сталкиваются с такими примерами, некоторые начинают ошибаться в умножении и делении с нулем. Никто не знает историю нуля: в каком веке появился, привычный нам, символ нуля «0»; кем был придуман ноль;, как изображали ноль в древности. Хотя история нуля очень интересна и занимательна. Никто из учеников не знает, что нет обозначения нуля римскими цифрами, а также только один ученик смог ответить, что цифру 0 можно называть и ноль и нуль – это очень интересные факты, которые мало кто знает. Большинство учеников не знают, где ноль используется кроме математики, либо думают, что его применение ограничено, а это далеко не так. Совсем немного учеников знают, что есть памятник нулю и то скорее всего только догадываются, т.к. понимают важность цифры 0. Работа над проектом дала возможность узнать много интересных фактов о цифре 0 и понять, что цифры интересны не только с точки зрения математики, но и своей историей возникновения и применения в прошлом и настоящем.

 

 

 

 

 

 

Заключение

В ходе написания проекта сформировался вывод, что цифра 0 – это важная цифра. Без нее нельзя написать в нынешнем виде десятки, сотни, тысячи. Наши современные цифры пришли к нам из Индии через арабские страны, поэтому их и называют арабскими. Всего десятью цифрами можно записать любое даже самое большое число. Это была революция в математике. Без цифры ноль нельзя записать как самые большие, так и самые маленькие цифры. С цифрой 0 связаны важные правила в математике. Есть даже памятник цифре 0 и в каждой стране есть нулевой километр. Цель данного проекта - изучение роли и значения цифры ноль в математике достигнута. Опрос, проведенный среди одноклассников показал, что с цифрой 0 они знакомы, но не глубоко понимают ее роль и значение в математике и не знают историю её происхождения.  Было очень интересно работать над этой темой. В процессе работы можно было узнать много интересных и занимательных фактов, ранее не известных, о которых многие люди даже не догадываются. Работа над проектом помогла узнать историю возникновения числа ноль, где можно применить число 0 в других областях знаний, кроме математики, какое значение число 0 имеет в практической жизни людей, узнать, как появилась цифра 0 и что она означает, собрать интересные факты о ней, изучить свойства нуля, провести анкетирование об отношении к цифре 0 учеников, сделать на основе проведенной работы выводы. Теперь на основе этого проекта можно рассказать историю появления нуля одноклассникам, показать значимость открытия этой цифры. Следовательно задачи, которые необходимо было решить в ходе работы над проектом выполнены.

Проект помог сделать следующие выводы: ноль – это понятие изобретённое. С его появлением в десятичной позиционной системе всё стало на свои места и получило строгий порядок. Ноль – это универсальная точка отсчета. Он имеет большое значение для человечества. Мир чисел очень интересен и загадочен.

 

 

 

 

 

 

 

Список литературы

 

1.      Кессельман В.С. Удивительная история математики. - М.: ЭНАС-КНИГА, 2013

2.      За страницами учебника математики./ И.Я. Депман, Н.Я. Виленкин/ М.: Просвещение 1989 г.

3.      Математика в школе : науч.-метод. журн ­– 1989. – №4.

4.      Энциклопедический словарь юного математика. – М.: Педагогика, 1989

5.      Депман И.Я. «История арифметики» - М.: Гос. Уч.-пед.изд. Министерства просвещения РСФСР

6.      Интернет ресурсы

http://mindhobby.com/proisxozhdenie-chisla-0/

https://ru.wikipedia.org

https://interesnye-istorii.in.ua/zerohistory/

https://fb.ru/article/223393/istoriya-chisla-nol-kakim-chislom-yavlyaetsya

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Приложение 1

 

 

Скачано с www.znanio.ru