Проект "Способы умножения"

   МУНИЦИПАЛЬНОЕ АВТОНОМНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

 

 

 

ТВОРЧЕСКАЯ РАБОТА

«НЕОБЫЧНЫЕ СПОСОБЫ УМНОЖЕНИЯ»

 

 

 

 

 

                                                                                                                                  Выполнил:

обучающийся 4 «Г» класса

Калугин Ростислав

Руководитель:

Хорешко  М. И.

 

 

 

 

 

 

 

2015г.

Оглавление

1. Вступление…………………………………………………………………3

 2. Необычные способы умножения…………………………………….4

2.1. Умножение на 9 (на пальцах)……………………………………4

          2.2 .  Умножение на 11………………………………………………….5

2.3. Решетчатое умножение………………………………………...6

2.4.   Новый способ умножения по таблице Оконешникова……7

2.5. Китайский способ умножения…………………………………8-9

2.6 Умножение двузначных чисел от 10 до 20 …………………...9

2.7. Умножение двузначных чисел, у которых десятки одинаковы, а сумма единиц равна 10………………………………………………10

3. Заключение………………………………………………………………. 10

Литература…………………………………………………………………... 11

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1.    Вступление

 В школе мы изучаем способ умножения в «столбик» с помощью таблицы умножения. Это прекрасный способ известен каждому. Но у этого способа есть ряд недостатков. Нужно быть внимательным при умножении больших чисел на большие числа. И что делать, если мы вдруг забудем таблицу умножения и под рукой не окажется «шпаргалки».

Мне стало интересно, а есть ли еще какие-нибудь способы вычислений. Ведь способность быстро производить  вычисления вызывает откровенное удивление.

 

Цель работы:

         Показать необычные  способы умножения.

     

Задачи:

 

Ø    Найти как можно больше  необычных способов вычислений

Ø    Научиться их применять

Ø    Выбрать для себя самые интересные

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2. Необычные способы умножения

2.1. Умножение на 9 (на пальцах)

                      Умножение для числа 9 - 9·1, 9·2 ... 9·10 - легче выветривается из памяти и труднее пересчитывается вручную методом сложения, однако именно для числа 9 умножение легко воспроизводится "на пальцах". Нужно растопырить пальцы на обеих руках и повернуть руки ладонями от себя. Мысленно присвойте пальцам последовательно числа от 1 до 10, начиная с мизинца левой руки и заканчивая мизинцем правой руки (это изображено на рисунке).

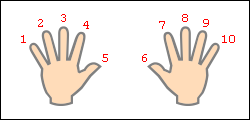
Допустим, хотим умножить 9 на 6. Загибаем палец с номером, равным числу, на которое мы будем умножать девятку. В нашем примере нужно загнуть палец с номером 6. Количество пальцев слева от загнутого пальца показывает нам количество десятков в ответе, количество пальцев справа - количество единиц. Слева у нас 5 пальцев не загнуто, справа - 4 пальца. Таким образом, 9·6=54. Ниже на рисунке детально показан весь принцип "вычисления".

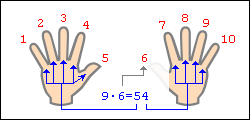
Еще пример: нужно вычислить 9·8=?. По ходу дела скажем, что в качестве "счетной машинки" не обязательно могут выступать пальцы рук. Возьмите, к примеру, 10 клеточек в тетради. Зачеркиваем 8-ю клеточку. Слева осталось 7 клеточек, справа - 2 клеточки. Значит 9·8=72. Все очень просто.

                                                                       

                                                           7                                                                                             2

 

2.2 .  Умножение на 11

Для того, чтобы умножать на 11 существует специальный метод, позволяющий совершать операции даже с большими множителями. Для начала продемонстрирую пример того, как можно умножить на 11 любое двузначное число.

Пример 42*11 решается просто.

42*11= 4 (4+2)2=462

Пишем цифры «4» и «2», а между ними «4+2». Получается 462 – это и есть верный ответ. Если сумма в скобках больше 10, тогда пишем по центру количество единиц от суммы, а к первой цифре добавляем «1».

Например:

93*11 = 9 (9+3) 3 = 1023

Конечно, можно умножить 93 на 10, и к 930 прибавить 93. Но этот несколько сложнее. В примерах с двузначными числами разницы в скорости решения между описанным выше и традиционным методами практически нет. Но если на 11 умножать большие числа, то сокращенный метод может быть более эффективным.

По сути техника умножения на 11 любого числа сводится к сложению соседних чисел. К примеру, умножим 51726 на 11. Вначале пишем первую цифру «5», затем последнюю «6», а между ними суммируем все цифры последовательно. Для верности можно проверить порядок, десятки тысяч становятся сотнями тысяч – верно.

51 726 * 11 = 5 (5+1) (1+7)(7+2)(2+6) 6 = 568 986

Если сумма в скобках дает результат больше 9, то поступаем так же как и в примере с двузначными числами. Несмотря на то, что ответ получается громоздким, мы его получили достаточно просто.

 

 

 

 

 

2.3. Решетчатое умножение

 

Сначала рисуется прямоугольник, разделённый на квадраты, причём размеры сторон прямоугольника соответствуют числу десятичных знаков у множимого и множителя. Затем квадратные клетки, делятся по диагонали.

 

Умножим этим способом 347 на 29. Начертим таблицу, запишем над ней число 347, а справа число 29.

В каждую строчку запишем произведение цифр, стоящих над этой клеткой и справа от нее, при этом цифру десятков произведения напишем над косой чертой, а цифру единиц – под ней. Теперь складываем числа в каждой косой полосе, выполняя эту операцию, справа налево. Если сумма окажется меньше 10, то ее пишем под нижней цифрой полосы. Если же она окажется больше, чем 10, то пишем только цифру единиц суммы, а цифру десятков прибавляем к следующей сумме. В результате получаем искомое  произведение 10063.

 

	3	4	7
	0	0	1
1	6	8	4	2
	2	3	6
0       2	7	6	3	9
	1
	0	6	3

 

347*29 = 10063

 

 

 

 

 

2.4.   Новый способ умножения по таблице Оконешникова

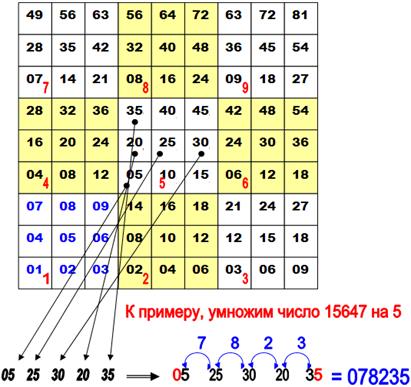
Интересен  новый способ умножения, о котором недавно появились сообщения.  Изобретатель новой системы устного счёта Василий Оконешников  составил таблицу, где все данные просто располагают в девяти ячейках, расположенных, как кнопочки на калькуляторе.

Считать по такой таблице очень просто. К примеру, умножим число 15647 на 5. В части таблицы, соответствующей пятёрке, выбираем числа, соответствующие цифрам числа по порядку: единице, пятёрке, шестёрке, четвёрке и семёрке. Получаем: 05 25 30 20 35

Левую цифру (в нашем примере - ноль) оставляем без изменений, а следующие цифры складываем попарно: пятёрку с двойкой, пятёрку с тройкой, ноль с двойкой, ноль с тройкой. Последняя цифра также без изменений.

В итоге получаем: 078235. Число 78235 и есть результат умножения.

Если же при сложении двух цифр получается число, превосходящее девять, то его первая цифра прибавляется к предыдущей цифре результата, а вторая пишется на «своё» место.

 

 

 

 

2.5. Китайский способ умножения

 

Этот способ умножения еще называют графическим. Он интересен тем, что им можно умножать достаточно большие числа, совсем не зная таблицы умножения.

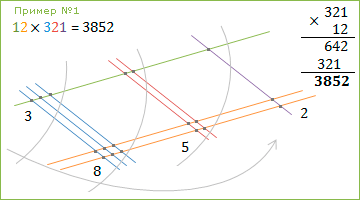
Пример №1: 12 × 321 = 3852
Рисуем первое число сверху вниз, слева на право: одна зелёненькая палочка (1),              две оранжевых палочки (2).

Рисуем второе число снизу вверх, слева на право: три голубеньких палочки (3); две красненькие (2); одну сиреневую (1).

Теперь простым карандашиком по рисунку прогуляемся, точечки пересечения чисел-палочек на части разделим и приступим к подсчёту точечек. Двигаемся справа налево (по часовой стрелке): 2, 5, 8, 3. Число-результат будем «собирать» слева направо (против часовой стрелки) и ……получили 3852 :-)

 

 

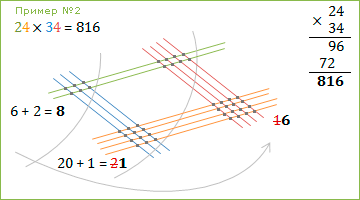
Пример №2: 24 × 34 = 816
В этом примере есть нюансы ;-) При подсчёте точечек в первой части получилось 16. Единичку отправляем-прибавляем к точечкам второй части (20 + 1)…

 

 

 

 

 

 

 

Пример №3: 215 × 741 = 159315

 

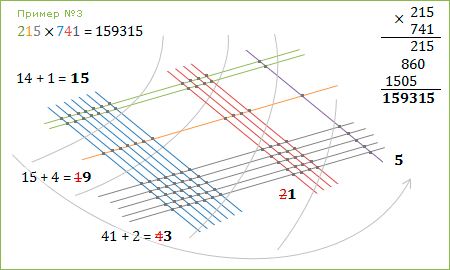
На первых порах рисовательный способ умножения показался мне сложным. А потом очень понравился своей быстротой и простотой для простых чисел.

 

2.6 Умножение двузначных чисел от 10 до 20

При перемножении двузначных чисел, лежащих между 10 и 20, нужно к одному числу прибавить единицы другого, затем к полученному приписать ноль и прибавить к этому произведение единиц обоих чисел.

Немножко сложно, но на примере совсем просто –

17*18 =306

1)    17+8 = 25

2)    25 приписываем ноль = 250

3)    7*8= 56

4)    250+56 = 306

 

Схематично это выглядит так:

      *                                                    

 

                               17   *1 8 = 250

                                                               +                  56

                                                                               306

2.7. Умножение двузначных чисел, у которых десятки одинаковы, а сумма единиц равна 10

Такие числа совсем просто умножать. Для этого нужно число десятков умножить на число, увеличенное на единицу, а затем перемножить единицы обоих сомножителей, и полученное приписать к первому произведению.

Например:

74 * 76;   7*8 = 56;   4*6 = 24. Получится 5624

52 * 58;   5*6 = 30;   2*8 = 16. Получится 3016

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 3. Заключение

Научившись считать всеми представленными способами, я пришел  к выводу, что самые простые способы это те, которые мы изучаем в школе, может быть они для нас более привычны.

Из всех найденных мною необычных способов счета более интересным показался способ «решетчатого умножения» и «китайский способ».

Заинтересовал меня новый способ умножения, потому что он  позволяет в уме «ворочать»  огромными числами.

Я думаю, что и наш способ умножения в столбик  не является совершенным и  можно придумать еще более быстрые и  более надежные способы.

                                                                                                                                                                                                                                

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Литература

1.  Интернет

2.    Перельман Я.И. Быстрый счет. Тридцать простых приемов устного счета.

3.    Перельман Я.И.  Занимательная  арифметика.

4.