Прогнозирование по регрессионной модели

Прогнозирование по регрессионной модели

Мы получили регрессионную математическую модель и мо­жем прогнозировать процесс путем вычислений. Теперь можно оценить уровень заболеваемости астмой не только для тех значе­ний концентрации угарного газа, которые были получены путем измерений, но и для других значений. Это очень важно с практи­ческой точки зрения. Например, если в городе планируется по­строить завод, который будет выбрасывать в атмосферу угарный газ, то, рассчитав его возможную концентрацию, можно предсказать, как это отразится на заболеваемости астмой жителей города.

Существует два способа прогнозирования по регрессионной модели. Если прогноз производится в пределах эксперименталь­ных значений независимой переменной (в нашем случае это кон­центрация угарного газа С), то это называется восстановлением значения.

Прогнозирование за пределами экспериментальных данных называется экстраполяцией.

Имея регрессионную модель, легко прогнозировать, производя расчеты с помощью электронных таблиц. Выберем для нашего примера в качестве наиболее подходящей квадратичную зависи­мость. Построим следующую электронную таблицу:

Подставляя в ячейку А2 значение концентрации угарного газа, в ячейке В2 будем получать прогноз заболеваемости. Вот пример восстановления значения:

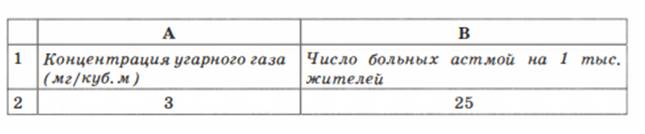
Заметим, что число, получаемое по формуле в ячейке В2, на самом деле является дробным. Однако не имеет смысла считать число людей, даже среднее, в дробных величинах. Дробная часть удалена - в формате вывода числа указано 0 цифр после запятой.

Экстраполяционный прогноз выполняется аналогично.

Табличный процессор дает возможность производить экстра­поляцию графическим способом, продолжая тренд за пределы экспериментальных данных. Как это выглядит при использова­нии квадратичного тренда для

С= 7, показано на рис . 3.6.

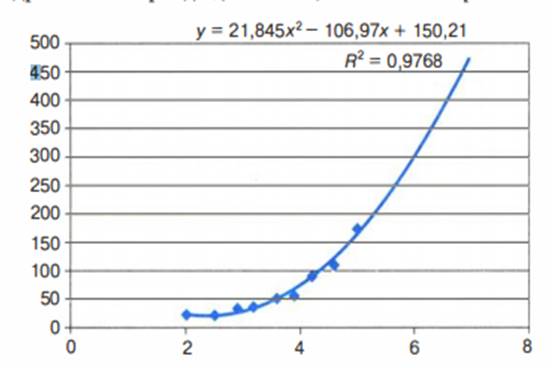
Рис. 3.6. Квадратичный тренд с экстраполяцией

В ряде случаев с экстраполяцией надо быть осторожным. Применимость всякой регрессионной модели ограничена, особенно за пределами экспериментальной области. В нашем примере при экс­траполяции не следует далеко уходить от величины 5 мг/м³. Впол­не возможно, что далее характер зависимости существенно меняет­ся. Слишком сложной является система « экология - здоровье че­ловека», в ней много различных факторов, которые связаны друг с другом. Полученная регрессионная функция является всего лишь моделью, экспериментально подтвержденной в диапазоне концентраций от 2 до 5 мг/м³ . Что будет вдали от этой области, мы не знаем. Всякая экстраполяция держится на гипотезе: «предполо­жим, что за пределами экспериментальной области закономерность сохраняется». А если не сохраняется?

Квадратичная модель в данном примере в области малых зна­чений концентрации, близких к 0, вообще не годится. Экстрапо­лируя ее на             С= 0 мг/м³, получим 150 человек больных, т. е. боль­ше, чем при 4 мг /м³. Очевидно, это нелепость. В области малых значений С лучше работает экспоненциальная модель. Кстати, это довольно типичная ситуация: разным областям данных могут лучше соответствовать разные модели.

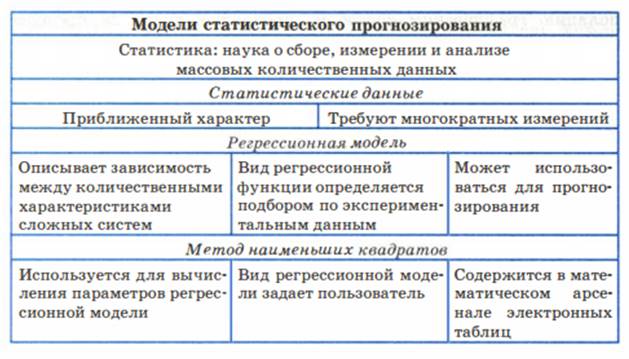      Система основных понятий