
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ УЧРЕЖДЕНИЕ
«Школа №82»
Г. О. ТОЛЬЯТТИ САМАРСКОЙ ОБЛАСТИ
ПРОГРАММА ЭЛЕКТИВНОГО КУРСА
«Учимся решать задачи»
Тольятти, 2021
Пояснительная записка
Данный курс рассчитан для учащихся 9-11 классов на 17 часов в год и предполагает изучение таких вопросов, которые входят в школьный курс в достаточно полном объеме, но сложны в усвоении. Включенный в курс материал может применяться для разных групп школьников за счет обобщенности знаниевого компонента и его преемственности с, практической направленности.
Вид курса: базовый и расширяющий уровень.
Для уверенного решения задач, в которых встречаются проценты, необходим практикум, на котором отрабатывались бы решение достаточного количества соответствующих задач. Задачи «на движение» и «на работу» так же требуют к себе достаточного внимания, т. к. они включены в экзаменационные тесты.
В целом курс выстраивается как система актуального диалога, что обеспечивается активным использованием современных методов и современных коммуникативных технологий.
В основу организации учебного процесса положена система лекционно – практических занятий. Учебный процесс организован в урочной форме: объяснение нового материала, практикумы, контрольные работы.
Изучение курса предполагается построить в виде лекций, семинаров, практикумов, уроков - сообщений, консультаций, зачетных уроков.
На всех видах занятий следует вести активный диалог с учащимися.
Разработанный дидактический материал дает возможность отбирать дополнительные задания для учащихся разной степени подготовки: уровень сложности задач варьируется от элементарных до повышенной сложности. Все задания направлены на развитие интереса и положительной мотивации изучения предмета.
Курс характеризуется рациональным сочетанием логической строгости и графической наглядностью.
Итоговое занятие предусматривает контрольную работу.
Цель учебного курса: способствовать формированию у старшеклассников математической (прагматической), социально-личностной, общекультурной и предметно-мировоззренческой компетентностей.
Математическая (прагматическая) компетентность будет способствовать:
1.Формированию интеллектуальных умений, умений и навыков самостоятельной математической деятельности, определенных государственными стандартами программы курса.
2.Обеспечению прочной математической подготовки для сдачи ЕГЭ.
Социально-личностная компетентность будет способствовать:
1.Владению стилем мышления, его абстрактностью, доказательностью, строгостью.
2.Умению ясно и точно выражать свои мысли в устной и письменной речи, выбирать из информационного потока нужный материал.
Общекультурной и предметно-мировоззренческой компетентности будет способствовать:
1. Умению понимать и объяснять значимость математики как общечеловеческой культуры.
2.Умению использовать математическую символику, термины и формулы.
3.Умению понимать особенности применения математических методов к исследованию.
Главной задачей курса является: освоение учащимися навыками решения задач различными способами (арифметическим, алгебраическим и интуитивным).
Актуальность курса определяется новизной проблем, которые ставятся перед учениками. Решение задач различными способами способствует формированию и развитию гибкости мышления, творческого мышления, развитию интеллекта.
Эффективность работы обеспечивается сочетанием работы на занятиях, а также самостоятельная работа учеников.
Изучение элективного курса в старших классах направлено на достижение следующих задач:
• помочь овладеть рядом технических и интеллектуальных умений и на уровне свободного их использования;
• продолжить развитие устного и письменного математического языка;
• продолжить работу по интеллектуальному и творческому развитию учащихся, формированию уровня абстрактного и логического мышления;
• открыть перспективные возможности успешной сдачи экзаменов на разных уровнях;
• приобщить учащихся к работе со справочной литературой.
• научить использовать теоретический материал.
Планируемый знаниевый образовательный результат:
В результате изучения элективного курс учащиеся должны приобрести следующие умения и навыки:
• уметь применять различные методы, приемы и подходы к решению задач «на проценты», «на движение» и «на работу» ;
• навыки решения уравнений и систем уравнений, вычислительные навыки;
Планируемый компетентностный образовательный результат:
1. Общекультурная компетенция:
· двигать гипотезы, находить аргументы и осуществлять их критику
2. Учебно-познавательная:
· сопоставлять, выбирать рациональные приемы; классифицировать, оценивать;
· использовать основные теоретические вопросы;
· формулировать сущностные определения;
· конструировать и опознавать связи: причинно-следственные, функциональные, структурные.
· уметь освещать последовательно, соблюдая принятые нормы устной речи.
3. Коммуникативных:
· объяснять свои действия, решения, выбор;
Описание способов оценки планируемых результатов
Для проверки знаний и умений учащихся осуществляется как текущий, так и итоговый контроль. Текущий контроль уровня усвоения материала осуществляется по результатам выполнения учащимся практикума по каждому разделу курса, практическими работами учащихся. Итоговый контроль реализуется в форме заключительной контрольной работы.
Критерии оценки планируемых образовательных результатов
Оценка «зачтено» ставиться при правильном выполнении 50% заданий контрольной или практической работы.
Оценка «не зачтено» ставиться при выполнении менее 50% заданий контрольной работы.
Характеристика ресурсов:
1. Алгебра 7 класс: учебник для общебразовательных учреждений/ [Ю.H.Макарычев, Н.Г. Миндюк, К.И.Нешков, С.Б.Суворова ]; под ред.С. А.Теляковского - М, Прсвещение, 2013.
2. Математика 6 класс: учебник для общебразовательных учреждений Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, Математика 6 класс, «Мнемозина» Москва, 2014
4. Решение задач и выполнение заданий по математике с комментариями и ответами для подготовки к ЕГЭ/ В.Н. Студенецкая, З.С.Гребнева - Волгоград: Учитель,2005.
5. Подготовка к ЕГЭ по математике в 2012 году. Методические указания/ Ященко И. В., Шестаков С. А.. Трепалин А.С..Захаров П. И. – М.:МЦНМО, 2012
6. Математика. 9-й класс. Подготовка к ОГЭ-2017: учебно-методическое пособие/ под ред. Ф.Ф. Лысенко, С.Ю. Кулабухова. – Ростов-на-Дону: Легион, 2016.
7. Уроки математического творчества / Ю. М. Куликов. – М. Просвещение,2005
8. Журнал «Математика в школе» № 3, 2017, стр 58-68.
9. Сетевые ресурсы:
10. Портал информационной поддержки Единого государственного экзамена
http://ege.edu.ru
http://alexlarin.net/
http://www.fipi.ru/
Технология реализации
1. Лекции. Практикумы.
2. Обучающие самостоятельные работы.
3. Проверочные работы.
4. Тесты.
5. Итоговая контрольная работа.
Содержание программы курса:
Тема I. Понятие процента. Задачи на проценты. (6 часов)
1. Понятие процента. Нахождение процентов от числа.
Нахождение числа по его процентам. (1ч)
2. Задачи на «концентрацию», на «сплавы» и «смеси». (1ч)
3. Задачи на сложные проценты. (2)
4. Решение задач. Обучающая самостоятельная работа. (1ч)
5. Тест. (1ч)
Тема II. Задачи на движение (5 часов)
1. Основные понятия. Решение задач на движение. (1ч)
2. Движение по воде. (1ч)
3. Движение по кругу. (1ч)
4. Задачи на движение протяженных тел (1час)
5. Решение задач. Обучающая самостоятельная работа. (1ч)
6. Самостоятельная работа. (1ч)
Тема III. Задачи на работу (3 часов)
1. Основные понятия. Решение задач. (1ч )
2. Решение задач. Обучающая самостоятельная работа. (1ч)
3. Самостоятельная работа. (1ч)
Тема IV. Решение задач из тестов ГИА и ЕГЭ. (1ч )
Итоговая контрольная работа. (1ч)
Тематическое планирование учебного материала
|
№ урока |
Тема занятий |
Количество часов |
Тип занятий |
|
I |
Понятие процента. Задачи на проценты. |
6 |
|
|
1 |
Понятие процента. Задачи на проценты. Нахождение числа по его процентам |
1 |
Лекция. Практикум |
|
2 |
Задачи на «концентрацию», на «сплавы» и «смеси». |
1 |
Сообщение. Практикум
|
|
3- 4 |
Задачи на сложные проценты |
2 |
Сообщение. Практикум |
|
5 |
Решение задач. Обучающая самостоятельная работа
|
1 |
Практикум |
|
6 |
Тест « Проценты» |
1 |
|
|
II |
Задачи на движение |
5 |
|
|
7 |
Основные понятия. Решение задач на движение |
1 |
Сообщение. Практикум. |
|
8 |
Движение по воде |
1 |
Практикум. |
|
9 |
Движение по кругу |
1 |
Сообщение. Практикум. |
|
10 |
Задачи на движение протяженных тел |
1 |
Практикум |
|
11 |
Решение задач. Обучающая самостоятельная работа |
1 |
Практикум |
|
12 |
Самостоятельная работа |
1 |
|
|
III |
Задачи на работу |
3 |
|
|
12 |
Основные понятия. Решение задач |
1 |
Сообщение. Практикум |
|
13 |
Решение задач. Обучающая самостоятельная работа
|
1 |
Практикум |
|
14 |
Самостоятельная работа |
1 |
|
|
IV |
Решение задач из тестов ГИА и ЕГЭ |
2 |
Практикум |
|
17 |
Итоговая контрольная работа |
1 |
|
Тема I. Понятие процента. Задачи на проценты.
I. Понятие процента. Задачи на проценты. Нахождение числа по его процентам.
Проценты.
Количество
процентов, которое составляет положительное число x от положительного
числа y, находится по
формуле а % = ![]() Ясно, что если число x составляет а
% от числа y, то y =
Ясно, что если число x составляет а
% от числа y, то y = ![]() и x =
и x = ![]()
При решении задач
на проценты полезно пользоваться понятиями повышающего и понижающего
коэффициентов. Смысл этих понятий таков. Если положительное число y увеличить на a %, то полученное
значение будет равно ka ![]() y, где ka = 1 +
y, где ka = 1 + ![]() - повышающий коэффициент
- повышающий коэффициент
(всегда ka >1). Если
положительное число y уменьшить на b%, то полученное
значение будет равно kb![]() y, где kb = 1 -
y, где kb = 1 - ![]() – понижающий коэффициент (всегда 0
< kb < 1). Например,
если цену y товара сначала повысили на 40%
(повышающий коэффициент 1,4), а затем понизили на 20% (понижающий коэффициент
0,8) , то новая цена станет равной 0,8
– понижающий коэффициент (всегда 0
< kb < 1). Например,
если цену y товара сначала повысили на 40%
(повышающий коэффициент 1,4), а затем понизили на 20% (понижающий коэффициент
0,8) , то новая цена станет равной 0,8![]() 1,4
1,4![]() y =1,12
y =1,12![]() y (и следовательно,
первоначальная цена оказалась повышенной на 12%).
y (и следовательно,
первоначальная цена оказалась повышенной на 12%).
Текстовые задачи на проценты
Задача 1. Разделите
данное число на части в указанном отношении: 135 пропорционально числам 6;![]()
Решение:
Пусть
k – коэффициент
пропорциональности, тогда первая часть составит 6k, вторая ![]() а третья
а третья ![]() Из условия получим уравнение:
Из условия получим уравнение:
![]() =135.
=135.
Решим это уравнение:
![]()
![]()
![]()
![]()
![]()
k=16,2.
Первая часть: 6![]() 16,2 = 97,2;
16,2 = 97,2;
Вторая часть: ![]()
Третья часть: ![]()
Ответ: 97,2; 10,8: 27.
Задача 2. Вычислите 7% от 18,4.
Решение:
I способ
1) Число, от которого находим проценты, принимаем за 100%, т.е. 18,4 составляет 100%.
1% составляет 18,4:100=0,184.
2)7%
в 7 раз больше 1%, т.е. 0,184![]() 7=1,288.
7=1,288.
II способ
Найти
7% от числа – это значит найти 0,07 от данного числа 18,4. Тогда 18,4![]() 0.07=1,288.
0.07=1,288.
III способ
Данное число 18,4 берем за 100%. Неизвестные 7% от него обозначим за х и составим схему:
100% - 18,4
7% - х
Составим решим пропорцию:
![]()
![]()
х=1,288
Ответ: 1,288.
Задача
3. Найдите число, если ![]() его равны 4,75.
его равны 4,75.
Решение:
I способ
1) Если ![]() равны 4,75 , то 1% равен:
равны 4,75 , то 1% равен:
![]()
2) Зная, что 1% равен 2,85 , найдем само число, составляющее 100%.
2,85![]() 100=285.
100=285.
II способ
Зная,
что ![]() составляют 4,75 , получим:
составляют 4,75 , получим:
![]()
![]() часть числа равна 4,75. Найдем по части
число:
часть числа равна 4,75. Найдем по части
число:
![]()
III способ
Искомое число обозначим за х, оно соответствует 100%.
Составим схему:
100% - х
![]()
Откуда составим и решим пропорцию:
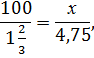
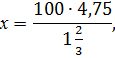
![]()
![]()
х= 285.
Ответ : 285.
Задача 4. На соревнованиях спортсмены завоевали 96 медалей, из них 35 бронзовых и 31 серебряную. Сколько процентов от общего числа медалей составили золотые медали?
Решение:
I способ
1) 96 медалей – это 100%. Тогда на 1% приходится 96:100=0,96 медали.
2) Золотых медалей 96 – 35 - 31=30. Найдем, сколько процентов составляют золотые медали от общего числа медалей:
30: 0,96=3000 : 96=31,25%
II способ
Процентное отношение обозначим за х. Составим схему:
100% - 96
X % - 30
Откуда получим и решим пропорцию:
![]()
![]()
![]()
![]()
![]()
III способ
Найдем, какую часть составляют золотые медали от общего числа медалей и умножим на 100%:
![]() =
=![]()
Ответ: 31,25%.
Задача 5. Брюки дороже рубашки на 20% и дешевле пиджака на 46. На сколько прцентов рубашка дешевле пиджака?
1 –й способ. Решение:
Рубашка – р – 100%,
Брюки - б = 1,2 р,
Пиджак
- п и б = 0,54 п, значит 1,2 р = 0,54 п, ![]() = 1,
= 1,![]() =
= ![]() ,
,
р
= ![]() п = 0,45р. Т.к. р = 1, то 1-0.45 =0.55.
п = 0,45р. Т.к. р = 1, то 1-0.45 =0.55.
2
–ой способ: Пусть брюки стоят 100 руб, тогда рубашка – 80 руб, а пиджак -146
руб. ![]()
![]() 55%.
55%.
Ответ: 55%.
Задача 6. Четыре рубашки дешевле куртки на 20%. На сколько процентов шесть рубашек дороже куртки?
Решение:
Пусть
1 куртка – 100%, тогда четыре рубашки – 80%, значит одна рубашка – 20% (80 : 4
), а шесть рубашек – 20 ![]() 6 = 120(%) и 120 – 100 = 20(%).
6 = 120(%) и 120 – 100 = 20(%).
Ответ: 20%.
Тестовые задачи на проценты


|
Ответы |
№1 |
№2 |
№3 |
№4 |
№5 |
№6 |
|
1 вариант |
4,5; 3;1,8;9 |
3 |
300 |
25 |
71,3 |
16.8 |
|
2 вариант |
120; 5; 25 |
12,6 |
130 |
10 |
120 |
70 |
2. Задачи на «концентрацию», на «сплавы» и «смеси».
При решении задач данного типа используются
следующие допущения.
1.Всегда выполняется «закон сохранения объёма или массы».
m – масса нового раствора (V – объем нового раствора)
m1 - масса первого раствора (V1 – объем первого раствора)
m2 – масса второго раствора (V2 – объем второго раствора)
m = m1 + m2 (V = V1 + V2)
2. «Закон сохранения» также выполняется для отдельных составляющих частей (компонентов) сплава(раствора)
3. Используется понятие объёмная и массовая концентрация (число, показывающее, какую долю всего объёма или массы составляет данная компонента.
Имеется 40% раствор соли, (значит в нем) 0,4 объёма занимает «чистая» соль и объёмная концентрация соли в растворе равна 0,4.
Если сплав
содержит свинец и медь в отношении 4:7, то в этом сплаве ![]() частей от массы всего сплава составляет
масса свинца,
частей от массы всего сплава составляет
масса свинца, ![]() - масса меди.
- масса меди.
Задача: Два сплава с массами m1 и m2 кг содержат медь и серебро в отношениях 12:1 и 16: 3 соответственно. Эти два сплава сплавили с m3 кг чистого серебра и m4 кг чистой меди. Определите процент серебра в образовавшемся сплаве.
1 сплав – m1
2 сплав – m2
Ag – m3
Cu – m4
Найдем массу «нового» сплава по закону сохранения : m1 + m2 + m3 + m4 .
![]() По закону сохранения массы
По закону сохранения массы
получаем массу серебра в «новом» сплаве:
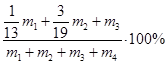 Следовательно, процентное содержание
серебра в новом сплаве
Следовательно, процентное содержание
серебра в новом сплаве
Задача 2
При смешивании 5% -го и 40% -го растворов кислоты получили 140 граммов 30% -го раствора. Сколько граммов каждого раствора нужно было для этого взять?
Решение: Возьмем по 100г каждого раствора и в соответствии с процентным
составом разделим их содержимое на кислоту и воду.
1 р-р
|
5 |
95 |
2 р-р
|
40 |
60 |
3 р-р - 140г
|
30 |
70 |
Сравним исходные составы с тем, что должно получиться после смешивания
|
5 |
|
|
|
|
30 |
|
Разница 25 частей
|
40 |
|
|
|
30 |
|
|
Разница 10 частей
140 г : ( 25 + 10 ) = 4 (г ) – приходится на 1 часть
4 ![]() 25 = 100(г) -
масса второго раствора
25 = 100(г) -
масса второго раствора
4 ![]() 10= 100(г) -
масса первого раствора
10= 100(г) -
масса первого раствора
Ответ: 40г, 100г
Алгебраический способ.
1. С помощью уравнения с одним неизвестным.
Пусть х г масса первого раствора, тогда масса второго (140 – х) г. Масса кислоты в первом растворе 0,05х г, а во втором – 0,4(140-х) г. Масса кислоты в новом растворе составляет – (0,3 · 140) г или
(0,05х + 0,4(140-х)) г. Составим и решим уравнение:
0,05х + 0,4(140-х) = 0,3 · 140
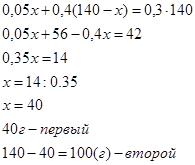
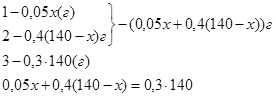 Пусть х г масса кислоты в
первом растворе.
Пусть х г масса кислоты в
первом растворе.
Ответ: 40г, 100г
Способ «креста» или схема Пирсона
( Карл Пирсон английский математик, статистик, биолог и философ )
Это удобный и рациональный способ решения задач. Метод состоит в следующем: при расчетах записываем одну над другой массовые доли растворенного вещества в исходных растворах, справа между ними – его массовую долю в растворе, который нужно приготовить, и вычитаем по диагонали из большего меньшее значение. Разности их вычитаний показывают массовые доли для первого и второго растворов, необходимые для приготовления нужного раствора.
|
|
![]() 30 – 5
= 25
30 – 5
= 25
|
|
40 – 30 = 10
|
40 |
![]() =
=![]() = 5 : 2 (в таком отношении вступают
растворы).
= 5 : 2 (в таком отношении вступают
растворы).
140 ![]()
![]() = 100(г) масса второго раствора,
= 100(г) масса второго раствора,
140 ![]()
![]() = 40(г) масса первого раствора.
= 40(г) масса первого раствора.
«Метод рыбки»
Впервые в России такой способ решения задач был описан в арифметике 18 века, автором которой был замечательный русский математик и педагог Леонтий Филиппович Магницкий. При решении задач этим способом строится схема, похожая на рыбку, вот поэтому он так и называется. Метод состоит в следующем: друг под другом записываем содержания веществ имеющихся растворов (смесей, сплавов), слева от них и примерно посередине - содержание вещества в растворе (в смеси или в сплаве), который должен получиться после смешивания. Соединяем написанные числа прямыми. В каждой паре из большего числа вычитаем меньшее, и результат записываем в конце соответствующей прямой. Получаемые массовые доли показывают, в каком отношении надо слить исходные растворы (смеси, сплавы). Записываем пропорцию и решаем её.
Решим задачу «Методом рыбки»
Для приготовления торта «Воздушный» маме требуется 10 г 40% раствора лимонной кислоты. Какова масса 20% и 70% растворов лимонной кислоты, которые она смешала, чтобы получить раствор нужной концентрации?
|
20% , х г |
|
40%, 10 г |
 30 массовых долей
30 массовых долей
20 массовых долей
|
70%, (10 – х)г |
40 – 30 = 10
Решение:
составляем пропорцию ![]() =
= ![]() и решаем её;
и решаем её; ![]() =
= ![]()
2х = 30 - 3х; 5х = 30; х = 6.
6(г) - масса 20% раствора;
1) 10 – 6 = 4(г) - масса 70% раствора
Ответ: 6 грамм 20% раствора и 4 грамма 70% раствора.
2. С помощью системы двух уравнений с двумя переменными.
Решение задачи с помощью системы уравнений обычно проводят в такой последовательности:
1. Вводят переменные, т.е. обозначают буквами х, у, z… величины, которые требуется найти по условию задачи, либо те, которые необходимы для отыскания искомых величин;
2. Используя введенные переменные, а также указанные в условии задачи конкретные значения переменных и соотношения между ними, составляют систему уравнений, т.е. «переводят» текст задачи на язык алгебры, составляя систему равенств алгебраических выражений.
3. Решают составленную систему уравнений и из полученных решений отбирают те, которые подходят по смыслу задачи.
Практикум по решению задач.
Задача 1.
Первый сплав содержит 25% цинка, второй — 40% цинка. Из этих двух сплавов получили третий сплав, содержащий 30% цинка. В каком отношении были взяты сплавы?
Ответ: 2:1.
Задача 2.
Первый сплав содержит 13% серебра, второй — 20% серебра. Из этих двух сплавов получили третий сплав, содержащий 15% серебра. В каком отношении были взяты сплавы?
Ответ 5:2.
Задача 3.
При смешивании первого раствора сахара, концентрация которого 10 %, и второго раствора сахара, концентрация которого 60 %, получили раствор, содержащий 40 % сахара. В каком отношении были взяты первый и второй растворы?
Ответ 1:2.
Задачи для самостоятельного решения:
Задачи на сплавы
1. В сплаве меди и цинка 20% меди. Масса сплава 1200г. Выясните:
а) сколько в сплаве меди;
б) сколько в сплаве цинка;
в) какой процент цинка в сплаве;
г) какой процент составляет масса меди от массы цинка;
2. К 40%-ому раствору кислоты добавили 50г чистой кислоты, после чего концентрация раствора стала равной 60%. Найдите первоначальный вес раствора.
3. Какое количество воды надо добавить в 1литр 9% -ного раствора уксуса, чтобы получить 3% -ый раствор?
4. Сплавили два слитка, содержание цинка в которых было 64% и 84% соответственно. Получили сплав, содержащий 76% цинка. Его вес 50г. Сколько весит каждый из сплавленных слитков?
5. Имеется два куска сплава меди и цинка с процентным содержанием меди 30% и 55% соответственно. В каком отношении нужно взять эти сплавы, чтобы переплавив, получить сплав, содержащий 40% меди?
6. Какое количество воды надо добавить к 2-м литрам 18% - ного раствора соли, чтобы получить 16% -ный раствор?
7. Имеется два кислотных раствора: один 20%, а другой 30%. Взяли 0,5 л первого раствора и 1,5 л второго и образовали новый раствор. Какова концентрация кислоты в новом растворе? Ответ: 27,5%
8. Имеется кусок сплава меди с оловом общей массой 20кг, содержащий 55% меди. Сколько кг чистого олова надо прибавить к этому куску сплава, чтобы получившийся новый сплав содержал 40% меди. Ответ: 7,5.
9. Имеются два слитка. Масса первого слитка в 2 раза больше массы второго. В первом слитке содержится 30% серебра, а во втором -42% серебра. Сколько процентов серебра содержится в сплаве, полученном из этих слитков? Ответ: 34%.
Тест «Проценты»
|
№ |
1 вариант |
2 вариант |
|
А1
|
В каком отношении нужно смешать 10%-й и 25%-й растворы аммиачной селитры, чтобы приготовить из них 15%-й раствор селитры? |
Первый сплав содержит 10% меди, второй — 40% меди. Из этих двух сплавов получили третий сплав, содержащий 30% меди. В каком отношении были взяты сплавы? |
|
А2
|
Смешали 500г 10%-го раствора соли и 400г 55%-го раствора соли. Определите концентрацию соли в смеси. |
В сосуд, содержащий 5 литров 12%-го водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора? |
|
А3
|
Морская вода содержит 5% соли (по массе). Сколько пресной воды нужно добавить к 30кг морской воды, чтобы концентрация соли составила 1,5%? |
Имеется 4 литра 20%-го раствора спирта. Сколько воды в него нужно добавить, чтобы получился 10%-й раствор спирта?
|
|
В1
|
Из сосуда, доверху наполненного 97%-ным раствором кислоты, отлили 2 литра жидкости и долили 2 литра 45%-ого раствора этой же кислоты. После этого в сосуде получился 81%-ый раствор кислоты. Сколько литров раствора вмещает сосуд? |
Имеется два раствора некоторого вещества. Один 15%-ный, а второй 65%-ный. Сколько нужно взять литров каждого раствора, чтобы получить 200л раствора, содержание вещества в котором равно 30%?
|
|
В2
|
Сухофрукты содержат 28% воды, а свежие – 88%. Сколько килограммов сухофруктов получится из 720 кг свежих фруктов? |
Сухофрукты содержат 24% воды, а свежие – 92%. Сколько надо взять свежих фруктов, чтобы получить 40 кг сухофруктов? |
|
С1
|
К 20%-ному раствору добавили 5 килограммов соли, и он стал 36%-ным. Сколько ещё соли нужно добавить, чтобы получить 60%-ный раствор? |
К 25%-ному раствору добавили 6 литров соли, и он стал 40%-ным. Сколько ещё соли нужно добавить, чтобы получить 50%-ный раствор? |
|
С2 |
Из кувшина, доверху наполненного 20%-ным раствором соли, отлили 1 литр и затем долили водой доверху. После этого повторили проделанные действия и получили 5%-ный раствор соли. Какова вместимость кувшина? |
Из кувшина, доверху наполненного 20%-ным раствором соли, отлили 1 литр и затем долили водой доверху. После этого повторили проделанные действия и получили 11,25%-ный раствор соли. Какова вместимость кувшина? |
Ответы:
|
№ |
1 вариант |
2 вариант |
|
А1
|
2:1 |
1:2 |
|
А2
|
30% |
5% |
|
А3
|
70 кг |
4 л |
|
В1
|
6,5 л |
140 л и 60 л |
|
В2
|
120 кг |
380 кг |
|
С1
|
15 кг |
6 л |
|
С2
|
2 л |
4 л |
3. Задачи на сложные проценты
Задачи на сложные проценты встречаются при рассмотрении схем расчетов банка с вкладчиками и заемщиками. За хранение сбережений вкладчика и разрешение распоряжаться этими деньгами банк выплачивает вкладчику проценты к хранящейся сумме денег. В зависимости от способа начисления проценты делятся на простые и сложные.
1. Простые проценты
Увеличение вклада S0 по схеме простых процентов характеризуется тем, что сумма процентов в течении всего срока хранения определяются исходя только из первоначальной суммы вклада S0 независимо от срока хранения и и количества периодов начисления процентов. Рассмотрим эту схему.
Пусть
вкладчик открыл сберегательный счёт и положил на него S0 руб. Пусть банк обязуется
выплачивать вкладчику в конце каждого года р% от первоначальной суммы S0 .Тогда по
истечению одного года сумма начисленных процентов составляет ![]() руб., и величина вклада станет равной S1 = S0
руб., и величина вклада станет равной S1 = S0![]() ( 1+
( 1+ ![]() ) руб., р% называют годовой процентной ставкой.
) руб., р% называют годовой процентной ставкой.
Если по происшествии одного года вкладчик снимает со счёта начисленные
проценты ![]() ,а сумму S0 оставит в банке,
то по происшествии второго года на вклад вновь начислят
,а сумму S0 оставит в банке,
то по происшествии второго года на вклад вновь начислят ![]() руб , а за два года начисленные
проценты составят
руб , а за два года начисленные
проценты составят ![]() руб..
руб..
Но
вкдадчик
может поступить иначе. Он может не снимать ![]() руб. начисленных в конце первого года, а всю
сумму S1 = S0
руб. начисленных в конце первого года, а всю
сумму S1 = S0![]() ( 1+
( 1+ ![]() ) руб
) руб
оставить
в банке ещё на год. Однако по происшествии второго года банк начислит р% не
на сумму S1 лежащую на счете,
а только на первоначально положенную сумму S0![]() .На величину
.На величину ![]() руб никаких начислений банк не
производит! В этом и состоит особенность начисления по схеме простых
процентов: проценты начисляются всегда только на первоначально положенную сумму
S0
руб никаких начислений банк не
производит! В этом и состоит особенность начисления по схеме простых
процентов: проценты начисляются всегда только на первоначально положенную сумму
S0![]() .
.
Теперь
понятно, что если вкладчик будет держать свои деньги на счёте n лет, то сумма Пп
начисленных процентов составит Пп = ![]() руб. , а величина первоначального
вклада вместе с начисленными процентами составит Sn = S0
руб. , а величина первоначального
вклада вместе с начисленными процентами составит Sn = S0![]() ( 1+
( 1+ ![]() ) руб. Эту формулу называют формулой
простых процентов,
или формулой простого процентного роста.
) руб. Эту формулу называют формулой
простых процентов,
или формулой простого процентного роста.
Начисление простых процентов удобно применять тогда, когда по истечении каждого года вкладчик будет снимать со своего счёта проценты, начисленные за этот год.
Отношение
![]() = 1 +
= 1 + ![]() называют коэффициентом наращения простых процентов. Он показывает,
во сколько раз вырос первоначальный вклад S0 за n лет хранения этой
суммы в банке по схеме простых процентов с годовой процентной ставкой
р% .
называют коэффициентом наращения простых процентов. Он показывает,
во сколько раз вырос первоначальный вклад S0 за n лет хранения этой
суммы в банке по схеме простых процентов с годовой процентной ставкой
р% .
Если
число ![]() выразить десятичной дробью 0,01р и обозначить её i, то формулы примут
более простой вид:
выразить десятичной дробью 0,01р и обозначить её i, то формулы примут
более простой вид:
Sn = S0![]() ( 1+ n
( 1+ n![]() i),
i), ![]() = 1 + n
= 1 + n ![]() i.
i.
2.Капитализация простых процентов
Рассмотрим ситуацию. когда банк начисляет проценты не только на первоначальную сумму, а и на начисленные за год проценты. Так называемая капитализация процентов.
Пусть вклад S0 руб находится на
счете банка t1 лет . Пусть
банк обязуется выплачивать вкдадчику в конце каждого года р1 %
годовых.По проишествии лет величина вклада станет равной S1 = S0![]() ( 1+
( 1+ ![]() ).
).
Далее вкладчик может снять эти деньги и внести их в другой (или в тот же ) банк, который в течение t2 лет будет начислять уже на сумму S1 простые проценты по ставке р2 % годовых. По проишествии (t1 + t2 ) лет величина вклада станет равной
S2 = S1![]() ( 1+
( 1+ ![]() ) = S0 ( 1+
) = S0 ( 1+ ![]() )
) ![]() ( 1+
( 1+ ![]() ) .
) .
Такая операция называется капитализация процентов. Для сложных процентов это выглядит иначе.
2. Сложные проценты
Пусть некоторая величина S0 увеличивается n раз (n лет) и каждый раз на р%. Тогда ее значение S1 для сложных процентов после первого увеличения (к концу первого года) вычисляется по формуле:
S1 =
S0 + S0 (0,01р) = S0
![]() (1 + 0,01р).
(1 + 0,01р).
В конце второго года S2 = S1 +
S1 (0,01р) = S1 ![]() (1 +
0,01р) =
(1 +
0,01р) =
S0 (1 + 0,01р)2 . т.е. идет начисление процентов на проценты.
В конце третьего года S3=
S2 + S2 (0,01р) = S2 ![]() (1
+0,01р) = S0(1
+0,01р)2
(1
+0,01р) = S0(1
+0,01р)2
![]() (1 +0,01р)=S0(1
+0,01р)3 =
S0 (1 + a)3.
(1 +0,01р)=S0(1
+0,01р)3 =
S0 (1 + a)3.
Тогда для сложных процентов сумма через n лет равна:
Sn = S0 (1 + 0,01р)n или Sn = S0 (1 + a)n , где а = 0,01 р.
Формула сложных процентов связывает четыре величины: S0 , р%,n, Sn .
1) Операция нахождения первоначальной суммы вклада называется дисконтирование
S0 =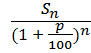 .
.
2) Нахождение n из формулы Sn = S0 (1 + 0,01р)n .
![]() =
= ![]() , прологарифмируем по основанию е.
, прологарифмируем по основанию е.
n ln(1 + 0,01р) = ln
![]() , n =
, n = 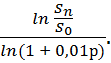
3)
Нахождение
p из формулы Sn = S0 (1 + 0,01р)n.Возведем левую и
правую часть в степень ![]() .
.
(1
+ 0,01р) = ![]() , 0,01р =
, 0,01р = ![]() - 1, p = 100(
- 1, p = 100( ![]() - 1 ).
- 1 ).
Решение задач, когда проценты начисляются не через год , а например за k месяцев (полгода, квартал и т. д.).
Пусть некоторая величина S0 увеличивается n раз (n лет) и каждый раз на р%, а k число месяцев, через которые происходит начисление процентов, тогда
![]() % за 1 месяц,
% за 1 месяц, ![]()
![]() k за k месяцев и сумма
начисленная за это время составит S0
k за k месяцев и сумма
начисленная за это время составит S0 ![]()
![]()
![]() k.. Тогда общая сумма
составит (простые проценты)
k.. Тогда общая сумма
составит (простые проценты)
Sn = S0 (1 + ![]()
![]() k), а сложные
проценты - Sn = S0 (1 +
k), а сложные
проценты - Sn = S0 (1 + ![]() ) n
) n![]() k .
k .
Накопительная сумма будет возрастать тем быстрее, чем чаще начисляют проценты.
Если на каждом этапе прирост свой ( 1 этап – р1%, 2 этап – р2%, 3 этап – р3%), то формула для вычисления Sn будет выглядеть так:
Sn = S0 (1 + 0,01р1) (1 + 0,01р2) (1 + 0,01р3).
Практикум по решению задач
Решим задачи:
1. В банке открыт срочный депозит на сумму 50 тыс. руб под 12% на три года. Рассчитать накопленную сумму если проценты а) простые ,
б) сложные.
|
а) S3 = 50 (1 +
0,12
|
б) S3 = 50 (1 + 0,12)3 = 70246 руб |
Ответ: а) 68000 , б) 70246.
2. В банке открыт срочный депозит на сумму 50 тыс. руб под 12% на три года. Рассчитать накопленную сумму, если проценты начисляются ежеквартально.
1 квартал – 3 месяца, значит 4 раза начисляют проценты.
k = 4,
n =3 , S0 =50тыс. руб ,
p= 12%. Sn = S0 (1 + ![]() )nk
)nk
S3 =
50 (1
+ ![]() ) 3
) 3![]() 4
4 ![]() 71288 руб.
71288 руб.
Ответ: 71288.
3. Торговая база закупила оборудование и поставила в магазин по оптовой цене, которая на 30% больше цены изготовителя. Магазин установил розничную цену на 20% выше оптовой. При распродаже магазин снизил цену на 10 %. На сколько рублей больше заплатил покупатель по сравнению с ценой изготовителя, если при распродаже приобрел товар за 140 руб 40 коп.
Sn = 140,40 руб, S0 = ? р1 = 30%, р2 = 20%, р3 = 10 %.
Sn = S0 (1 + 0,01р1) (1 + 0,01р2) (1 + 0,01р3),
140,4= S0 (1 + 0,3 (1 + 0,2) (1 - 0,1), S0 = 100, 140,4 – 100 =40 ,4.
Ответ: 40,4
4. В течении года предприятие дважды увеличивало выпуск продукции на одно и то же число процентов. Найдите это число, если известно, что в начале года предприятие ежемесячно выпускало 600 изделий, а в конце года стал выпускать ежемесячно 726 изделий.
Решение: Пусть S0 – начальная цена, S2 – конечная цена, р – постоянное количество процентов.
По
формуле р = 100 ![]() ((
((![]() )1/n – 1)
)1/n – 1)
получаем: р = 100 ![]() ((726 / 600 )1/2 –
1) = 10%.
((726 / 600 )1/2 –
1) = 10%.
Ответ: 10.
Задачи для самостоятельного решения
Задача 1.
Владелец автозаправки повысил цену на бензин на 10%. Заметив, что количество клиентов резко сократилось, он понизил цену на
10 %. Как после этого изменилась начальная цена на бензин? (повысилась или понизилась и на сколько % -ов?)
Ответ: понизилась на 1%.
Задача 2.
В течении года предприятие дважды увеличивало выпуск продукции на одно и то же число процентов. Найдите это число, если известно, что в начале года предприятие ежемесячно выпускало 600 изделий, а в конце года стал выпускать ежемесячно 726 изделий.
Ответ: 10.
Задача 3.
Цена на компьютерную технику были повышены на 44%. После этого в результате двух последовательных одинаковых процентных снижений цена на компьютеры оказалась на 19% меньше первоначальной. На сколько процентов каждый раз понижали цену?
Ответ: 25.
Задача 4.
Для определения оптимального режима повышения цен фирма решила с 1 января повышать цену на один и тот же товар в двух магазинах двумя способами. В одном магазине – в начале каждого месяца (начиная с февраля) на 2%, в другом – через каждые два месяца, в начале третьего (начиная с марта) на одно и то же число процентов, причем такое, чтобы через полгода (1 июля) цены снова стали одинаковыми. На сколько процентов надо повышать цену товара через каждые два месяца, во втором магазине?
Ответ: 4,04.
Тема II. Задачи на движение
Задачи на движение обычно содержат следующие величины:
t – время, в течение которого движется тело,
v – скорость движения,
S – путь , пройденный за время t .
Уравнения, связывающие эти три величины:
S = vt, t = ![]() , v =
, v = ![]() . vсреднее =
. vсреднее = ![]() .
.
Решение задачи с помощью уравнения обычно проводят в такой последовательности:
1.Вводят переменную, т.е. обозначают буквой х величину, которую требуется найти по условию задачи, либо ту, которая необходима для отыскания искомых величин.
2. Используя введенную переменную, а также указанные в условии задачи конкретные значения переменных и соотношения между ними, составляют уравнение, т.е. «переводят» текст задачи на язык алгебры, составляя равенство алгебраических выражений.
3. Решают составленное уравнение и из полученных решений отбирают те, которые подходят по смыслу задачи.
Практикум по решению задач .
Решим задачи:
Задача 1.
От двух пристаней, расстояние между которыми 250км, вышли навстречу друг другу теплоход со скоростью 50км/ч и катер со скоростью 30 км/ч. Катер вышел на 3 ч раньше, чем теплоход. Через сколько часов после выхода теплохода произойдет встреча?
Решение:
Пусть
теплоход был в пути t часов и прошел со скоростью 50км/ч расстояние 50![]() t км. Катер вышел
на 3 часа раньше и был в пути (t+3) часов со скоростью 30 км/ч, пройдя 30(t+3) км. При
встрече теплоход и катер прошли совместно 250км, откуда получим уравнение:
t км. Катер вышел
на 3 часа раньше и был в пути (t+3) часов со скоростью 30 км/ч, пройдя 30(t+3) км. При
встрече теплоход и катер прошли совместно 250км, откуда получим уравнение:
50t+30(t+3)=250,
50t+30t+90=250,
80t=160,
t=2.
2 ч - время, через которое произойдет встреча.
Ответ: 2 ч.
Задача 2.
Два поезда отправились одновременно из А и В навстречу друг другу. Скорость первого поезда на 10 км/ч больше скорости второго. Поезда встретились в 28 км от середины расстояния АВ. Если бы первый поезд отправился из А на 45 минут позже второго, то они встретились бы на середине расстояния АВ. Найдите расстояние АВ и скорости обоих поездов.
Решение:
Пусть
скорость второго поезда v км/ч, тогда скорость первого –(v+10) км/ч. Пусть
расстояние АВ=2S км, тогда первый поезд до встречи проехал (S+28) км, а второй
- (S - 28) км. Время
первого поезда ![]() ч, а второго –
ч, а второго – ![]() ч, и они равны, откуда получим уравнение:
ч, и они равны, откуда получим уравнение:
![]() . (1)
. (1)
Если
встреча произошла на середине пути, то второй поезд ехал ![]() ч, а первый
ч, а первый ![]() ч, что на 45 мин =
ч, что на 45 мин = ![]() ч быстрее времени второго, откуда получим
уравнение:
ч быстрее времени второго, откуда получим
уравнение:
![]() =
= ![]() (2)
(2)
Решим систему уравнений(1) и (2):
Так как скорость и расстояние – положительные величины, то v = 70км/ч, S=420 км, скорость первого поезда равна 70+10=80км/ч.
Ответ: 420км; 80км/ч; 70км/ч.
5. Автобус едет из пункта А в пункт В сначала 2 минуты с горы, а затем 7 минут в гору. Обратный путь он проделывает за 15 минут. Во сколько раз быстрее автобус еде с горы, чем в гору?
Решение:
Пусть скорость в гору v км/мин, а с горы в k раз быстрее, т.е. kv км/мин.
Расстояние из А в В в гору за 7 мин равно 7v км, а с горы за 2 мин – 2kv км.
На
обратной дороге пути в гору и с горы меняются. С горы 7v км автобус
проехал за ![]() =
=![]() мин, а в гору 2 kv км он проехал за
мин, а в гору 2 kv км он проехал за ![]() Итак, время на обратную дорогу составило
(2k +
Итак, время на обратную дорогу составило
(2k + ![]() мин, или по условию 15 мин.
мин, или по условию 15 мин.
2k + ![]() ,
,
2k2 + 7=15k,
k = 0.
2k2 - 15k + 7=0,
K =0.
k = 7,
k =0,5.
По условию скорость с горы выше, поэтому k > 1, значить выбираем корень k = 7.
Ответ: в 7раз.
6. Электропоезд, двигаясь равномерно со скоростью 63 км/ч проезжает мимо платформы, длина которой 600 м. За 1 мин и 2с. Найдите длину электропоезда.
Решение:
Переведем вначале скорость в м/с, а время в секунды: 63км/ч = ![]() = = 17.5 м/с, 1мин 2 с = 62с.
= = 17.5 м/с, 1мин 2 с = 62с.
Пусть х км – длина поезда. Расстояние, пройденным поездом, складывается из длины поезда и длины платформы. Составим и решим уравнение:
х
+ 600 = 17,5 ![]() 62,
62,
х = 485.
485 м длина поезда.
Ответ: 485.
7. Путь от поселка до озера идёт сначала горизонтально, а затем в гору. Велосипедист доехал до озера и вернулся обратно. На горизонтальных участках пути он ехал со скоростью 2км/ч, на подъёме – со скоростью 8км/ч, а на спуске –со скоростью 15км/ч. Путь от поселка до озера занял у него 1 час, а обратный путь – 46 мин. Найдите расстояние от поселка до озера.
Решение: пусть х км –длина горизонтального участка, а у км – длина спуска (подъёма). Составим таблицу:
|
|
Расстояние |
Время |
|
Горизонтальный участок |
х км/ч |
|
|
Спуск |
у км/ч |
|
|
Подъём |
у км/ч |
|
Составим и решим систему уравнений:
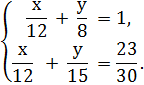
Ответ: 10 км.
Задачи для самостоятельного решения:
1. Путь от А до В в 90км мотоциклист проехал с постоянной скоростью. Обратно из В в А он ехал со скоростью на 12км/час больше, чем из А в В. В результате на путь из В в А он потратил на 15 минут меньше, чем из А в В. Найдите скорость мотоциклиста на обратном пути.
Ответ: 72.
2. Автомобилист планировал приехать из города на дачу, расстояние между которыми равно 80 км, к определенному сроку. Однако из-за поломки машины он выехал из города на 20 минут позже. Чтобы приехать на дачу вовремя, он увеличил скорость на 20км/час. С какой скоростью автомобилист ехал после ремонта машины?
Ответ: 80.
3. На 60 км пути велосипедист тратит на 4 часа больше времени, чем мотоциклист. Если он увеличит скорость на 3 км/ч, то на тот же путь потратит в 4 раза больше времени, чем мотоциклист. Найдите скорость велосипедиста.
Ответ: 12.
Задачи на движение по воде. Практикум по решению задач .
Особенности движение по воде является «присутствие» скорости течения реки.
Решим задачу 1. Из пункта А вниз по реке отправился плот. Одновременно навстречу ему из пункта В вышел катер. Через 2 часа он встретились. Прибыв в пункт А, катер сразу же отравился обратно. Сможет ли плот прибыть в пункт В раньше катера. Если скорость течения равна 3 км/ч, а расстояние АВ равно16 км?
Анализ. Скорость плота равна скорости течения. Очень важным условием, которое скрыто в этой задаче, является то, что и плот и катер движутся без остановок ( даже в момент встречи). Данная задача фактически состоит из двух задач.
№1. Из двух пунктов, расстояние между которыми равно 16км, одновременно навстречу друг другу вышли два объекта (плот и катер), которые встретились через 2 часа. Найдите скорость катера, если скорость плота 3 км/ч.
№2. Сравните время движения двух объектов, если известны их скорости и пройденный путь.
Обе задачи довольно просты и и могут быть решены арифметическим способом.
№1. Пусть х км/ч – собственная скорость катера. Скорость сближения плота и катера при движении навстречу друг другу в данном случае составляет (3+ (х - 3))км/ч или (16 : 2)км/ч. Получим уравнение 3+ (х - 3) = 8, х = 8.
Т.е. собственная скорость катера – 8км/ч.
№2. Катер плывет против течения 16 км со скоростью (8 – 3)км/ч и 16 км по течению со скоростью (8 + 3)км/ч. Он затратил на весь путь
16
: (8 - 3 ) + 16 : (8 + 3) = 4 ![]() (ч).
(ч).
Плот
плывет 16 км со скоростью 3 км\ч за ![]() часа, то есть за 5
часа, то есть за 5 ![]() (ч).
(ч).
Так
как 4
![]() < 5
< 5 ![]() , то плот не успеет прибыть в пункт В
раньше, чем туда вернётся катер.
, то плот не успеет прибыть в пункт В
раньше, чем туда вернётся катер.
Ответ: не сможет.
Задача 2.
Моторная лодка прошла 80 км от пункта А до пункта В и после трехчасовой стоянки вернулась обратно, затратив на весь путь 12 часов. Найдите скорость лодки в неподвижной воде (в км/ч). если скорость течения реки 2 км/ч.
Решение:
Пусть х км/ч –скорость лодки в неподвижной воде (х>2), тогда время
затраченное лодкой на путь по течению, равно ![]() , а время затраченное лодкой на путь против
течению,
, а время затраченное лодкой на путь против
течению,![]() равно
равно ![]() . Составим по условию задачи уравнение
. Составим по условию задачи уравнение ![]() +
+ ![]() + 3 = 12, откуда х = 18.
+ 3 = 12, откуда х = 18.
Ответ: 18.
Задача 3.
Весной
катер идет против течения реки в 2 раза медленнее, чем по течению. Летом
течение становится на 2 км/ч медленнее. Поэтому катер летом идёт против
течения в 1 ![]() раза медленнее, чем по течению. Найдите
скорость катера (в км\ч).
раза медленнее, чем по течению. Найдите
скорость катера (в км\ч).
Решение:
Обозначим собственную скорость катера за х км/ч, а у км/ч скорость течения реки весной, тогда скорость лодки по течению весной – (х + у) км/ч , а против течения реки - (х - у) км/ч. По условию задачи весной скорость по течению больше скорости против течения в 2 раза. Составим первое уравнение
2(х - у) = (х + у)
Скорость течения летом - (у - 2)км\ч, тогда скорость лодки по течению летом – (х + у - 2) км/ч, а против течения реки - (х – у +2) км/ч. По условию задачи летом скорость по течению больше скорости против течения в 1,4 раза Составим второе уравнение 1,4(х – у + 2) = (х + у - 2).
Решим
систему уравнений: ![]()
![]()
12 км/ч собственная скорость катера,
Ответ: 12.
Задачи для самостоятельного решения
Задача 1.
Моторная лодка в 4.00 вышла из пункта А в пункт В, расположенный в 126 км от А. Пробыв в пункте В 2 часа, лодка отправилась назад и вернулась в пункт А в 22.00. Определите (в км/ч) собственную скорость лодки, если известно, что скорость течения реки 2 км/ч.
Ответ: 16.
Задача 2.
Катер прошёл против течения реки 120 км и вернулся в пункт отправления , затратив на обратный путь на 4 часа меньше. Найдите скорость катера в неподвижной воде (в км/ч). если скорость течения реки 4 км/ч.
Ответ: 16.
Задача 3.
Расстояние между пристанями А и В равно 60 км. Из А в В по течению реки отправился плот, а через час вслед за ним отправилась моторная лодка, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К тому времени плот прошел 36 км. Найдите скорость лодки в неподвижной воде (в км/ч). если скорость течения реки 4 км/ч. Ответ дайте в км/ч.
Ответ: 16.
Движение по кругу. Практикум по решению задач.
Продолжаем рассматривать задачи на движение. Есть группа задач, которая отличается от обычных задач на движение – это задачи на круговое движение (круговая трасса, движение стрелок часов). Такие задачи и рассмотрим. Принципы решения те же самые, что и для закона прямолинейного движения. Но есть небольшие нюансы в подходах к решению.
Задача 1.
Бегун и велосипедист стартуют из одной точки по круговой дорожке в разные стороны. Когда бегун пробежал 150 м, он в первый раз встретился с велосипедистом. Какой путь проделал бегун до второй встречи? до десятой?
Решение:
Спортсмены стартуют в разные стороны. Каждое место встречи можно считать местом нового старта в разные стороны ( S0 – точка действительного старта).
Пусть Si – точка i –й встречи. Очевидно, S0 Si = 150 ∙ i (путь бегуна до i -ой встречи).
S0 Si =300; S0 Si =1500.
Ответ: 300 и 1500.
Задача 2.
Бегун и велосипедист стартуют из одной точки по круговой дорожке в разные стороны. Когда бегун пробежал 150 м, он в первый раз встретился с велосипедистом. Когда бегун бежал третий круг и находился в точке противоположной точке старта, он встретился с велосипедистом в десятый раз. Во сколько раз скорость велосипедиста больше скорости бегуна?
Решение 1 :
S0 S10 =150 ∙ 10=1500 (см. выше).
Пусть С – длина беговой дорожки. Тогда 150 ∙ 10 = 2,5 ∙ С, 150 ∙ 4 = С.
Пока бегун пробегает 150 м, велосипедист проезжает остальную часть круговой дорожки: 150 ∙ 4 – 150 = 150 ∙ 3.
Поэтому отношение
скоростей велосипедиста и бегуна k = ![]() = 3.
= 3.
Ответ: в 3 раза.
Решение 2:
На каждом полном
круге, сделанном бегуном, происходят 4 встречи (S0 = S4). Следовательно
длина круговой дорожки С =150 ∙ 4, а отношение скоростей спортсменов k = ![]() = 3.
= 3.
Можно заметить, что число 150 исключилось при вычислениях (вместо него может быть любое другое число). И в другой задаче его можно проигнорировать.
Решение 3:
Когда бегун сделал 5 полукругов. Произошла десятая встреча спортсменов, а вторая встреча произошла, когда бегун пробежал пол круга.
Следовательно, до
первой встречи бегун преодолел четверть круга,а велосипедист – остальные ![]() круга. Поэтому скорость велосипедиста
втрое выше.
круга. Поэтому скорость велосипедиста
втрое выше.
Решение 4:
До первой встречи
бегун преодолел расстояние S0 S1 = ![]() =
= ![]() , а велосипедист - С -
, а велосипедист - С - ![]() С =
С = ![]() С.
С.
Следовательно, k = ![]() С :
С :![]() С = 3.
С = 3.
Задача 3.
Бегун и велосипедист стартуют из одной точки по круговой дорожке в разные стороны. Когда бегун пробежал 150 м, он в первый раз встретился с велосипедистом. Когда бегун бежал третий круг и находился в точке противоположной точке старта, он встретился с велосипедистом в восьмой раз. Во сколько раз скорость велосипедиста больше скорости бегуна?
Решение 1 :
S0 S10 =150 ∙ 8 =
2,5 ∙ С, С = ![]() = 480,
= 480,
Пусть С – длина беговой дорожки. Тогда 150 ∙ 10 = 2,5 ∙ С, 150 ∙ 4 = С.
k = ![]() =
= ![]() .
.
Поэтому отношение
скоростей велосипедиста и бегуна k = ![]() .
.
Ответ: ![]() .
.
Задача 4.
Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля 80 км/ч, и через 40 мин после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля (в км/ч).
Решение:
Пусть х км/ч
скорость второго автомобиля
(х < 80), 40 мин =![]() часа. Разница в пройденном пути автомобилей составила 14 км
или (
часа. Разница в пройденном пути автомобилей составила 14 км
или (
![]() 80 -
80 -![]()
![]() х) км. Решая
уравнение (
х) км. Решая
уравнение ( ![]() 80 -
80 -![]()
![]() х) = 14,
получим х = 59.
х) = 14,
получим х = 59.
Ответ: 59.
Задача 5.
Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут они встретятся в первый раз. Если скорость одного из них на 21 км/ч больше скорости другого.
Решение:
Пусть х км/ч
скорость первого мотоцикла, тогда скорость второго мотоцикла (х + 21)км/ч,а
t – время движения.
Разница в пройденном пути мотоциклов составила (14 : 2 = 7) км или ( (x + 21)![]() t - xt )км. Решая уравнение
(x + 21)
t - xt )км. Решая уравнение
(x + 21)![]() t - xt = 7 , получим t =
t - xt = 7 , получим t = ![]() ч = 20мин.
ч = 20мин.
Ответ: 20.
Задачи для самостоятельного решения.
Задача 1.
Бегун и велосипедист стартуют из одной точки по круговой дорожке в разные стороны. Когда бегун бежал третий круг и находился в точке противоположной точке старта, он встретился с велосипедистом в восьмой раз. Во сколько раз скорость велосипедиста больше скорости бегуна? Где произойдет 2000 – я встреча спортсменов?
Ответ: ![]() . S0 S2000 =
625С.(произойдет на старте)
. S0 S2000 =
625С.(произойдет на старте)
Задача 2.
Бегун и велосипедист стартуют из одной точки по круговой дорожке в разные стороны. Когда бегун пробежал m кругов, он встретился с велосипедистом в n - й раз. Во сколько раз скорость велосипедиста больше скорости бегуна?
Ответ: ![]() .
.
Задача 3.
Бегун и велосипедист стартуют из одной точки по круговой дорожке в одном направлении. Когда бегун пробежал m кругов, он встретился с велосипедистом в n - й раз. Во сколько раз скорость велосипедиста больше скорости бегуна?
Ответ: ![]() .
.
Вывод. Отношение
скоростей велосипедиста и бегуна при старте в разные стороны равно ![]() , а при старте в одном направлении -
, а при старте в одном направлении - ![]() .
.
Задача 4.
Двум гонщикам предстоит проехать 85 кругов по кольцевой трассе протяженностью 8 км. Оба гонщика стартовали одновременно, а на финиш первый пришёл раньше второго на 17 минут. Чему равна средняя скорость второго гонщика, если известно, что первый гонщик в первый раз обогнал второго на круг через 48 минут ? Ответ дайте в км/ч.
Ответ: 150.
Задача 5.
Из пункта А круговой трассы выехал велосипедист, а через 40 мин следом за ним отправился мотоциклист. Через 8 минут после отправления он догнал велосипедиста в первый раз, а ещё через 36 минут после этого догнал его во второй раз.Найдите скорость мотоциклиста (в км/ч), если длина трассы равна 30 км.
Ответ: 60.
Тема IV. Решение задач на работу
Задачи на работу обычно содержат следующие величины:
t – время, в течение которого производится работа,
v – производительность труда, работа, произведенная в единицу времени (скорость выполнения работы);
A– работа, произведенная за время t .
Уравнения, связывающие эти три величины:
A = vt, t = ![]() , v=
, v= ![]() .
.
Практикум по решению задач .
Решим задачу 1:
При одновременной работе двух насосов пруд был очищен за
2 ч 55 мин. За сколько времени мог бы очистить пруд каждый насос, работая отдельно, если один из них может эту работу выполнить на 2 ч быстрее другого?
Решение: Пусть х ч – время выполнения работы второго насос, работая отдельно, тогда первый затратит - (х - 2)ч. (х >2)
Вся работа принимается за 1.
Производительность
труда первого насоса - ![]() , а второго -
, а второго - ![]() .
.
Совместная
производительность труда - (![]() +
+ ![]() ) или
) или ![]() .
.
Составим и решим
уравнение: ![]() +
+ ![]() =
= ![]() .
.
Ответ: 5 и 7 .
Задача 1. Одна из дорожных бригад может заасфальтировать некоторый участок дороги на 4 ч быстрее, чем другая. За сколько часов может заасфальтировать участок каждая бригада, если известно, что за 24 ч совместной работы они заасфальтировали 5 таких участков.
Пусть х ч – время работы первой бригады, работая отдельно,
тогда время второй - (х - 4 )ч.
Вся работа принимается
за 1. Составим
и решим уравнение: ![]()
(![]() +
+ ![]() )
) ![]() 24 =
24 = ![]()
Ответ: 8, 2.
Задача 2. На строительстве работали две бригады. После 5 дней совместной работы вторую бригаду перевели на другой объект. Оставшуюся часть работы первая бригада закончила через 9 дней. За сколько дней могла бы выполнить всю работу каждая бригада, работая отдельно, если известно, что второй бригаде на выполнение всей работы потребовалось бы на 12 дней меньше, чем одной первой бригаде?
Пусть х ч – время работы первой бригады, если она будет работать отдельно, тогда второй - (х - 12)ч.
Вся работа
принимается за 1. Составим
и решим уравнение: ![]()
(![]() +
+ ![]() )
) ![]() 5 +
5 + ![]()
![]() 9 =
9 = ![]() 1, х2 –
3х + 168 = 0, х = 24. (7 не удовлетворяет условию задачи, 7< 12).
1, х2 –
3х + 168 = 0, х = 24. (7 не удовлетворяет условию задачи, 7< 12).
Ответ: 24; 12.
Задача
3. Два ноутбука, работая совместно, выполняли определенный объем работы. Когда
первый проработал 2 часа, а второй 5 часов, оказалось, что они выполнили
половину работы. После того, как они проработали ещё 3 часа, им осталось
выполнить ![]() всей работы. За какое время каждый
ноутбук выполнит всю работу?
всей работы. За какое время каждый
ноутбук выполнит всю работу?
Решение:
Примем объем работы за 1. Пусть производительность первого ноутбука х, а второго – у. Когда первый проработал 2 часа, то объём его работы составил 2х, а второй проработал 5 часов и сделал 5у. Вместе их объём составил
( 2х+5у) или половину работы. Получим уравнение:
2х+ 5у = 0,5. (1)
После
этого ноутбуки проработали ещё 3 часа, т.е. первый проработал 2+3=5 часов и
выполнил 5х объёма работы, а второй проработал 5 + 3 = 8 часов и выполнил 8у
объёма работы. Вместе они выполнили (5х + 8у) или ![]() всей работы. Получим уравнение:
всей работы. Получим уравнение:
5х
+ 8у = ![]() . (2)
. (2)
Решим
систему уравнений (1) и (2):![]()
Умножим первое уравнение на 5, а второе – на 2 и вычтем из первого уравнения второе:
9у = 0,6 ,
2х = 0,5 - 5у.
y = 0,6:9 ,
y = 0,25 - 2,5у.
y = ![]() , х =
, х = ![]() .
.
Время работы – величина, обратно пропорциональная производительности, тогда время выполнения работы первым ноутбуком равно 12 часам, а вторым – 15часам.
Ответ: 12 и 15.
Задача 4 . Мастер и ученик изготовили в день 100 деталей. Во второй день мастер изготовил на 20% больше, а ученик – на 10% больше, чем в первый день. Всего во второй день мастер и ученик изготовили 116 деталей. Сколько деталей изготовил мастер и сколько изготовил ученик.
Решение:
Пусть х дет. изготавливал в первый день мастер, а у дет. изготавливал - ученик. Во второй день мастер изготовил – 1,2 х дет., а ученик изготовил – 1,1 х дет. Составим и решим систему равнений:
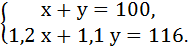
Ответ: 40; 60.
Задачи для самостоятельного решения
1. Два экскаватора, работая одновременно, выполняют некоторый объем земляных работ за 3 ч 45 мин. Один экскаватор, работая отдельно, может выполнить этот объем работ на 4 ч быстрее, чем другой. Сколько времени требуется каждому экскаватору в отдельности для выполнения того же объема земляных работ?
Ответ: 10 и 6 .
2. Чтобы наполнить бассейн, сначала открыли одну трубу и через 2 ч, не закрывая её, открыли вторую. Через 4 ч совместной работы труб бассейн был наполнен. Одна вторая труба могла бы наполнить бассейн в 1,5 раза быстрее, чем одна первая. За сколько часов можно наполнить бассейн через каждую трубу?
Ответ: 12 и 8.
3. Бригада слесарей может выполнить некоторое задание по обработке деталей на 15 ч быстрее, чем бригада учеников. Если бригада учеников отработает 18 ч, выполняя это задание, а потом бригада слесарей продолжит выполнение задания в течение 6 ч, то и тогда будет выполнено только 0,6 всего задания. Сколько времени требуется бригаде учеников для самостоятельного выполнения данного задания?
Ответ: 45.
4. Бассейн наполняется через первую трубу на 5 ч быстрее, чем через вторую. Бассейн можно наполнить, если открыть сначала первую трубу на 5 ч, а затем вторую на 7,5 ч. За сколько часов наполнится бассейн при совместной работе обеих труб?
Ответ: 6.
Итоговая контрольная работа
1-уровень.
1. После реконструкции завод увеличил выпуск продукции на 10%, а после замены оборудования еще на 30%. На сколько процентов увеличился первоначальный выпуск продукции?
Ответ: на 43%.
2.
Двое
рабочих, работая вместе, выполнили работу за 2 дня. Сколько времени нужно
каждому из них на выполнение всей работы, если известно, что если бы первый
проработал 2 дня, а второй один, то всего было бы сделано ![]() всей работы.
всей работы.
Ответ: 3 и 6.
3. Первые два часа автомобиль ехал со скоростью 55км/ч, следующий час - со скоростью 70 км/ч, а затем три часа - со скоростью 90 км/ч. Найдите среднюю скорост ь (в км/ч) автомобиля на протяжении всего пути.
Ответ: 75.
2-уровень.
1. Число 50 трижды увеличили на одно и то же число процентов, а потом уменьшили на это же число процентов. В результате получили число 69,12. На сколько процентов увеличивали, а потом уменьшали данное число?
Ответ: на 20%
2. Однотипные детали обрабатываются на двух станках. Производительность первого станка на 40% больше производительности второго. Сколько деталей было обработано за смену каждым станком, если первый работал в эту смену 6 ч, а второй – 7 ч, причем вместе они обработали 616 деталей?
Ответ: 336 ; 280.
3. Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 20 км. Через сколько минут они встретятся в первый раз, если скорость одного из них на 12 км/ч больше скорости другого.
Ответ: 16.
3-уровень.
1. Банк начисляет ежегодно 7% от суммы вклада. Найдите наименьшее число лет, за которое вклад вырастает более чем на 20%.
Ответ: 3 года
2. Турист идет из одного города в другой, каждый день проходя больше, чем в предыдущий день , на одно и то же расстояние. Известно, что за первый день турист прошел 10 километров. Определите сколько километров прошел турист в третий день, если весь путь он прошел за 6 дней, а расстояние между городами составляет 120 км.
Ответ: 18.
3. Двое
рабочих выполнили вместе некоторую работу за 6 дней. Если бы сначала первый
рабочий выполнил третью часть работы, а потом второй рабочий выполнил бы
оставшуюся часть работы, то вся работа была бы выполнена за 13![]() дня. За какое время первый рабочий мог
бы в одиночку выполнить всю работу, если известно, что его производительность
труда выше, чем производительность труда второго рабочего.
дня. За какое время первый рабочий мог
бы в одиночку выполнить всю работу, если известно, что его производительность
труда выше, чем производительность труда второго рабочего.
Ответ: 10.
Задачи на движение протяженных тел
Протяженными будем считать тела, длина которых соизмерима с расстоянием, которое они проезжают.
В задачах на движение протяженных тел обычно требуется определить длину одного из них. Наиболее типичные ситуации, предлагаемые в таких задачах, - определить длину поезда проезжающего мимо:
Помним, что во всех задачах на движение используется только одна
формула: это формула пути ![]()
Если поезд движется мимо столба, то он проходит расстояние равное его длине. Обозначим:
l – длина поезда,
v – скорость поезда,
![]()
Если поезд движется мимо протяженной лесополосы (платформы), то он проходит расстояние равное сумме длины самого поезда и лесополосы. Обозначим:
l1 – длина поезда,
l2 – длина лесополосы (платформы),
v – скорость поезда,
![]()
Если поезд движется мимо движущегося человека, то учитываем направление движения человека. Если он движется навстречу, то скорости складываются, если в одну сторону, то находим разность скоростей. Обозначим:
l – длина поезда,
v1 – скорость поезда,
v2 – скорость человека,
В одну сторону: ![]()
В разные стороны: ![]()
Если поезд движется мимо движущегося поезда, то учитываем направление движения второго поезда. Если он движется навстречу, то скорости складываются, если в одну сторону, то находим разность скоростей. Обозначим:
l1 – длина первого поезда,
l2 – длина второго поезда,
v1 – скорость первого поезда,
v2 – скорость второго поезда,
В одну сторону: ![]()
В разные стороны: ![]()
Рассмотрим несколько задач.
Задача 1. Поезд, двигаясь равномерно со скоростью 60км/ч, проезжает мимо придорожного столба за 30 секунд. Найти длину поезда в метрах.
Решение:
v = 60 км/ч = 1000 м/мин, t = 30 сек. = 1/2
мин. Длину поезда находим как пройденное расстояние: ![]()
Ответ: 500 метров.
Задача 2. Поезд, двигаясь равномерно со скоростью 90 км/ч, проезжает мимо лесополосы, длина которой равна 800 метрам, за 1 минуту. Найти длину поезда в метрах.
Решение:
v = 90 км/ч = 1500 м/мин, t = 1 мин. Тогда
пройденное поездом расстояние: ![]()
Это собственная длина поезда плюс длина лесополосы. Длина поезда равна: 1500 – 800 = 700 (м).
Ответ: 700 метров.
Задача 3. По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 90 км/ч и 30 км/ч. Длина товарного поезда равна 600 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 1 минуте. Ответ дайте в метрах.
Решение: Так как поезда двигаются в одном направлении, их относительная скорость равна:
v = 90 – 30 = 60 км/ч = ![]()
За 60 секунд один поезд проходит мимо другого, то есть преодолевает расстояние:
![]()
Это длина пассажирского и товарного поездов. Тогда длина пассажирского поезда равна:
1000 – 600 = 400 (м).
Ответ: 400 метров.
Задача 4. По двум параллельным железнодорожным путям навстречу друг другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 65 км/ч и 35 км/ч. Длина пассажирского поезда равна 700 метрам. Найдите длину скорого поезда, если время, за которое он прошёл мимо пассажирского поезда, равно 36 секундам. Ответ дайте в метрах.
Решение: Так как поезда двигаются в противоположных направлениях, их относительная скорость равна:
v = 65 + 35 = 100 км/ч = ![]()
За 36 секунд один поезд проходит мимо другого, то есть преодолевает расстояние:
![]()
Это расстояние, равное сумме длин обоих поездов. Значит, длина скорого поезда равна:
1000 – 700 = 300 (м).
Ответ: 300 метров.
Задача 5. Поезд проходит мимо неподвижного наблюдателя за 7 секунд, а мимо платформы длиной 378 метров – за 25 секунд. Найдите длину поезда.
Решение: Из первого условия следует, что за 7 секунд поезд проедет расстояние, равное собственной длине поезда. За 25 же секунд ему надо проехать собственно саму длину платформы, т.е. 378 метров и ещё надо «вытащить» головной вагон вперед на расстояние, равное длине поезда.
1) 25 – 7 = 18 (с) – время, за которое поезд проехал 378 м
2) 378 : 18 = 21 (м/с) – скорость поезда
3) 21 ![]()
Ответ: 144 м.
Задача 6. По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и скорый поезда. Скорый поезд, двигаясь со скоростью 120 км/ч, догнал пассажирский поезд и прошёл мимо него за 100 секунд. Найдите скорость пассажирского поезда, если его длина составляет 800 метров, а длина скорого поезда – 700 метров. Ответ дайте в км/ч.
Решение: Считаем, что пассажирский поезд неподвижен, а скорый приближается к нему со скоростью, равной разности скоростей поездов.
1) 700 + 800 = 1500 (м) – прошёл скорый поезд за 100 секунд
2) 1500 : 100 = 15 (м/с) – разность скоростей (скорость вдогонку)
15 м/с =![]() км/ч
= 54 км/ч
км/ч
= 54 км/ч
3) 120 – 54 = 66 (км/ч) – скорость пассажирского поезда.
Ответ: 66 км/ч.
Задача 7. По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 110 метров, второй — длиной 90 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 1000 метров. Через 16 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 400 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?
Решение: Пока сухогрузы перейдут из первого положения во второе, второй сухогруз переместился относительно первого на
1000 + 110 + 90 + 400 = 1600 (м).
Пусть v — разность скоростей сухогрузов, тогда
v = 1600 : 16 = 100 м/мин = 6 км/ч.
Ответ: на 6 км/ч.
Литература:
1. Алгебра 7 класс: учебник для общебразовательных учреждений
/ [Ю.H.Макарычев, Н.Г. Миндюк, К.И.Нешков, С.Б.Суворова ]; под ред.С. А.Теляковского - М, Прсвещение, 2013.
3. Решение задач и выполнение заданий по математике с комментариями и ответами для подготовки к ЕГЭ/ В.Н. Студенецкая, З.С. Гребнева.- Волгоград: Учитель,2005.
4. Подготовка к ЕГЭ по математике в 2012 году. Методические указания/ Ященко И. В., Шестаков С. А.. Трепалин А.С. . Захаров П. И. – М. :МЦНМО, 2012
5. Математика. 9-й класс. Подготовка к ОГЭ-2017: учебно-методическое пособие/ под ред. Ф.Ф. Лысенко, С.Ю. Кулабухова. – Ростов-на-Дону: Легион, 2016.
6. Уроки математическоко творчества / Ю. М. Куликов. – М. Просвещение,2005
7. Журнал «Математика в школе» № 3, 2017, стр 58-68.
8. Сетевые ресурсы:
9. Портал информационной поддержки Единого государственного экзамена
http://ege.edu.ru
http://alexlarin.net/
http://www.fipi.ru/
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.