Программа курса "Математика" для заочного отделения в СПО

Введение

Знания, приобретаемые студентом в результате изучения математики, играют важнейшую роль в процессе его обучения в техникуме, колледже. Они необходимы для успешного усвоения общетеоретических и специальных дисциплин в области экономики, статистики, менеджмента, бизнеса и информационных технологий. Математические методы широко используются для решения самых разнообразных задач техники, экономики и финансов, планирования и прогнозирования и многих других. Поэтому студент не должен забывать, что и после окончания среднего заведения он не раз столкнётся с необходимостью применения математики в практической деятельности.

Учебные планы экономических специальностей, а также механизации сельского хозяйства и технологии машиностроения предусматривают изучение курса «Математика».

Объём и содержание этого курса определяются программой, утверждённой Учебно-методическим управлением общего и профессионального образования Российской Федерации и не зависит от формы обучения (дневной, заочной).

Данное пособие соответствует учебной программе по курсу математики и является помощником для решения ряда задач. Здесь также представлена программа курса «Математика» и контрольные задания для студентов второго курса заочного отделения, охватывающие разделы: математический анализ, основы дискретной математики, основы теории вероятности и математической статистики, основные численные методы. Разобраны примеры решения наиболее трудных типовых задач, приведён список рекомендуемой литературы.

Программа курса «Математика»

1.     Определение предела функции. Бесконечно большие и бесконечно малые функции. Связь между бесконечно большими и бесконечно малыми функциями. Теоремы о пределах.

2.     Первый и второй замечательные пределы.

3.     Бесконечно малые функции и их свойства.

4.     Непрерывность функций. Непрерывность основных элементарных функций.

5.     Свойства непрерывных в точке функций. Непрерывность суммы, произведения и частного.

6.     Свойства функций, непрерывных на отрезке: ограниченность, существование наибольшего и наименьшего значений.

7.     Односторонние пределы. Точки разрыва функции и  их классификация.

8.     Производная функции. Её геометрический и механический смысл. Производная суммы, произведения и частного.

9.     Производная сложной функции. Производная обратной функции. Производные обратных тригонометрических функций.

10. Дифференцируемость функции. Дифференциал функции. Связь дифференциала с производной.

11. Теоремы о дифференцируемых функциях (Теоремы Ролля, Лагранжа, Коши).  Правило Лопиталя.

12. Производные и дифференциалы высших порядков.

13. Исследование поведения функций. Возрастание и убывание функций.

14. Необходимое и достаточное условие экстремума по первой производной.

15. Наибольшее и наименьшее значение функции на отрезке.

16. Выпуклость и вогнутость функции. Точки перегиба.

17. Асимптоты.

18. Общая схема исследования функции.

19. Численное дифференцирование. Формулы приближённого дифференцирования. Погрешность в определении производной.

20. Первообразная. Неопределённый интеграл и его свойства. Таблица основных формул интегрирования. Непосредственное интегрирование, интегрирование заменой переменной, интегрирование по частям.

21. Определённый интеграл. Основные свойства определённого интеграла. Формула Ньютона-Лейбница.

22. Замена переменных в определённом интеграле. Интегрирование по частям.

23. Приближённое вычисление определённого интеграла. Формулы прямоугольников, трапеций. Симпсона. Оценка погрешности.

24. Приложение интегралов к вычислению площадей плоских фигур, длин дуг кривых, объёмов тел вращений и площадей поверхностей вращения.

Контрольная работа.

1-10. Найти пределы функций, не пользуясь правилом Лопиталя.

1)      а);

            б);

             в);

             г) ;

2)      а);

            б);

            в);

            г) ;

3)      а);

            б);

            в);

            г) ;

4)      а);

           б);

           в);

            г) ;

5)      а);

      б) ;

      в) ;

      г) ;

6)      а);

      б) ;

      в) ;

      г) ;

7)      а);

      б) ;

      в) ;

      г) ;

8)      а) ;

            б) ;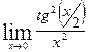

            в) ;

            г) ;

9)      а) ;

            б) ;

            в) ;

            г) ;

10)  а) ;

            б) ;

            в);

            г) ;

11-20. Найти производные данных функций.

11)  а);

      б) ;

      в) ;

12)  а) ;

      б) ;

      в) ;

13)  а);

      б) ;

      в) ;

14)  а) ;

            б);

            в);

15)   а);

      б) ;

      в) ;

16)  а) ;

      б) ;

      в) ;

17)  а) ;     

б) ;

      в) ;

18)  а) ;

     б) ;

     в) ;

19)  а) ;

     б) ;

     в) ;

20)  а) ; 

     б) ;

     в) ;

21-30. Найти предел функции, используя правило Лопиталя.

21)  а) ;

     б) ;

22)  а) ;

      б) ;

23)  а) ;

      б) ;

24)  а) ;

      б) ;

25)  а) ;

      б) ;

26)  а) ;

      б) ;

27)  а) ;

      б) ;

28)  а) ;

      б) ;

29)  а) ;

      б) ;

30)  а) ;

      б) ;

31-40. Найти  и .

31)  ;

32)  ;

33)  ;

34)  ;

35)  ;

36)  ;

37)  ;

38)  ;

39)  ;

40)  ;

41-50. Найти  наибольшее и наименьшее значение функции на отрезке .

41)  .

42)  .

43)  .

44)   .

45)  .

46)   .

47)   .

48)  .

49)  .

50)  .

51-60. Исследовать функцию методами дифференциального исчисления и, используя результаты исследования, построить её график.

51)  ;

52)  ;

53)  ;

54)  ;

55)  ;

56)  ;

57)  ;

58)  ;

59)  ;

60) 

61-70. Найти неопределённые интегралы.

61)  а);

      б) ;

      в) ;

62)  а) ;

      б) ;

      в) ;

63)  а) ;

      б) ;

      в) ;

64)  а) ;

      б) ;

      в) ;

65)  а) ;

      б) ;

      в) ;

66)  а) ;

      б) ;

      в) ;

67)  а) ;

      б) ;

      в) ;

68)  а) ;

     б) ;

     в) ;

69)  а) ;

     б) ;

     в) ;

70)  а) ;

      б) ;

       в);

81-90.

81. Вычислить площадь фигуры, расположенной в верхней полуплоскости и ограниченной линиями: , , .

82. Вычислить площадь фигуры, ограниченной линиями: , .

83. Вычислить площадь фигуры,  ограниченной линиями: , , .

84. Вычислить площадь фигуры, ограниченной линиями: , .

85. Вычислить площадь фигуры, ограниченной линиями: , .

86. Вычислить площадь фигуры, ограниченной линиями: , .

87. Вычислить площадь фигуры,  ограниченной линиями: , , .

88. Вычислить площадь фигуры,  ограниченной линиями: , , .

89. Вычислить площадь фигуры,  ограниченной линиями: , .

90. Вычислить площадь фигуры, ограниченной линиями: ,  .

91-100.

91. Вычислить объём тела вращения, образованного вращением вокруг оси ординат фигуры, расположенной в первой четверти и ограниченной линиями

, , .

92.  . Вычислить объём тела вращения, образованного вращением вокруг оси ординат фигуры,  ограниченной линиями

, .

93. Вычислить объём тела вращения, образованного вращением вокруг оси абсцисс фигуры, расположенной в первой четверти и ограниченной линиями

, , .

94.  Вычислить объём тела вращения, образованного вращением вокруг оси абсцисс фигуры,  ограниченной линиями

, .

95.  Вычислить объём тела вращения, образованного вращением вокруг оси абсцисс фигуры,  ограниченной линиями

,  , ,.

96. Вычислить объём тела вращения, образованного вращением вокруг оси абсцисс фигуры,  ограниченной линиями

, .

 97. Вычислить объём тела вращения, образованного вращением вокруг оси абсцисс фигуры,  ограниченной линиями

, , .

 98. Вычислить объём тела вращения, образованного вращением вокруг оси абсцисс фигуры,  ограниченной линиями

, .

 99. Вычислить объём тела вращения, образованного вращением вокруг оси абсцисс фигуры,  ограниченной линиями

, ,,  .

 100.  Вычислить объём тела вращения, образованного вращением вокруг оси абсцисс фигуры,  ограниченной линиями

, .

Методические указания к решению задач

Задача 1.

а) Найти предел функции , не пользуясь правилом Лопиталя.

Решение: В данном случае , при  числитель и знаменатель дроби являются бесконечно малыми функциями, такое отношение условно обозначают , представляет собой неопределённость, для её раскрытия сделаем следующие преобразования:

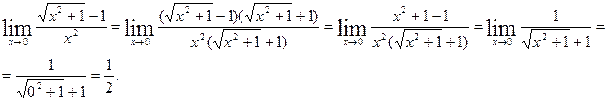
б) Найти предел функции , не пользуясь правилом Лопиталя.

Решение: В данном случае , при  числитель и знаменатель дроби являются бесконечно малыми функциями, такое отношение условно обозначают , представляет собой неопределённость, для её раскрытия сделаем следующие преобразования:

.

При вычислении заданного предела мы пользовались следующим результатом, называемым «первым замечательным пределом»:

, а также знаниями из тригонометрии , а также значением .

в) Найти предел функции .

Решение: В данном случае , при  числитель и знаменатель дроби являются бесконечно малыми функциями, такое отношение условно обозначают , представляет собой неопределённость, для её раскрытия сделаем следующие преобразования:

.

При вычислении заданного предела мы пользовались разложением квадратного выражения на множители:

.

Задача 2. Найти производные функций.

а) ;

Решение: ;

б) ;

Решение: ;

в) ;

Решение: ;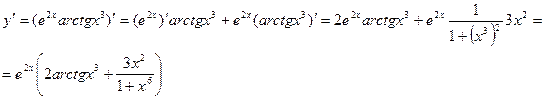

Задача 3.  С помощью правила Лопиталя вычислить предел функции .

Решение: Непосредственная подстановка  приводит к неопределённости вида , следовательно, можно применить правило Лопиталя: заменить предел отношения функций пределом отношения их производных.

Задача 4. Вычислить неопределённые интегралы.

а) ;

Решение: Полагая , , получим

;

б);

Решение: При вычислении этого интеграла надо применить  метод интегрирования по частям. Положив , , найдём: , .

Подставляя в формулу , получим

.

Задача 5. Вычислить площадь фигуры, ограниченной линиями , и параболой .

Решение: Найдём абсциссы точек пересечения прямой и параболой:

,

,

, .

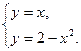
Воспользуемся формулой для вычисления площади фигуры, ограниченной двумя кривыми: .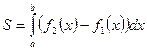

При , , , .

Получим, 

Задача 6. Вычислить объём тела, полученного в результате вращения вокруг оси Ох, фигуры ограниченной линиями , , , .

Решение: Объём тела вращения находим по формуле

.

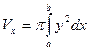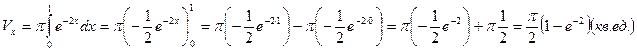
Литература:

1)    Баврин И.И. «Высшая математика»; М.: Академия, 2002.

2)    Богомолов Н.В. «Практические занятия по математике»; М.. 1999.

3)    Валуцэ И.И., Дилигул Г.Д. «Математика для техникумов»; М.: 1980.

4)    Выгодский М.Я. «Высшая математика для техникумов», Высшая школа, 1968.

5)    Высшая математика в упражнениях и задачах. В 2 ч. Учебное пособие для вузов/ П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова, С.П. Данко. – 6-е изд. – М.: ООО «Издательство Оникс»: ООО «Издательство «Мир и Образование». 2006.

6)    Демидович Б. П. «Краткий курс высшей математики»: Учеб. Пособие для вузов/ - М.: ООО «Издательство Астрель»; ООО «Издательство АСТ», 2003.

7)    Лунгу К.Н. «Сборник задач по высшей математике»; Рольф, М., 2001.

8)    Ильин В. А., Куркина А. В. «Высшая математика»: учеб. – 2-е изд., - М.: ТК Велби, издательство Проспект, 2007.

9)    Лурье Л.И. «Основы высшей математике: учебное пособие»; М.: Дашков и , 2002.

10)                       Письменный Д.Т. «Конспекты лекций по высшей математике»; 1-2ч., Рольф, М.; 2001.

11)                       Рогов А.Т. «Задачник по высшей математике для техникумов»; М.; 1973.

12)