Производная алгебраической суммы.

Определение производной.

Производная алгебраической суммы.

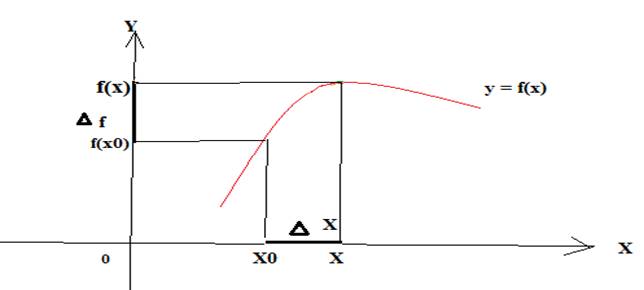
Определение. Производной функции f в точке x_o  называется предел, к которому стремится разностное отношение  при ,

стремящемся к нулю.

= X – X₀  - приращение независимой переменной ( или приращение аргумента),

X₀ – начальное значение аргумента,

X – новое значение аргумента,

- приращение аргумента.

f (X₀) – начальное значение функции,

f (X) – новое значение функции,

Df = f (X) - f (X₀) = f (X₀ +) - f (X₀) –приращение функции.

Производная функции f в точке X₀ обозначается f ¢( X₀ ).

(читается: Эф штрих от X₀ ).

Производную еще называют скоростью изменение функции в точке X_0.

Нахождение производной данной функции называется дифференцированием.

На основании определения производной выводятся правила дифференцирования.

Таблица производных.

1.   (C)΄= 0

2.   (X)΄ = 1

3.   ( KX + b)΄= K

4.   ( X²)΄ = 2X

5.   (Xⁿ)΄ = n∙X^n-1

6.   ( )΄= - 

7.  ()΄=

8.  (Sin x)΄= Cos x

9.   (Cos x)΄= - Sin x

10.  ( tgx)΄ =

11.  (Ctgx)΄=

12.  (C∙U)΄= C∙(U)΄

13.  (U±V)΄=U΄±V΄ 

14.  (U∙V)΄=U΄∙V+ U∙V΄

15.  ()΄=

16.  (f()∙φ

17.   (e^x) = e^x  , где   e ≈ 2,7

18.   (a^x)΄= ,где  

19.   ( x)΄=

20.  ( log_ax)΄=

Производная алгебраической суммы.

Задание 1.

Даны функции  f ( X ) = X ³  и ее производная  h ( X ) = 3X ²

 Как записать равенство этих двух функций с использованием производной?

Записать это равенство в тетрадь.

Задание 2.

Не вычисляя производных, заполните пропуски. Выполните в тетради.

1)   ( 3Х + Х³ )¢  = . . . + ( Х³ )¢

2)   ( 5 – Х⁷ + Sin X )¢  = ( 5 )¢  - . . . + . . .

3)   ( . . . – X )¢ = ( 2X ³ )¢ – (X )¢

4)   ÖX + . . . )¢ = . . . + (2COS X )¢

5)   ( 2X – X ⁵ + 4 )¢  = . . . - . . . + . . .

6)    ( . . . + . . . )¢ = ( 7X )¢ + ( 2tgX)¢

Задание 3.

Запишите в тетрадь правило нахождения производной суммы, заполняя пропуски.

Производная   . . .  функций, каждая из которых имеет  . . .  , равна сумме  . . .  этих функций.

Задание 4.

Запишите формулу, выражающую правило дифференцирования суммы функций, обозначив две функции буквами U  и  V. Найдите это правило в таблице производных.

Задание 5.

Найдите производные следующих функций:

( U ± V )¢ = . . .

1)       Y ¢  = ( X + 2 )¢ = . . .

2)     Y ¢= ( X ³ + X )¢ = . . .

3)     Y ¢ = (  + 5 – COS X ) ¢ = . . .

4)     Y ¢ = ( 1 – X )¢  = . . .

5)     Y ¢ = ( Sin X + tg X )¢  = . . .

6)     Y ¢ = ( X ²  + )¢  = . . .

7)     Y¢ = ( 1,7 – Ctg X + X )¢  = . . .

8)