Производная. Нахождение производной степенной функции, производной алгебраической суммы нескольких функций и производной произведения двух функций.

Производная. Нахождение производной степенной функции, производной алгебраической  суммы нескольких функций и производной произведения двух функций.

Определение. Производной функции f в точке x_o  называется предел, к которому стремится отношение  при ,

стремящемся к нулю.

= X – X₀  - приращение независимой переменной ( или приращение аргумента),

X₀ – начальное значение аргумента,

X – новое значение аргумента,

- приращение аргумента.

f (X₀) – начальное значение функции,

f (X) – новое значение функции,

Df = f (X) - f (X₀) = f (X₀ +) –приращение функции.

Производная функции f в точке X₀ обозначается f ¢( X₀ ).

(читается: Эф штрих от X₀ ).

Производную еще называют скоростью изменение функции в точке X_0.

Нахождение производной данной функции называется дифференцированием.

На основании определения производной выводятся правила дифференцирования.

Производная степенной функции с целым показателем.

1.    Производная постоянной.

Производная постоянной величины равна нулю.

( С ) ¢ = 0

(С – постоянная величина ).

Примеры.

( 5 ) ¢ = 0

( - ) ¢ = 0

( 8,5 )¢ = 0

2.    Производная степенной функции.

Производная степенной функции вычисляется по формуле:

( X ⁿ )¢= n× X ^n-1

( n- любое целое число. Х – любое число ¹ 0 ).

Примеры.

1. ( Х ⁵ )¢ = 5 Х ⁴

2. ( Х ⁸ )¢  = 8 Х ⁷

3. ( Х ^-3 ) = -3 Х ^-4 = -                                  

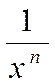
4.

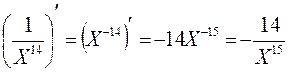
Выполните задания в тетради, заполнив пропуски:

1) (C )¢ = . . .                                    8)    (X )¢  = . . .

2)  (2 )¢  = . . .                                   9)    ( X ²)¢  = . . .

3)  ( - 4 )¢  = . . .                                10)   ( X ⁷ )¢  = . . .

4)   ( )¢  = . . .                             11)   ( X ^-8 )¢  = . . .

5)   ( - 0,18 )¢  =. . .                           12)   ()¢  = . . .

6)  ( . . .)¢  = 0                                   13)  ( . . . )¢  = 6 X⁵

7)  ( . . . )¢  = 0                                  14)  ( . . . )¢ = - 10 X ^-11

Производная алгебраической суммы.

Задание 1.

Даны функции  f ( X ) = X ³  и ее производная  h ( X ) = 3X ²

 Как записать равенство этих двух функций ?

Записать это равенство в тетрадь.

Задание 2.

Не вычисляя производных, заполните пропуски. Выполните в тетради.

1)   ( 3Х + Х³ )¢  = . . . + ( Х³ )¢

2)   ( 5 – Х⁷ + Sin X )¢  = ( 5 )¢  - . . . + . . .

3)   ( . . . – X )¢ = ( 2X ³ )¢ – (X )¢

4)   ÖX + . . . )¢ = . . . + (2COS X )¢

5)   ( 2X – X ⁵ + 4 )¢  = . . . - . . . + . . .

6)    ( . . . + . . . )¢ = ( 7X )¢ + ( 2tgX)¢

Задание 3.

Запишите в тетрадь правило нахождения производной суммы, заполняя пропуски.

Производная   . . .  функций, каждая из которых имеет  . . .  , равна сумме  . . .  этих функций.

Задание 4.

Запишите формулу, выражающую правило дифференцирования суммы функций, обозначив две функции буквами U  и  V. Найдите это правило в таблице производных.

Задание 5.

Найдите производные следующих функций:

( U ± V )¢ = . . .

1)     Y ¢  = ( X + 2 )¢ = . . .

2)     Y ¢= ( X ³ + X )¢ = . . .

3)     Y ¢ = (  + 5 – COS X ) ¢ = . . .

4)     Y ¢ = ( 1 – X )¢  = . . .

5)     Y ¢ = ( Sin X + tg X )¢  = . . .

6)     Y ¢ = ( X ²  + )¢  = . . .

7)     Y¢ = ( 1,7 – Ctg X + X )¢  = . . .

Производная произведения двух функций.

               ( U × V )¢  = U ¢ × V + U × V ¢                   ( ф. 1)

Следствие:         ( C × U ) ¢ = C × ( U ) ¢                       ( ф. 2 )

                                 (   C  - постоянная величина  )

Постоянный множитель можно выносить за знак производной.

Пример 1.  Найти производную произведения двух функций f(X)× g (X),

                    если          f(X) = X³ + X    и      g(X) = X ² – 2.

Решение.

f(x) ×g(X) = ( X³ + X) × (X² – 2)

обозначим   U = ( X³ + X) ,        V = ( X² – 2)

воспользуемся ф. 1.

(( X ³ + X) × (X² – 2)) ¢ = ( X³ + X)¢ ×(X² – 2) + ( X³ + X) ×(X² – 2)¢ =

((X³ )¢ + (X)¢)× (X² – 2) + ( X³ + X)× ((X² )¢  – ( 2 )¢) = (3X² + 1) ×(X² – 2) +

(X³ + X) × ( 2X - 0 ) =(3X² + 1) ×(X² – 2) +(X³ + X) ×  2X = 3X⁴ – 6X² +X² – 2 +2X⁴ + 2X² = 5X⁴ -3x² – 2.

Пример 2.  Найти производные.

воспользуемся ф. 2.

          y = 5COS X

y¢ = ( 5COS X )¢ = - 5Sin X

1)    y = 10X³ + 3X

y¢ = (10X³ + 3X )¢ = (10X³ )¢  +( 3X )¢ = 30X² + 3 × 1 =30X² + 3

          Задание для выполнения в тетради.

Заполните пропуски:

( C ×U )¢ = …                                                ( U × V )¢ = …

1)  ( 2 ×(2X + 1 ))¢ = …                                5) ((2X + 1) × X³)¢  = . . .

2) ( 3X ⁵ )¢  = . . .                                           6) (( X² – X) × (2X⁴ – 5))¢  = . . .

3) ( 18 Sin X ) ¢ = . . .                                   7) ( 4X⁵  × (3X² + 10)) ¢ =. . .

4) ( 0,6 tg X)¢ = . . .                                       8) ( 5X² × COS X )¢ = . . .