Поделиться
ч1.Произв. Примен.произв.Повтор.11кл.doc
Повторение. «Производная. Применение производной к исследованию функции».
11 класс. Часть 1.
Формулы производных и правила дифференцирования.
|
№ |
Функция |
Производная |
Примеры |
|
1 |
f(x)=C c-постоянная |
( С )′ = 0 |
1) ( 5 ) ′ =0; 2) (0,36) ′ = 0 ; 3) ( - 4,23) ′ =0; 4) ( ⅛ ) ′ =0. |
|
2 |
f(x)=Х |
(Х) ′ =1 |
|
|
3 |
f(x)=Хn |
(Хn) ′ = n ·Хn -1 |
1) ((X)2 ) ′ =2X ; 2) ((X)10 ) ′= 10 X9; 3) |
|
4 |
f(x)= |
( |
|
|
5 |
f(x)=√X |
(√X) ′ = |
|
|
6 |
f(x)=C·U |
(C·U) ′ = C·U ′ |
1) (5X3) ′= 15X2; 2) |
|
7 |
f(x)=Sin x |
(Sin x) ′ = Cos x |
1) (10 Sin x) ′ = 10Cos x |
|
8 |
f(x)=Cosx |
(Cos x) ′ = - Sin x |
1) (0,5Cos x) ′ = - 0,5Sin x |
|
9 |
f(x)=tg x |
(tg x) ′ = |
1) (18tg x) ′ = |
|
10 |
f(x)=ctg x |
(ctg x) ′ = - |
1) ( |
|
11 |
f(x)= ex |
(ex ) ′ = ex |
1) (9ex)′ = 9ex |
|
12 |
f(x)= ax |
(ax)′ = ax · ln a |
1) (5x)′ = 5x · ln 5 |
|
13 |
f(x)= ln x |
(ln x) ′ = |
1) (15 ln x) ′ = |
|
14 |
f(x)=logax |
(log a x)
′ = |
1) ( 12log 4
x) ′ = |
|
15 |
f(x)=U±V |
(U±V) ′ =U′ ± V′ |
1) ( 2x4+ 13x + 5Cos x+ 8) )=8x3 +13 -2Sin x |
|
16 |
f(x)= U·V |
(U·V) ′ = U′·V + U·V′ |
1) (( 4x5 +2)·Sin x) ′ =(4x5 +2)′· Sin x +(4x5 +2)· (Sin x) ′ =20x4 Sin x+(4x5 +2)· Cos x=20x4 Sin x+4x5 Cos x+2Cos x |
|
17 |
f(x)= |
( |
1)
= |
|
18 |
f(φ(x)) |
(f(φ(x))) ′= f′( x)·φ′ (x) |
1) ((7x2+3x5)3)´= 3·(7x2+3x5)2·(7x2+3x5)´ =3·(7x2+3x5)2·(14x + 15x4); 2) (Cos(5x4 – 3x2 +2)) ′= - Sin(5x4 – 3x2 +2) ·(5x4 – 3x2 +2) ′= - Sin(5x4 – 3x2 +2) ·(20x3 – 6x)= (6x - 20x3) · Sin(5x4 – 3x2 +2). |
Тема 1.Применение производной. Физический смысл производной.
Краткая теория.
Так как это физический смысл производной, то все обозначения будут как в физике, то есть S(t) - координата точки от времени (Это теперь так будет обозначаться заданная функция, которую раньше чаще всего мы обозначали f(x) );V(t) - скорость точки или тела ; a(t) - ускорение тела.
Правила нахождения производных будем использовать все те, которые мы записали в большой таблице в тетради.
Скорость V(t)равна производной от координатыS(t) по времени t.
Формула : V(t) = S´(t)
Ускорение a(t) равно производной от скорости V(t) по времени t.
Формула : a(t) = V´(t)
Примечание: Чтобы найти ускорение, если задана координата, надо сначала найти скорость, как производную от координаты и взять еще раз производную уже от найденной скорости.
Рассмотрим решенные примеры.
Пример 1. Точка движется прямолинейно по закону S(t) = 4t3 - 3t2+ 10 (м). Найти : а) скорость через 2 секунды; б) ускорение через 2 секунды; в) в какой момент времени ускорение станет равно нулю. Решение.
а) V(t) = S´(t)V(t) = (4t3 - 3t2 + 10)´ = 12t2 - 6t +0 =12t2 – 6t, приt=2 V(2) =12·22 - 6·2 = 48 – 12= 36 (м/с). Ответ: 36.
б) ищем ускорениеa(t) = V´(t)a(t)= (12t2 – 6t)´ =24t – 6, при t=2 a(t) = 24·2 – 6=42(м/c2).
Ответ: 42.
в) Так как ускорение имеет вид: a(t)=24t – 6, то 24t – 6 = 0 ; 24t = 6; t = 6 : 24= 0,25 сек. Ответ:0,25.
Пример 2. Точка движется прямолинейно по закону S(t) =0,5t2 +3t +2 (м). Через какой промежуток времени скорость станет равна 15 м/с. Решение.
V(t) = S´(t)V(t) = (0,5t2 +3t +2)´ =0,5·2t + 3= t + 3,по условию V(t) =15, t + 3 =15, t =15-3=12 (сек) Ответ: 12.
Пример 3. Тело движется прямолинейно по закону S(t) =4 + 8t – (2t3 / 3). Через сколько секунд тело остановится (то есть скорость станет равна нулю).Решение.
V(t) = S´(t)V(t) = (4 + 8t – (2t3 / 3))´ = 0+8 - 2·3t2/3= 8- 2t2,8- 2t2 = 0 2t2 =8 t2 =4 t = √4 t=2(cек).Ответ: 2.
Тема2. Применение производной Геометрический смысл производной.
Краткая теория.
Геометрический смысл производной связан с углом наклона касательной, проведенной к графику функции в данной точке или с угловым коэффициентом наклона касательной.
( Теория и разобранные примеры должны быть записаны в тетрадь)
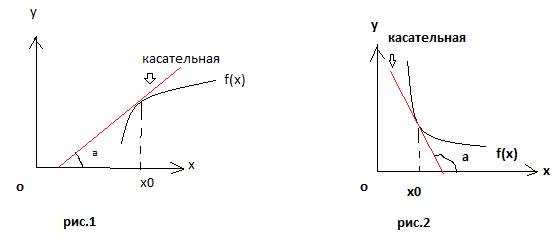
На рис.1 угол наклона касательной с положительным направлением оси ОХ – острый, а на рис.2 этот угол тупой. Если угол наклона касательной острый, то функция при увеличении значения переменной Х будет возрастать. Если угол наклона касательной тупой, как на рис.2, то функция на этом участке убывает.
Геометрический смысл производной:
1)f ´(x) = tgɑЗначение производной в заданной точке равно тангенсу угла наклона касательной, проведенной в заданной точке.
Или
2)f ´(x) =KЗначение производной в заданной точке равно угловому коэффициентуКнаклона касательной. (Так как касательная – это прямая линия, то ее уравнение имеет вид: y = k·x + b, где k =f ´ (x) )
Пример1. Вычислить тангенс угла наклона касательной к графику функции y= x - x3в точке с абсциссой Х0= - 2. Решение.
f ´(x) = tgɑy´ = (x – x3)´=1 – 3x2y´( - 2)= 1 - 3·(-2)2 = 1 – 12= - 11.Ответ: -11.
Пример2. Найти угловой коэффициент наклона касательной, проведенной к графику функции f(x) = 2Sinx + 3Cosxв точке х0 = π/2. Решение.
f ´(x) =Kf ´ (x) =(2Sinx + 3Cosx )´ = 2Cos x – 3Sin x
f ´ (π/2) =( 2Cos (π/2) – 3Sin( π/2) = 2·0 - 3·1 = -3.Ответ. -3
Пример3. Найти угол наклона касательной к графику функции y= - tgx, проходящую через точку М (π ;0). Решение.
f ´(x) = tgɑtg ɑ =y´ (х) = (- tgx )´ = - 1/ (Cos2 x ) из точки М (π ; 0) координатаx0=π (вторая координата не используется)подставим в найденную производную вместо х число π, тогда получим :
tg ɑ = -1 / Cos2π. Cosπ= -1 (таблица значений тригонометрических функций).
tg ɑ = -1 / ( -1)2 = -1/1 = -1 угол ɑ = 135° (таблица значений тригонометрических функций. Угол наклона касательной может быть в пределах 0°< ɑ<180°).Ответ: 135.
Пример4. На рисунке изображен график функции и касательные , проведенные к нему в точках с абсциссами A, B, C, D.
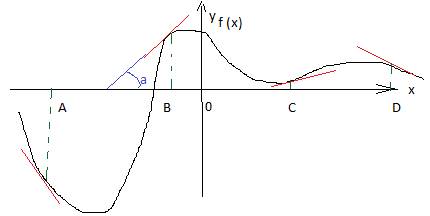В правом столбце указаны значения
производной функции в точках A, B,
C, D.Пользуясь графиком,
поставьте в соответствие каждой точке значение производной функции в ней.
|
ТОЧКИ |
ЗНАЧЕНИЯ ПРОИЗВОДНОЙ |
|
A |
1) – 1,8 |
|
B |
2) – 0,7 |
|
C |
3) 1,4 |
|
D |
4) 0,5 |
При решении заполните таблицу, расчерченную ниже, в которой для каждой точки укажите номер соответствующего значения производной.
|
A |
B |
C |
D |
|
|
|
|
|
(При записи ответа укажите полученное четырехзначное число).
Решение.
Пояснения к решению. Их можно в решении не писать только заполненную таблицу и ответ.(Пояснения даны для того, чтобы вы поняли, как решать такого типа задание).
Сначалаопределим знаки производной в каждой отмеченной точке. Для этого надо мысленно продолжить каждую касательную ( красная) до пересечения с осью ОХ ( как сделано синим цветом для точки B). Увидим, что в точке A угол наклона касательной будет тупой ( угол берем только с положительным направлением оси ОХ, куда указывает стрелка оси), в точке B этот угол острый, в точке С– острый, в точке D – тупой. Производная f ´(x) = tgɑЗначение производной в заданной точке равно тангенсу угла наклона касательной, проведенной в заданной точкеДля острых углов тангенс положительный, чем больше острый угол тем больше его тангенс.Для тупых углов тангенс отрицательный, чем больше тупой угол тем меньше значение его тангенса. В точках Bи С производная положительная, причем в т.Bострый угол больше , чем в т. С. Значит, в таблицу ответов под точкой B пишем цифру 3, под точкой С пишем цифру 4. В точках Aи D производная отрицательна, причем в т. А тупой угол больше, чем в т.D. В таблице ответов под точкой А пишем цифру1, под точкой D пишем цифру 2.
|
A |
B |
C |
D |
|
1 |
3 |
4 |
2 |
Ответ: 1342
Тема 3. Применение производной.
Исследование функции на возрастание и убывание (на монотонность).
Краткая теория. (Теория и разобранные примеры должны быть записаны в тетрадь).
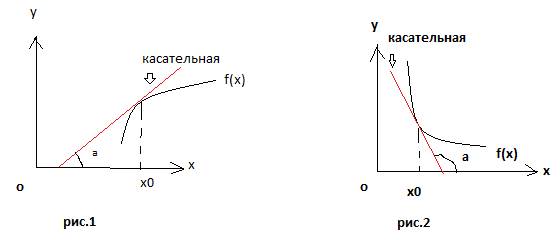
На рис.1 угол наклона касательной с положительным направлением оси ОХ – острый, а на рис.2 этот угол тупой. Если угол наклона касательной острый, это означает, что производнаяв этой точке положительна, и функция при увеличении значения переменной Х будет возрастать.( см. рис.1). Если уголнаклона касательной тупой, как на рис.2, это означает, что производная в это точке отрицательна, и функция на этом участке убывает. (см.рис. 2.). Итак, условие возрастания и убывания функции:
еслиf ´(x) > 0 на некотором промежутке, то функция возрастает на этом промежутке, если f ´(x)< 0 на некотором промежутке, то функция убывает на этом промежутке,
У функции может быть несколько участков убывания и
возрастания. Рис. 3.Разберем пример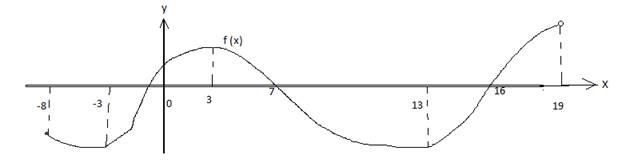
На
рис.3 изображен график некоторой функцииf (x). Функция возрастает на промежутках [-3;3] и [13;19).
На этих промежутках угол наклона касательной с положительным направлением оси
ОХ острый, значит производная f ´(x) >
0, так кактангенс острого угла положителен.Функция убывает
на промежутках [ -8; -3] и [3;13], так как на этих участках угол наклона
касательной с положительным направлением оси ОХ тупой, значит производная f
´(x) < 0, так кактангенс тупого угла
отрицательный.Если надо определить
участки возрастания и убывания не по графику, а путем вычислений, то действуют
по такому
плану:
1. Найти область определения заданной функции.
2. Найти производную f ´(x) заданной функции.
3. Найти промежутки, где производная f ´(x) > 0иf ´(x) < 0, ( решая полученные неравенства аналитически или методом интервалов).
Пример1. Исследовать функцию f(x) = 5x2 -3x +1на монотонность (на возрастание и убывание). Решение.
1. Область определения функцииD(f) = R.
2. f ´(x) = (5x2 -3x +1)´ = 10x – 3
3. f ´(x) = 0 10x -3 =0 10x=3 x= 0,3 Отметим найденную точку на числовой прямой. Числовая прямая разбилась на два промежутка (-∞; 0,3] и [0,3; + ∞).Проверим знак производной в каждом из полученных промежутков. Для этого выбираем любое произвольное число из левого промежутка и потом из правого. Выберем любое число х<0,3например, х=0 и подставим вместо х в производную, получим: 10·0 -3= -3< 0.Поставим слева от числа 0,3 знак минус на числовой прямой.Выберем любое число х>0,3например, х=2 и подставим вместо х в производную, получим: 10·2 -3= 17>0.Поставим справа от числа 0,3 знак плюс на числовой прямой.Там, где производная положительна (f ´(x) >0) функция возрастает, то есть возрастает напромежутке [ 0,3; +∞)
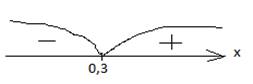Там, где производная отрицательна
(f ´(x)<0) функция убывает, то есть убывает на ( -∞; 0,3].
Пример2. Исследовать функцию f(x) = 3x2 –2x3+12хнавозрстание и убывание. Найти длину участка возрастания.
1.Область определения функции D(f) = R.
2. f ´(x) = (3x2 -2x3 +12х)´= 6х – 6х2 +12
3. f ´(x) = 0 6х – 6х2 +12 =0 разделим на 6 и перепишем по порядку. - х2 +х +2 = 0 Решим это квадратное уравнение, найдем дискриминант и корни.
D= 12 - 4·(-1)·2 = 1 + 8 = 9>0 - два корня. X1= ( - 1+√9)/ ( -2) =2/ (-2)= - 1;X2= ( - 1-√9)/ ( -2) =2
Отметим найденные точки на числовой прямой. Числовая прямая разбилась на три промежутка:
(-∞; -1] , [-1; 2] и [2; +∞). Прверим знак производной в каждом промежутке. На (-∞; -1] выберем, например, х = -3 и подставим в производную. . f ´(-3)= - ( -3)2 +(-3) +2= -9 -3 +2 = -10<0
В случае, когда производная получилась в виде квадратичной функции, то знак в каждом промежутке проверять не надо, достаточно определить знак в одном промежутке, в остальных знаки будут обязательно чередоваться. Изобразим числовую прямую и расставим знаки производной.
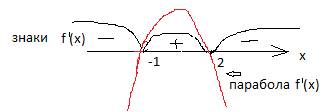
Производная положительна на [-1; 2] , значит на этом промежутке функция возрастает. Производная отрицательна на промежутках (-∞; - 1] и [2; +∞), значит функция убывает на этих промежутках. Найдем длину участка возрастания 2 – (-1) = 2 +1 =3.Ответ: функция возрастает на промежутке[-1; 2] , убывает на промежутках (-∞; - 1] и [2; +∞). Длина участка 3.
Примечание. Данные темы используются при решении заданий
№14 (базовый уровень), №7 (профильный уровень).
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
