"Производная. Применение производной" ч.2. 11 класс. Повторение.

Повторение. «Производная. Применение производной к исследованию функции».

11 класс. Часть 2.

Формулы производных и правила дифференцирования.

Тема 4.       Применение производной.

Нахождение экстремумов ( максимумов и минимумов) функции.

Краткая теория. (Разобрать, записать в тетрадь основные понятия, ответить на вопросы по теоретической части).

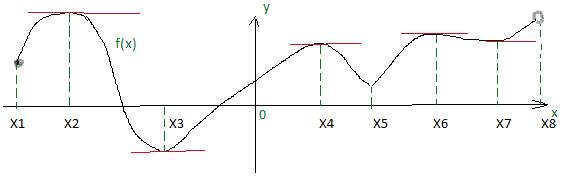
 Рисунок 1.  Рассмотрим внутренние точки области определения функции, изображенной на рис.1, в которых производная равна нулю или не существует. В точках, где производная равна 0, касательная параллельна оси ОХ. Это точки Х₂, Х₃, Х₄, Х₆ и Х₇.  В точке Х₅ касательную провести нельзя, т.к. острый график, поэтому в этой точке производная не существует.  На концах промежутка в точках Х₁ и Х₈ тоже касательные провести нельзя, так как нужна окрестность точки. На концах промежутка экстремумов не бывает.

Определение.  Точки, в которых производная функции равна 0 или не существует называются критическими.

На нашем  рисунке это точки Х₂, Х₃, Х₄, Х_5, Х₆ и Х₇.  Среди этих точек могут быть точки максимума ( max )и  минимума( min ), которые называются точкамиэкстремума       ( X_maxи X_min ). Значения функции в этих точках называют экстремумами функции   и обозначают f_max (X_max)  и  f_min (X_min).

Необходимым условием существования экстремумов является равенство нулю производной или если производная не существует, то есть необходимое условие – это наличие критических точек. (Это теорема Ферма), но этого условия еще не достаточно. Чтобы функция имела экстремум в некоторой точке, надо, чтобы при переходе через эту точку производная меняла свой знак, то есть надо, чтобы возрастание менялось на убывание, или убывание на возрастание. Если такой смены нет, то в этой критической точке не будет экстремума.

Если знак производной меняется с  (+ ) на (- ) – это точка max, если знак производной меняется с  (- ) на (+ ) – это точкаmin.

На рис.1:  Точка Х₂ является точкой max, т.к. при переходе через эту точку возрастание сменилось убыванием ( f´(x) поменяла знак с  (+ ) на (- )). Такими же будут точки  Х₄и Х_6.             В точках Х₃и Х₅ при переходе  f´(x) поменяла знак с  (- ) на (+ ). Это точки min.

В  критической точке Х₇ не произошло смены знака производной ( функция возрастала до этой точке и после нее). Здесь никакого экстремума нет. Это просто точка перегиба. Не будет существовать экстремумов и в точках, в которых график функции будут разрываться. На нашем рисунке такого случая нет.

Вывод. Для существования экстремумов необходимо выполнение двух условий:

1.      Существование критический точек.

2.      Смена знака производной при переходе через критическую точку.

Нахождение экстремумов функции осуществляют по следующему плану:

1.      Найти область определения функции.

2.      Найти производную.

3.      Найти критические точки ( приравнять производную к нулю).

4.      На числовой прямой отметить найденные критические точки, выделить            полученные числовые промежутки и проверить знак производной в каждом из них.

5.      Записать, где получились точки максимума или минимума, (а может быть и перегиба, если знак производной не менялся при переходе через точку, или разрыва).

6.      Вычислить значение  экстремумов функции (значение самой функции в точках экстремума.

7.      Для наглядности или когда надо построить график заданной функции, занести все полученные данные в таблицу.

Рассмотрим примеры.

Пример 1. Найти критические точки функцииf(x) =x³ -7x² -5x +6 (в ответ записать большее значение).Решение.

(В данном примере надо выполнить только три первых пункта плана.)

1.      D( f )= (- ∞; + ∞).

2.      Найдем производную f ´(x) =(x³ -7x² -5x +6)´ =3х² – 14х -5

3.      3х² – 14х -5=0      D= (-14)² - 4·3·(-5) = 196 + 60 = 256 = 16²

X₁ = (14+16)/(2·3) = 5      X₂ = (14 - 16)/(2·3) = - 1/3     Ответ: 5

Пример 2.Исследовать функциюf(x) =2x³ - 24x на экстремумы ( сделать таблицу, в ответ записать а) точку минимума; б) максимум функции).

Решение.

(В этом задании надо выполнить все пункты плана.)

1.      D( f )= (- ∞; + ∞).

2.      Найдем производную f ´(x) =(2x³ - 24x)´= 6х² – 24

3.      6х² – 24=0Здесь неполное квадратное уравнение, вынесем за скобки общий множитель  6 (х² – 4)=0;    х² – 4=0;     х² = 4;     х₁ =2 и х₂= - 2  это критические точки.  4. Знаки в промежутках определяют,  выбирая любые числа из каждого промежутка и подставляя в производную. Например, из промежутка ( -∞; -2) можно взять число         х= - 3.        6· (-3)² -24 = 6· 9 -24=30 > 0  (если квадратичная функция, знаки чередуются).          Пункт 5 .   Xmax = -2     Xmin = 2

6. f_max(-2) =2·(-2)³ - 24·(-2)=32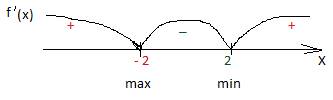

f_min(2) =2·(2)³ - 24·(2)= - 32

7.

Ответ:   а)  2               б)  32.

Пример 3.Исследовать функциюf(x) = Х+(1/х)на экстремумы ( сделать таблицу, в ответ записать  а) критические точки; б)  точку максимума; в) минимум функции).

Решение.

(В этом задании надо выполнить все пункты плана.)

1.      D(f ) = (- ∞; 0)  U (0; + ∞).      ( так как 1/х,    х≠0)

2.      Найдем производную f ´(x) =(Х +(1/х))´=1- (1/х²) = (х² -1) / х²

3.       (х² -1) = 0     х² =1      x₁ = -1   x₂ =1  при х=0 производная не существует.Критических точек 3. Это  -1; 0; 1.  Пункт 4.

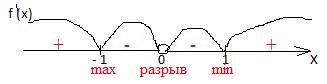Здесь функция не квадратичная функция и знаки надо проверять в каждом  промежутке.  Например, из промежутке   ( -1; 0) можно взять х= - 0,5.    1 - (1 / х²) = 1 – (1 /( - 0,5)²) = 1 –( 1/0,25)=  1 – 16 =-15 <0 ( поставили на рисунке знак минус.). Так проверяем знак в каждом промежутке в этом задании.

5.В этом примере две точки экстремума   Xmax = -1Xmin = 1

6. f_max(-1) =-1 +(1/-1)= -2

f_min(1) =1 +(1/1) = 2

7.

Ответ:  а)  -1;  0;  1.          б)  - 1.         в)  2.

Пример 4. Найти точку минимума функции   f(x) =e ^x+1 ·x⁵

1.  D( f )= (- ∞; + ∞).

 2.  Найдем производную f ´(x) =( e ^x+1 ·x⁵)´ =( e ^x+1) ´ ·x⁵+  e ^x+1 ·(x⁵)´= e ^x+1 ·x⁵+ e ^x+1 ·5x⁴  = e ^x+1 ·x⁴(x+5).     3.  e ^x+1 ·x⁴(x+5) =0, e ^x+1 ≠0 (показательная функция), x⁴ =0  х=0,  х+5=0      х= -5.  Это критические точки. Отметим найденные точки на числовой прямой и проверим знак производной в каждом из трех получившихся промежутков.

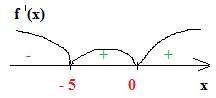
f ´(-6) = e ^-6+1 ·(-6)⁴(-6+5);   e ^-5   >0 ,(-6)⁴ >0, -1 <0 , f ´(-6) <0.

f ´(-1) = e ^-1+1 ·(-1)⁴(-1+5); e ⁰ =1 >0, ,(-1)⁴ >0,   4>0,  f ´(-1) >0.

f ´(1) = e ¹⁺¹ ·(1)⁴(1+5); e ²  >0, ,(1)⁴ >0,   6>0,  f ´(1) >0

В точке х = - 5 производная f ´(x) меняет знак с (-) на (+) ,точка х = - 5 – точка минимума. В точке х=0 производная не меняет свой знак – это точка перегиба.  Х_min = -5         Ответ: -5.

Применение производной.

Тема № 5. Исследование функции по графику ее производной.

В предыдущих заданиях осуществлялось исследование функции по ее графику. В этих примерах задавался график функции, на котором было видно, где функция возрастает, где убывает, где у нее  максимумы или минимумы. Если  задается график не самой функции, а ее производной, то в таких примерах для ответа на вопросы, надо применить изученную теорию. (Повторите темы №3 и №4:«Исследование функции на монотонность» и «Исследование на экстремумы»).

Пример. Задан график производной некоторой функции. По графику ответить на вопросы.(цветных линий на исходном графике нет, проведены позже). 

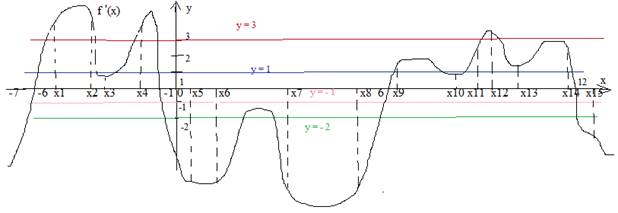
Вопросы.

1.      Количество промежутков возрастания функции.Пояснение: Функция возрастает там, где производная положительна, т.е. это те участки графика производной, которые лежат выше оси х. Это промежутки [ -6; -1] и [ 6 ;12].

Ответ:  2

2.      Длина н наибольшего участка возрастания. 

Посчитаем длину первого второго промежутки и выберем наибольшую длину.

-1 –(-6) = -1 + 6 =5               12 – 6 = 6         

Ответ:  6  

3.      Длина  наименьшего участка возрастания.      Ответ:   5  

4.      Количество промежутков убывания.

Функция убывает там, где производная отрицательна, т.е. это те  участки графика производной, которые лежат ниже оси х. Это промежутки ( - ∞; -6] ,[ -1 ; 6 ] и [12; + ∞]

Ответ:  3  

5.      Длина  наименьшего участка убывания.

Наименьший участок по длине [ -1 ; 6 ], т.к. длины, содержащие бесконечность вычислить нельзя. Его длина  6 – ( -1) = 6 +1 = 7.          Ответ:  7  

6.       Сколько точек Х₁…Х₁₅, в которых функция возрастает.

Надо подсчитать, сколько точек попадает на участки возрастания, то есть на те участки графика производной, где производная f  ´(x) > 0, участкикоторые располагаются выше оси ОХ.  Это точки Х₁,Х_2,Х₃ Х₄, Х₉,  Х₁₀, Х₁₁, Х₁₂, Х₁₃Х_14.Ответ:  10

7.      Сколько точек Х₁…Х_15,  в которых   функция убывает.

Надо подсчитать, сколько точек попадает на участки убывания, то есть на те  участки графика производной, где производная  f  ´(x) <0, участки которые располагаются ниже оси ОХ.  Это точки Х₅,Х₅,  Х₇, Х₈, Х_15.Ответ:  5

8.      Сколько точек, где касательная к графику функции (не к графику производной) параллельна оси ОХ.

По условию касательная параллельна оси ОХ, значит, производная в этих точках равна нулю f  ´(x) =0. На графике функции это точки экстремума, а на графике производной, который у нас задан, это точки пересечения с осью ОХ.Надо подсчитать, сколько  таких точек. Это точки Х= - 6, Х= -1, Х=6, Х=12.

Ответ:  4

9.      Сколько точек, где угол наклона касательной к графику функции равен 45°.

Производная связана с углом наклона касательной к графику функции соотношением: f  ´(x₀) = tgaЕсли угол наклона касательной равен 45°, tg45°=1

f  ´(x₀) =1. Проведем на графике прямую y =1 ( дополнительная  синяя прямая)

и подсчитаем, сколько получилось точек пересечения с нашим графиком.

Ответ:  8

10.  Сколько точек, где угол наклона касательной к графику функции равен 135°.

Если угол наклона касательной равен 135°, tg135°= -1

f  ´(x₀) =-1. Проведем на графике прямую y = -1 ( дополнительная  розовая прямая)и подсчитаем, сколько получилось точек пересечения с нашим графиком.Ответ:  4

11.  Сколько точек, где угловой коэффициент наклона касательной к графику функции равен 3.

Производная связана с угловым коэффициентом наклона касательной к графику функции соотношением: f  ´(x₀) = к  к – угловой коэффициент.

Уравнение любой прямой имеет вид:  у=кх + b.  Так как у нас к=3, то надо провести дополнительную прямую у=3 (коричневая прямая)и подсчитать, сколько получилось точек пересечения с нашим графиком.Ответ:  6

12.  Сколько точек, где касательная к графику функции (не к графику производной) параллельна прямой у = 5 – 2х.

Так как у нас к= -2, то надо провести дополнительную прямую у= -2 (зеленая прямая) и подсчитать, сколько получилось точек пересечения с нашим графиком.Ответ:  6

13.   а)Сколько точек, где касательная к графику функции (не к графику производной) параллельна прямым  у =  - 8 или у = - 0,5 или у =10.

б) найти сумму абсцисс этих точек.

а) Для всех этих прямых угловой коэффициент равен 0 (в уравнении касательной у=кх + b множитель, стоящий перед Х отсутствует, т.е. к =0). f  ´(x₀) = 0на графике функции это точки экстремума, а на графике производной, который у нас задан, это точки пересечения с осью ОХ.Надо подсчитать, сколько  таких точек. Это точки Х= - 6, Х= -1, Х=6, Х=12.  а)Ответ:   4

б) Подсчитаем сумму абсцисс этих точек   - 6+ (- 1)+6 +12 =11.

б)Ответ:   11

14.    Количество экстремумов функции.

В точках экстремума производная равна нулю и меняет знак при переходе через это точку. Х= - 6, Х= -1, Х=6, Х=12.

Ответ:  4

15.   а)  Количество точек максимума, б) Сумма абсцисс точек максимума.

Максимум функции бывает в тех точках, при переходе через которые производная меняет свой знак с плюса на минус. (т.е. до этой точки график находился выше оси ОХ, а после этой точки график лежит ниже оси ОХ.). В нашем примере это точки Х= -1 и  Х=12. В этих точках производная поменяла знак с (+) на ( - ).       а)Ответ:   2

б) Подсчитаем сумму абсцисс этих точек   - 1 + 12 = 11.    б)Ответ:   11

16. а)  Количество точек минимума, б) Сумма абсцисс точек минимума.

Минимум функции бывает в тех точках, при переходе через которые производная меняет свой знак с  минуса на плюс. (т.е. до этой точки график находился ниже оси ОХ, а после этой точки график лежит выше оси ОХ.). В нашем примере это точки Х= -6 и  Х=6. В этих точках производная поменяла знак с (-) на ( + ).       а)Ответ:   2

б) Подсчитаем сумму абсцисс этих точек   - 6 + 6 = 0.    б)Ответ:   0

17. Наименьшая точка максимума.

Точки  максимума Х= -1 и  Х=12. Наименьшая Х= -1.Ответ:   - 1

18.  Наибольшая точка минимума.

Точки  минимума Х= -6 и  Х=6. Наибольшая Х= 6.Ответ:   6

19.   В какой точке на промежутке [ -1;6 ] функция принимает свое  а) наибольшее значение, б) наименьшее значение.

а) На промежутке [ -1;6 ] график производной находится ниже оси ОХ. На этом промежутке производная отрицательна,  сама функция убывает и ее график пойдет вниз.  Наибольшее значение примет в т. Х= -1, наименьшее значение в т. Х= 6.         а)Ответ:   -1 б)Ответ:  6

20.   В какой точке на промежутке [ 6 ; 12 ] функция принимает свое  а) наибольшее значение, б) наименьшее значение.

а) На промежутке [ 6;12 ] график производной находится выше оси ОХ. На этом промежутке производная положительна,  сама функция возрастает и ее график пойдет вверх.  Наибольшее значение примет в т. Х=12, наименьшее значение в т. Х=6а)Ответ:  12б)Ответ:  6

Применение производной.

Тема № 6. Нахождение наибольшего и наименьшего значения функции на отрезке.

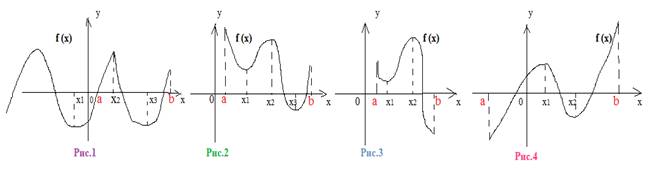
Краткая теоретическая часть(конспект вместе с разобранными примерами). Рассмотрим, как производная используется для нахождения  наибольшего  и наименьшего значения функции  на отрезке. Наибольшее и наименьшее значение непрерывной функции на отрезке может быть как на концах отрезка, так и внутри него. ( в отличие от  экстремумов функции, которые на концах промежутка не могут быть). Если наибольшее или наименьшее значение достигается внутри отрезка, то это только в стационарных точках (где производная равна нулю)  или в критических( где производная не существует).Будем их называть одним словом «Критические».Рассмотрим рисунки.

Рис.1.На отрезок[a;b]попадают две  критические точки (Х₂ и Х₃). В точке Х₂будет наибольшее значение, в точке Х₃ - наименьшее. В данном случае наибольшее значение совпало с максимумом функции, наименьшее значение совпало с минимумом функции.  У_наиб(Х₂)  и У_наим (Х₃)  .

Рис.2. На отрезок[a;b]попадают три  критические точки (Х_1, Х₂ и Х₃). Наибольшее значение получилось на конце промежутка в т.а : У_наиб(а) , наименьшее – в критической точке  Х₃ :

У_наим (Х₃) .

Рис.3.На отрезок[a;b]попадают две  критические точки (Х₁ и Х₂). В данном случае наибольшее значение совпало с максимумом функции в точке Х_{2 ::} У_наиб(Х₂),  наименьшее значениеполучилось на конце промежутка в т. b:У_наим (b).

Рис.4.На отрезок[a;b]попадают две  критические точки (Х₁ и Х₂). Наибольшее и наименьшее значение оказываются на концах отрезка:   У_наиб(b),  У_наим (а).

Алгоритм нахождения наибольшего и наименьшего значения функции  y=f(x) на отрезке [a;b]

1.       Найти производнуюf  ´(x).

2.       Найти стационарные и критические точки  (приравнять производную к нулю, то есть

найти  f  ´(x)=0).

3.        Из полученных точек выбрать те, которые попадают в заданный  по  условию отрезок.

4.       Вычислить значение функции в выбранных точках и на концах промежутка.

5.        Из полученных чисел выбрать самое наибольшее У_наиби самое наименьшееУ_наим.

Рассмотрим примеры на данную тему.

Пример 1. Найти наибольшее и наименьшее значение функции f(x)= х⁴ - 2x²– 3   на отрезке  [ 0; 2]. В ответ записать наименьшее значение.

Решение.

1.Найти производную f  ´(x).

f ´ (x)= (х⁴ - 2x² – 3 )´ = 4х³ - 4 х

2. Найти  f  ´(x)=0.

4 х³ - 4 х =0      4х ( х² – 1 )= 0    4 х= 0    х² – 1 =0     х = 0,  х= 1,  х= - 1

3.  Из полученных точек   х = 0,  х= 1,  х= - 1  выбрать те, которые попадают в заданный отрезок [ 0; 2].

0ϵ[ 0; 2],       1ϵ[ 0; 2],        - 1 не ϵ[ 0; 2].

4. Вычислим значение заданной функции в выбранных точках    х = 0,  х= 1 и на концах отрезка[ 0; 2].

f(0)= 0⁴– 2 · 0²– 3 = - 3

f(1)= 1⁴– 2 ·1²– 3  = -4

f(2)= 2⁴– 2 ·2²– 3  = 5

Пример 2. Найти наибольшее и наименьшее значение функции f(x)= х³/ 3 - x²/2–2х +10на отрезке  [ -3; 3]. В ответ записать наибольшее значение. (Ответ округлить до десятых).

Решение.

1.      f ´(x)= (х³/ 3 - x²/2–2х +10)´= х² – х -2

2.      х² – х -2 = 0     D = ( -1)² – 4 ·1· (- 2) = 1 +8 =9 = 3²

X₁ = ( 1+√9) / 2 = (1+3) / 2 =2           X₂ = ( 1- √9) / 2 = (1-3) / 2 = - 2 / 2  = - 1

3.       2ϵ[ -3; 3],      - 1ϵ[ - 3; 3].

4.      f(2)= 2³ / 3 - 2²/2–2 ·2 +10 = 8 / 3 -2 - 4 +10 = 6,7

 f(- 1)= (-1)³/ 3–(-1)²/2–2·(- 1) +10= (-1) / 3 – 1 / 2 +2 + 10 = 11,17

f(-3)= (-3)³/ 3–(-3)²/2–2(-3) +10= - 9 -4,5 + 6+ 10 =2,5

f(3)= 3³/ 3 - 3²/2–2·3 +10= 9 - 4,5 – 6 + 10 = 8,5

fнаиб(2)  =11,17fнаим (1)  = 2,5             Ответ:   11,2

Пример 3. Найти наибольшее и наименьшее значение функции f(x)= 9Cosx + 16x - 8на отрезке  [ -3π/2; 0]. В ответ записать наибольшее значение.

Решение.

1.    f´ (x)= (9 Cos x + 16x - 8 )´  = - 9 Sinx +16

2.    - 9 Sinx +16 =0      - 9 Sinx =- 16      Sinx = ( - 16) / (- 9)= 1,8  > 1 – нет решения, так как     - 1 <Sinx< 1.  Критических точек нет. Сразу выполняем пункт 4.

3.    Найдем значение функции на концах промежутка.

f(-3π/2)= 9 Cos(-3π/2)+ 16 ·(-3π/2) - 8 = 9Cos(π/2) - 24π -8 =

9 ·0 - 24·3,14 – 8= - 83,36

f( 0)= 9 Cos (0 )+ 16 ·( 0) - 8 = 9·1 + 0– 8 =1

fнаиб(0)  =1fнаим (-3π/2)  =- 83,36            Ответ:   1

Пример 4. Найти наибольшее и наименьшее значение функции f(x)= 12 tgx– 12x+ 3π - 13на отрезке  [ -π/4; π/4]. В ответ записать наибольшее значение.

Решение.

1.      f ´(x)= (12 tg x – 12x+ 3π – 13)´  = 12 / Cos² x – 12 + 0 – 0

(Примечание: производная(3π)´ = 0 так как это постоянная величина)

2.      12 / Cos² x – 12 =0  12(1/ Cos² x – 1)=0       1/ Cos² x =1

Cos² x =1  Cosx =1 иCosx = - 1. Получили два  простейших тригонометрических уравнения, для которых используем формулы частных случаев.

Cosx =1  х = 2πn,  nϵZ.   При  n = 0х = 2π·0 =0

Cosx = - 1х =π + 2πn,  nϵZ.   При  n = 0х = π + 2π·0 =π

3.      0 ϵ[ -π/4; π/4],πнеϵ [ -π/4; π/4].

4.      f(0)= 12 tg0– 12·0+ 3π - 13=12·0 - 12·0 +3·3,14 -13= -3,6

f(-π/4)= 12 tg(-π/4) – 12·(-π/4) +3π - 13 =12·( -1) + 3π +3π – 13=

-12 +6π -13 = -25 +6π = -25 +18,84 = - 6,16

f(π/4)= 12 tg(π/4) – 12·(π/4) +3π - 13 =12·( 1) - 3π +3π – 13= - 1

fнаиб(π/4)  = -1fнаим (-π/4)  =- 6,16           Ответ:         - 1

Пример 5. Найти наименьшее значение функции f(x)= 7x - 7 ln(x+5)+3,8 на отрезке  [ -4,9; 0].

Решение.

  1. f´ (x)= (7x - 7 ln(x+5)+3,8 )´ = 7 - 

  2. 7 -= 0; ;  x+5 ≠0;x≠ -5; 7x+28=0; x= - 4.

   - 4 ϵ[ -4,9; 0].

f( - 4)=7·(-4) - 7· ln(-4+5)+3,8 = -28 -7· ln 1 +3,8 =-28 -7·0 +3,8= - 24,2

-34,3 - 7·0,6 +3,8

f(-4,9)=7·(-4,9) - 7· ln(-4,9+5)+3,8 =-34,3 - 7·ln0,1 +3,8= -34,3 - 7·(-2,3) +3,8 =

-34,3+16,1+3,8=-14,4

-34,3 - 7·0,6 +3,8

Задания №14 базовый уровень. Задание №12 профильный уровень.