Проценты в нашей жизни

Государственное учреждение образования

 «Суйковскаябазовая  школа Витебского района»

Школьная научно-практическая конференция

математика

Проценты в нашей жизни

Работу выполнил:

Макаров Сергей, ученик 6 класса

Руководитель:

Волкова Татьяна Васильевна,

учитель математики

Суйково, 2021

Содержание

   1.Введение ………………………………………………………….3-4

   2. Основная часть……………………………………………………5-12

2.1.          Из истории происхождения процентов………………………4-5

2.2.          Проценты в повседневной жизни…………………………….5

2.3.          Проценты в медицине………………………………………….6

2.4.          Проценты в кулинарии…………………………………………6

2.5.          Проценты в бухгалтерии……………………………………….6

2.6.          Интересные факты в процентах………………………………7

2.7.          Проценты в нашей школе……………………………………...8

3.        Решение задач на проценты разными способами……………….8-10

4.        Заключение……………………………………………………….10

5.        Список литературы………………………………………………11

6.        Приложения………………………………………………………12-15

В математике есть термин, 
Именуется  «процент».
Я вам с точностью отвечу:
Проще ничего и нет.
Это, кто ещё не знает,
Одна сотая числа.
Кто процент легко считает, 
Тот повсюду голова.
Измеряются в них скидки,
Что торговцы нам дают,
Вклады в банках и кредиты,
И инфляция валют.

1.     Введение

В 6 классе мы изучили тему «Проценты». Мне эта тема показалась тесно связанной с реальной жизнью. Очень часто, приобретая ту или иную вещь, мы подсчитываем свои доходы и расходы. Я увидел связь между темой «Проценты» и экономической стороной жизни.

Проценты - это одна из сложнейших тем математики, и очень многие учащиеся затрудняются или вообще не умеют решать задачи на проценты.  А понимание процентов и умение производить процентные расчёты необходимы для каждого человека. Прикладное значение этой темы очень велико и затрагивает финансовую, экономическую, демографическую и другие сферы нашей жизни. Изучение процента продиктовано самой жизнью. Умение выполнять процентные вычисления и расчеты необходимо каждому человеку, так как мы ежедневно встречаемся с ценами на товары и услуги, приходится иметь дело при оформлении в банке сберегательного вклада или кредита, покупке товара в рассрочку, при выплате налогов, страхования.

Актуальность выбранной темы заключается в необходимости решения практических задач на уроках математики и применении их в жизни, т.к. они имеют социальную значимость, помогают разобраться в новых экономических веяниях жизни.

Гипотеза проекта:

Тема "Проценты" имеет практическое применение.

 Цели исследовательской работы:

·         Расширение знаний о применении процентных вычислений в задачах и из разных сфер жизни человека.

·        Составить и решить задачи по данной тематике.

Задачи:

1.     Изучить научную литературу по теме исследования.

2.     Показать применение понятия процента при решении задач.

3.     Показать использование процентов в своей школе.

4.     Провести статистическое исследование и представить данные в виде диаграмм.

5.     Обобщить результаты работы.

Методы исследования:

1. Изучение литературы по данной теме.

2. Получение экономических знаний для расчётов, изучение теоретического материала.

3. Решение задач.

                                                                                                                                        2.            Основная часть

2.1. Из истории происхождения процентов

Проценты – одно из математических понятий, которые часто встречаются в повседневной жизни. Так, мы часто читаем или слышим, что например, в выборах приняли участи 52,5% избирателей, рейтинг победителя хит-парада равен 75%, уровень инфляции 8% в год, банк начисляет 12% годовых, молоко содержит 3,2% жира, материал содержит 60% хлопка и т.д.

Слово «процент» происходит от латинского procentum, чтобуквально означает «за сотню» или «со ста». Процентами очень удобно пользоваться на практике, так как они выражают целые части чисел в одних и тех же сотых долях. Знак «%» происходит, как полагают, от итальянского слова cento(сто),которое в процентных расчетах часто писалось сокращенно cto. Существует и другая версия возникновения этого знака. Предполагается, что этот знак произошел в результате нелепой опечатки, совершенной наборщиком. В 1685 году в Париже была опубликована книга «Руководство по коммерческой арифметике» Матье де ла Порта. В одном месте речь шла о процентах, которые тогда обозначали «cto» (сокращённо от cento). Однако наборщик принял это «cto» за дробь и напечатал «%». Так из-за опечатки этот знак вошёл в обиход.

Впервые опубликовал таблицы для расчета процентов в 1584 году Симон Стевин - инженер из города Брюгге (Нидерланды). Стевин известен замечательным разнообразием научных открытий в том числе – особой записи десятичных дробей.

Проценты применялись только в торговых и денежных сделках. Затем область их применения расширилась, проценты встречаются в хозяйственных и финансовых расчетах, статистике, науке и технике. Ныне процент - это частный вид десятичных дробей, сотая доля целого (принимаемого за единицу).

В популярной литературе возникновение этого термина связывается с внедрением в Европе десятичной системы счисления в XV веке.

Основные области применения процентов

2.2.          Проценты в повседневной жизни

В повседневной жизни люди сталкиваются с процентами ежедневно.

При посещении магазинов мы видим яркие объявления о скидках и распродажах. Выгода распродаж для покупателей очевидна – это возможность приобрести качественный товар по сниженным ценам.

В последние годы в средствах массовой информации довольно часто можно услышать о повышении тарифов на коммунальные услуги, чаще все цифры озвучиваются в процентах. Кредиты в банковской сфере выдаются людям под процент.

Также очень многие люди в целях безопасности и увеличения суммы денег хранят  свои денежные средства в банках под процентами.

На выборах победа партии или кандидата так же определяется в процентах.

2.3.          Проценты в медицине и фармацевтике

Медицинские работники ежедневно сталкиваются с умением рассчитать проценты. Одна из основных задач фармакологии – разработка лекарственных препаратов, помогающих в борьбе с тем или иным заболеванием.

Фармацевты, опытным путем, используя теоретическое знание, составляют растворы лекарственных веществ в таких пропорциях, чтобы оказать помощь организму человека, и в то же время не нанести вред.

Покупая любое лекарство больной перед его использованием внимательно изучает инструкцию к нему, в которой подробно перечислен состав препарата с указанием процентного содержания всех входящих в него веществ.

2.4.Проценты в кулинарии

Уксус - одна из самых древних приправ, которая используется в приготовлении множества кулинарных рецептов, а также для консервации продуктов на зиму. Вот только разнообразие блюд требует различного процентного содержания уксуса. В некоторые блюда рецептура требует наличия уксуса 70%, в то время как в другие достаточно добавить 6 или 9-процентный уксус.

А так как под рукой не всегда можно найти уксус нужного процентного содержания, то приходится самостоятельно производить расчет количества воды, который необходимо добавить в уксусную кислоту, чтобы получить уксус с необходимым процентом кислоты

2.5.Проценты в бухгалтерии

Бухгалтер ежемесячно, начисляет заработную плату всем сотрудникам предприятия, производит отчисления в налоговую инспекцию, пенсионный фонд, в фонд социального страхования и прочие. Все отчисления рассчитываются индивидуально для каждого сотрудника, но при этом бухгалтер пользуется единой для всех процентной ставкой.

2.6.Интересные факты в процентах

Умение вычислять проценты очень важно при приготовлении сплавов, например, для получения сплава золота 585 пробы необходимо 58.5% чистого золота и два основных лигатурных металла: медь (33.5%) и серебро (8%). Из-за достаточно большого количества золота, внешний вид изделия из 585 пробы не тускнеет в процессе эксплуатации.

Все живые животные и растительные существа состоят из воды: животные – на 75%,  рыбы – на 75%,  медузы – на 99%,  картофель - на 76%, помидоры - на 90%, огурцы - на 95%, яблоки - на 85%, арбузы - на 96%. Даже человек состоит из воды. 86% воды содержится в теле у новорожденного и до 50% у пожилых людей.

Если человек теряет 2% воды от массы своего тела, то у него возникает сильная жажда. Если проценты потерянной воды увеличатся до 10, то у человека начнутся галлюцинации. При потере в 12% человек не сможет восстановиться без помощи врача. При потере в 20% человек умирает.

Вода не только дарит жизнь, но может и отнимать ее, 85% всех заболеваний в мире передается с помощью воды.

Страна - крупнейший производитель кислорода в мире – Россия. В Сибири растёт примерно 25% мировых лесов, это делает Россию самым мощным в мире переработчиком углекислого газа в ценнейший кислород.

Проценты также активно применяются в картографии.

Например, площадь нашей Витебской  областисоставляет40 000 км², что составляет около 20% территории всей республики Беларусь. А численность населения Витебской  области1 187 000 чел (2018г), что составляет 12% населения РБ.

2.7. Проценты в нашей школе

Всю нашу школу можно представить в виде процентов.

Всего учащихся 65 человек, из них 29 (45%) девочек и 36 (55%) мальчиков.

Рассмотрим данные показатели в процентом соотношении от общего количества учащихся школы и построим диаграмму.

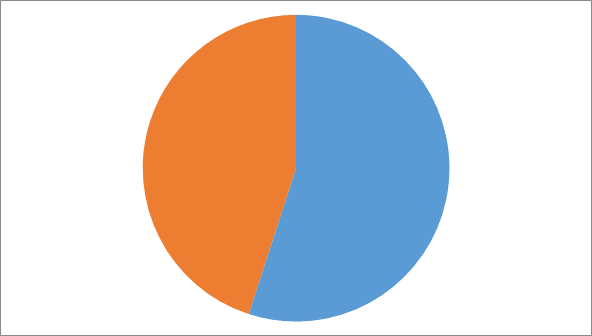
В нашем 6 классе 5 учащихся, это составляет 7,7 % от общего количества учащихся школы. Из них – 2 девочки в классе (40% от общего количества класса), 3 мальчика –(60%от общего количества класса).

3.Решение задач на проценты разными способами

При решении задач на проценты мыприменяли следующие правила:

1)    Нахождение процентов от числа: Чтобы найти проценты от числа нужно, проценты превратить в десятичную дробь и число умножить на эту дробь.

2)    Нахождение числа по его процентам: Чтобы найти число по его процентам нужно, проценты превратить в десятичную дробь и число разделить на эту дробь.

3)    Нахождение процентного отношения чисел: Чтобы найти процентное отношение чисел, надо отношение этих чисел умножить на 100.

Задачи с процентами можно решить разными способами:

1)    уравнением;

2)    составлением таблицы;

3)    применяя пропорцию;

4)    по действиям, используя правила.

Рассмотрим простые задачи на проценты:

1)                Определение процента от числа.  Найти: 25% от 120.                                   Решение: 1) 25% = 0,25; 2) 120 . 0,25 = 30. Ответ:30.

2)                Определение числа по известной его части, выраженной в процентах

Найти число, если 15% его равны 30.                                                                                 Решение: 1) 15% = 0,15; 2) 30 : 0,15 = 200.    или:  х - данное число;  0,15.х = 300;  х = 200.      Ответ: 200.

После рассмотрения этих простейших задач можно рассмотреть задачи типа:

1)    На сколько процентов 10 больше 6?    ((10 - 6).100%)/6 = 66 2/3 (%)     

2)     На сколько процентов 6 меньше 10?   ((10 - 6).100%)/10 = 40(%)

3)    Что произойдет с ценой товара, если сначала ее повысить на 25%, а потом понизить на 25%?   

Решение: Пусть цена товара х руб.                                                                                         1) х + 0,25х = 1,25х;

2) 1,25х - 0,25.1,25х = 0,9375х;                                                                                                            3)  х - 0,9375х = 0,0625х;  4) 0,0625х/х . 100% = 6,25%.                                                              Ответ: первоначальная цена товара снизилась на 6,25%.

4)                 Свежие грибы содержали по массе 90% воды, а сухие 12%.                              Сколько получится сухих грибов из 22 кг свежих?                                              Решение:1) 22 . 0,1 = 2,2 (кг) - грибов по массе в свежих грибах;                                                      2) 2,2 : 0,88 = 2,5 (кг) - сухих грибов, получаемых из свежих.                                 Ответ: 2,5 кг.

При решении задач на проценты приходится сталкиваться с понятием "процентное содержание", "концентрация", "%-й раствор". Такие  задачи на проценты будут встречаться на уроках химии.

1) Сколько кг соли в 10 кг соленой воды, если процентное содержание соли 15%.                                                                                                                                           2) Сплав содержит 10 кг олова и 15 кг цинка. Каково процентное содержание олова и цинка в сплаве?                                                                                         

 3)  Концентрация серебра в сплаве 300 г составляет 87%.  Сколько чистого серебра  в  сплаве?

Выводы:

Задачи на проценты имеют большое практическое значение и приобретенные знания, я надеюсь, помогут мне в дальнейшей жизни.    Я планирую развивать начатую тему, простые и сложные проценты, решать различные виды задач на проценты. Чтобы быть современным человеком, необходимо иметь возможность самому вычислять возможные выплаты по кредиту или хотя бы примерно знать, стоит ли брать кредит или ссуду.

4.Заключение

Роль процентов в жизни человека велика. Трудно назвать область, где бы ни применялись проценты. С помощью процентов более ярко можно донести нужную информацию до любого человека. Умение выполнять процентные вычисления и расчеты необходимо каждому человеку, так как с процентами мы сталкиваемся в повседневной жизни. Проценты дают возможность легко сравнивать между собой части целого, упрощают расчёты и поэтому очень распространены. Поэтому нужно хорошо знать и уметь с легкостью пользоваться этой темой.

В ходе работы над данным проектом я пришел к выводу, что проценты помогают нам:

·                     грамотно разбираться в большом потоке информации;

·                     совершать выгодные покупки, экономя со скидками;

·                     решать математические задачи.

Хорошо ориентируясь в мире процентов, мы понимаем, что выгодно брать кредит в том банке, где процент меньше; а товар выгоднее покупать тот, на который больше скидка. Таким образом, знания помогают современному человеку следить за своими расходами и повышать уровень благосостояния.

Получившаяся в результате работы примеры решения задач позволят мне с легкостью освежить знания по теме «Проценты» перед любым серьезным экзаменом и контрольной работой. Надеюсь, и Вы найдете ей применение.

5.Список использованных источников

1.                 Виленкин Н.Я., За страницами учебника математики / Н.Я. Виленкин, И.Я. Депмана. – М.: Просвещение, 1989г.

2.                 Виленкин Н.Я., Математика. 5 класс: учеб. для учащихся общеобразовательных учреждений /Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – М.: Мнемозина, 2013г.

3.                 История процентов. Такая разная математика [Электронный ресурс] -https://rasnajamatematika.blogspot.ru/2013/05/blog-post.html

4.                 Что такое процент [Электронный ресурс] - https://www.kakprosto.ru/kak-80088-chto-takoe-procent#ixzz59d6QozMK

5.                 Шурыгин В. А., Кочергина Т. И. Три основных действия с процентами. Математика вокруг нас // Юный ученый. - 2015. - №2. - с. 94-95.

6.     Приложения

Расчетные задачи по теме "Проценты".

1.   Найти 14% от 84.

2.   Найти число, если 12% его составляют 9,03.

3.   Цена товара 64 руб. После снижения цен товар стал стоить 57 руб. На сколько процентов снижена цена?

4.   При продаже товара за 1548 руб. получено 20% прибыли. Определить себестоимость товара.

5.   Свежие фрукты содержали 72%, а сухие - 20%. Сколько сухих фруктов получится из 20 кг свежих?

6.   Кусок сплава меди и олова весом 12 кг содержит 45% меди. Сколько олова надо добавить к этому куску, чтобы в новом сплаве было 40% меди?

7.   Имеется лом стали двух сортов с содержанием никеля в 5% и 40%. Сколько нужно взять каждого из этих сортов, чтобы получить 140 т стали с содержанием никеля в 30%?

8.   Сколько чистого спирта надо добавить к 735 г 16%-ного раствора йода в спирте, чтобы получить 10%-ный раствор?

9.   Сбербанк начисляет по вкладам ежегодно 110%. Вкладчик внес в сбербанк 150 тыс. руб. Какой будет сумма вклада через 2 года?

10.Площадь прямоугольника равна 100 см2. Одна сторона прямоугольника уменьшилась на 16,4%, вторая увеличилась на 25%. Найти площадь нового прямоугольника.

11.  Предприниматель «Некто» продал вещь за 9 рублей, потеряв при продаже столько процентов, сколько рублей стоила эта вещь первоначально. Сколько рублей стоила вещь первоначально?

12. Магазин продал книгу со скидкой в 10% по сравнению с первоначально назначенной ценой и получил при этом 8% прибыли. Сколько процентов прибыли первоначально предполагал получить магазин?

Задачи на сплавы

1.   Имеется 2 сплава, в одном из которых содержится 40%, а в другом 20% серебра. Cколько кг второго сплава нужно добавить к 20 кг первого, чтобы после сплавления вместе получить сплав, содержащий 32% серебра?

2.   Имеется 2 сплава, в одном из которых содержится 20%, а в другом 30% олова. Сколько нужно взять первого и второго сплавов, чтобы после их сплавления вместе получить 10 кг нового сплава, содержащего 27% олова?

3.   Имеется 2 сплава, в одном из которых содержится 10%, а в другом 20% меди. Сколько нужно взять первого и второго сплавов, чтобы после их сплавления вместе получить 15 кг нового сплава, содержащего 14% меди?

4.   Имеется 2 сплава, в одном из которых содержится 30%, а в другом 50% золота. Cколько кг второго сплава нужно добавить к 10 кг первого, чтобы после сплавления вместе получить сплав, содержащий 42% серебра?

5.   Сплав золота и серебра содержит 20% золота. Какую массу сплава и какую массу чистого золота нужно взять для получения 80 кг нового сплава, содержащего 50% золота?

6.   Кусок железа с медью массой в 30 кг содержит 45% железа. Какую массу меди нужно добавить к этому куску, чтобы полученный новый сплав содержал 30% железа.

7.   Сплав олова и свинца содержит 40% олова. Какую массу сплава и какую массу чистого свинца нужно взять для получения 40 кг нового сплава, содержащего 10% олова?

Хитрые задачки

1.Число увеличили на 10%, потом ещё на 10%. На сколько процентов увеличили число за два раза?

Решение: Пусть число было равно m . Сначала его увеличили на 10% , т. е. на 0,10m . Получили m+0,10m=1,10m. Теперь полученное число увеличим на 10%, умножив его на 1,10: 1,10х(1,10m)=1,21m.

Ответ: последний результат на 21% больше данного числа.

2.Хранили 20 кг крыжовника, ягоды которого содержат 99% воды. Содержание воды в ягодах уменьшилось до 98%. Сколько крыжовника получилось в результате?

Решение: На первый взгляд, кажется, что вес ягод мало изменился, но это только на первый взгляд! Вес сухого "вещества" в ягодах составлял 100-99=1(%), или 20х0,01=0,2(кг). После сушки его вес составляет 100-98=2(%) от нового веса ягод. Найдём новый вес ягод: 0,2:0,02=10(кг).

Ответ: после сушки вес ягод уменьшился в два раза!

Интересные задачи.

1. Скорость Мартышки на 100% больше скорости Слоненка. Скорость Слоненка 15км/ч. Какова скорость Мартышки?

2. Мартышка собиралась съесть за неделю 30 бананов, но съела на 20% больше. Сколько бананов съела Мартышка?

3. Попугай подлетел к Удаву и сообщил: «Ура! Цена на шоколад понизилась на 10%. Сколько теперь будет стоить 10-рублевая шоколадка?

4. Число увеличили на 10%,потом уменьшили на 10%. Увеличилось или уменьшилось число за два раза? На сколько процентов?

5. Слонёнок за весну похудел на 20%, потом поправился за лето на 30%, за осень опять похудел на 20% и за зиму прибавил в весе на 10%. Остался ли за этот год его вес прежним? Если изменился, то на сколько и в какую сторону?

Анекдот

Пожилая учительница встречает на улице своего бывшего выпускника.

- Володя я очень рада тебя видеть. Как ты сейчас живешь?

- Все у меня о-кей, Марьванна. Бизнесом занимаюсь, торгую.

-Да как же это ты бизнесом-то занимаешься? Ты ведь в школе даже проценты усвоить не мог!

- А че, там усваивать? Вот покупаю коробку американских сигарет за 17 долларов, а продаю – за 19. На эти два процента и живу.

Скачано с www.znanio.ru