Proyeksiyalar tekisliklarini ketma-ket ikki marta almashtirish

Proyeksiyalar tekisliklarini ketma-ket ikki marta almashtirish.

Ayrim geometrik masalalarni yechishda proyeksiyalar tekisliklarini ketma-ket ikki marta almashtirish zarur bo‘ladi.

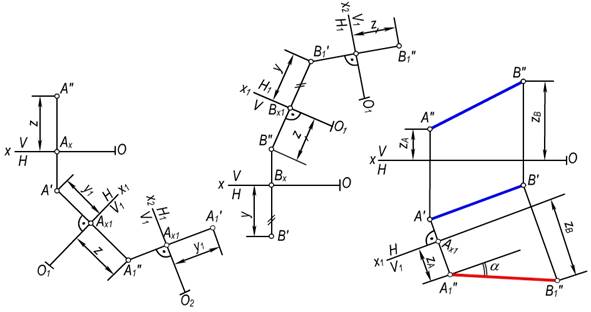
166–rasmda A nuqtaning  tizimida berilgan A′ va A″ proyeksiyalari orqali uning yangi A′₁ va A″₁ proyeksiyalarini yasash ko‘rsatilgan. Buning uchun avval V tekislikni V₁ tekislik bilan almashtirib,  tizimi hosil qilinadi. Buning uchun chizmada ixtiyoriy vaziyatda O₁x₁ proyeksiyalar o‘qi tanlab olinadi, A nuqtaning yangi A″₁ proyeksiyasini yasash uchun uning A′ proyeksiyasidan O₁x₁ proyeksiyalar o‘qiga perpendikulyar o‘tkazib, uning davomiga A″A_x masofa qo‘yiladi. Natijada, A nuqtaning  tizimidagi yangi A″₁ proyeksiyasi hosil bo‘ladi. A nuqtaning A′₁ proyeksiyasini yasash uchun  tizimdan  tizimga o‘tiladi. Buning uchun ixtiyoriy vaziyatda joylashgan O₂x₂ o‘qi olinadi va nuqtaning A″₁ proyeksiyasidan O₂x₂ ga perpendikulyar o‘tkazib, uning davomiga A′A_X1 masofa qo‘yiladi. Shunday qilib O₂x₂ tizimda A nuqtaning A″₁ va A′₁ yangi proyeksiyalari hosil bo‘ladi.

167–rasmda B nuqtaning  tizimdan  va  tizimga o‘tish natijasida hosil bo‘ladigan yangi B″₁ va B′₁ proyeksiyalarini yasash ko‘rsatilgan.

Nuqtaning yangi proyeksiyalarini yasash qoidalariga asoslanib, geometrik shakllarning yangi, maqsadga muvofiq bo‘lgan proyeksiyalarini yasash mumkin.

1–masala. Umumiy vaziyatda berilgan AB(A′B′, A″B″) kesmaning haqiqiy uzunligi aniqlash talab etilsin (168-rasm).

Yechish. Buning uchun umumiy vaziyatda berilgan AB kesmaga parallel qilib gorizontal yoki frontal proyeksiyalar tekisligini yangi proyeksiyalar tekisligi bilan almashtiriladi. Chizmada masalani yechish uchun uning yangi O₁x₁ proyeksiyalar o‘qini kesmaning biror, masalan, A′B′ gorizontal proyeksiyasiga parallel qilib olinadi. Hosil bo‘lgan  proyeksiyalar tekisliklari tizimida AB kesma V₁ proyeksiyalar tekisligiga parallel bo‘ladi va bu tekislikda u haqiqiy uzunligiga teng bo‘lib proyeksiyalanadi.

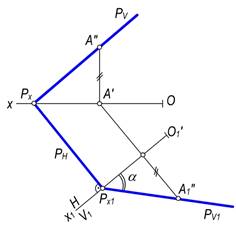
2–masala. Umumiy vaziyatdagi P(P_N, P_V) tekislikni frontal proyeksiyalovchi tekislik vaziyatiga keltirish talab etilsin (169–rasm).

Yechish. Ma’lumki, frontal proyeksiyalovchi tekislikning gorizontal izi Ox o‘qiga perpendikulyar bo‘ladi. Shuning uchun umumiy vaziyatdagi P tekislikni frontal proyeksiyalovchi vaziyatga keltirish uchun yangi O₁x₁ proyeksiyalar o‘qini tekislikning P_N gorizontal iziga ixtiyoriy joydan perpendikulyar qilib olinadi.

Tekislikning yangi P_V1 izining yo‘nalishini aniqlash uchun tekislikning P_V iziga tegishli biror, masalan, A(A′,A″) olib, uning yangi A″₁ frontal proyeksiyasi yasaladi. Tekislikning yangi P_1V izini P_x1 va A″₁ nuqtalardan o‘tkaziladi. Chizmada ko‘rsatilgan α burchak P tekislikning H tekislik bilan tashkil etgan burchagi bo‘ladi.

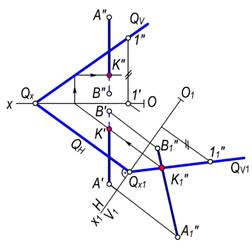
3–masala. AB(A′B′, A″B″) to‘g‘ri chiziqning umumiy vaziyatdagi Q(Q_H, Q_V) tekislik bilan kesishish nuqtasi yasalsin (170–rasm).

166-rasm.                     167-rasm.                     168-rasm.

Yechish. Masalani yechish uchun Q tekislikni gorizontal yoki frontal proyeksiyalovchi tekislik vaziyatiga keltiramiz. Buning uchun yangi O₁x₁ proyeksiyalar o‘qini tekislikning biror iziga masalan, Q_H ga perpendikulyar qilib o‘tkaziladi. Natijada, tekislikning yangi Q_V1 izini hamda to‘g‘ri chiziqning A″₁ B″₁ proyeksiyasi yasaladi. Hosil bo‘lgan kesmaning A″₁ B″₁ proyeksiyasi bilan tekislik Q_V1 izining kesishgan K″₁ nuqtasi AB kesmaning Q tekislik bilan kesishish nuqtasi bo‘ladi. Bu nuqtani teskari yo‘nalishda proyeksiyalab, berilgan to‘g‘ri chiziq kesmasi bilan tekislikning kesishish nuqtasining K′ va K″ proyeksiyalari yasaladi.

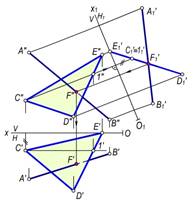
Xuddi shu usul bilan AB(A′B′, A″B″) to‘g‘ri chiziqning ∆CDE(∆C′D′E′, ∆C″D″E″), bilan kesishish nuqtasining F′ va F″ proyeksiyalarini yasaladi (171–rasm). Bunda mazkur uchburchak tekislik proyeksiyalovchi tekislik vaziyatga keltiriladi. Buning uchun chizmada ∆CDE tekislikning biror bosh chizig‘iga, masalan, C1(C′1′,C″1″) frontaliga perpendikulyar qilib yangi O₁x₁ proyeksiyalar o‘qini o‘tkaziladi. Uchburchakning C′₁D′₁E′₁ to‘g‘ri chiziq kesmasi tarzida proyeksiyalangan proyeksiyasi va kesmaning A′₁B′₁ yangi proyeksiyalari yasaladi. Ularning o‘zaro kesishgan F′₁ nuqtasi belgilanadi, so‘ngra F nuqtaning frontal F″ va gorizontal F′ proyeksiyalarini yasaladi.

169-rasm.

170-rasm.                                                           171-rasm.

4–masala. A(A′,A″) nuqtadan ∆BCD(∆B′C′D′,∆B″C″D″) tekislikkacha bo‘lgan masofani aniqlansin (172–rasm).

Echish. Bu masofa A nuqtadan ∆BCD tekislikka tushirilgan perpendikulyar bilan o‘lchanadi. Masalani yechish uchun chizmada yangi proyeksiyalar o‘qini uchburchak tekisligining asosiy chiziqlaridan biriga, masalan, gorizontaliga perpendikulyar, ya’ni O₁x₁^B′1′ qilib o‘tkaziladi. So‘ngra uchburchakning to‘g‘ri chiziq kesmasi shakldida proyeksiyalangan yangi proyeksiyalovchi D″₁B″₁C″₁ vaziyatini va nuqtaning A″₁ proyeksiyasi yasaladi. Izlangan masofaning haqiqiy uzunligi A″₁ dan D″₁B″₁C″₁ kesmaga o‘tkazilgan A″₁K″₁ perpendikulyar bo‘ladi. Bu masofaning gorizontal va frontal proyeksiyalari teskari proyeksiyalash bilan K′ va K″ proyeksiyalarni aniqlanadi. Mazkur K′ va K″ nuqtalar A nuqtaning A′ va A″ proyeksiyalaridan uchburchakning gorizontal hamda frontallariga mos ravishda tushirilgan perpendikulyarning proyeksiyalarida bo‘ladi.

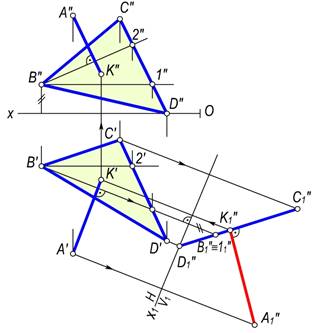
172-rasm.

5–masala. ∆ABC(∆A′B′C′, ∆A″B″C″) va ∆EFD(∆E′F′D′, ∆E″F″D″) tekisliklar kesishish chizig‘ining proyeksiyalari va uchburchaklarning ko‘rinishligi aniqlansin. (173–rasm).

Yechish. Masalani yechish uchun berilgan uchburchaklarning biri, masalan, ∆EFD ni proyeksiyalovchi vaziyatga keltiriladi. Buning uchun chizmada ∆EFD ning D′1′ va D″1″ gorizontalining proyeksiyalarini hamda unga perpendikulyar, ya’ni O₁X₁^D′1′ qilib yangi proyeksiyalar o‘qini o‘tkaziladi. So‘ngra uchburchaklarning yangi A″₁B″₁C″₁ va E″₁F″₁D″₁ proyeksiyalari yasaladi. Bunda ∆EFD ning mazkur proyeksiyasi to‘g‘ri chiziq kesmasi shaklida proyeksiyalanadi. Proyeksiyalar tekisliklarining yani tizimida ikki uchburchaklar 2″₁3″₁ to‘g‘ri chiziq bo‘yicha kesishadi. Kesishish chizig‘ining 2′3′ gorizontal va 2″3″ frontal proyeksiyalarini teskari proyeksiyalash bilan uchburchaklarning dastlabki berilgan proyeksiyalari aniqlanadi. So‘ngra chizmada topilgan 2′3′ va 2″3″ kesmalarni ∆EFD ning E′F′, E″F″ va D′F′, D″F″ tomonlari bilan kesishgan L′, L″ va T′, T″ nuqtalar aniqlanadi. Natijada, hosil bo‘lgan L′T′ va L″T″ chiziqlar ikki uchburchak kesishish chizig‘ining proyeksiyalari bo‘ladi.

Chizmada uchburchaklarning ko‘rinishligini aniqlash uchun ulardagi 4′, 4″ va 5′, 5″, shuningdek, 6′, 6″ va 7′, 7″ konkurent nuqtalardan foydalaniladi.

6–masala. ∆ABC(A′B′C′, A″B″C″) va ∆ABD(A′B′D′, A″B″D″) tekisliklari orasidagi ikki yoqli burchakning haqiqiy kattaligi aniqlansin (174–rasm).

Yechish. Bu burchak berilgan ∆ABC va ∆ABD tekisliklariga perpendikulyar bo‘lgan tekisliklar orasidagi chiziqli burchak bilan o‘lchanadi. Shuning uchun ham yangi proyeksiyalar tekisligini ikki tekislikning umumiy AB kesishish chizig‘iga perpendikulyar qilib olinadi. Lekin AB qirra umumiy vaziyayatda bo‘lgani uchun Ox,  proyeksiyalar tekisliklari tizimini avval O₁X₁, ∥AB qilib (chizmada O₁X₁∥A′B′ ), so‘ngra O₂X₂, ^AB qilib (chizmada O₂X₂^A″₁B″₁) ketma–ket almashtiriladi.

Natijada, ∆ABC va ∆ABD yangi H₁ proyeksiyalar tekisligiga perpendikulyar vaziyatda bo‘lib qoladi va o‘zaro kesishuvchi kesmalar shaklida proyeksiyalanadi. Bu kesmalar orasidagi a chiziqli o‘tkir burchak izlangan burchak bo‘ladi.

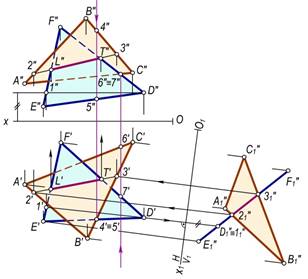
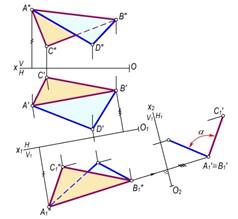
173-rasm.                                                                              174-rasm.

7–masala. AB(A′B′, A″B″) va CD(C′D′, C″D″) uchrashmas to‘g‘ri chiziq kesmalari orasidagi masofani aniqlansin (175–rasm).

Yechish. Bunda CD kesmaga parallel qilib yangi V₁ frontal proyeksiyalar tekisligi o‘tkaziladi. Bu tekislikda CD va AB kesmalarning yangi frontal proyeksiyalari C″₁D″₁va A″₁B″₁ lar yasaladi. So‘ngra C″₁D″₁ kesmaga perpendikulyar qilib N₁ tekislik o‘tkaziladi. Bu tekislikda C″₁D″₁va A″₁ B″₁ larning yangi gorizontal proyeksiyalari topiladi. Bunda CD kesma C′₁≡D′₁ nuqta ko‘rinishida proyeksiyalanadi. Bu nuqtadan A′₁ B′₁ kesmaga tushirilgan E′₁ F′₁ kesmaning uzunligi CD va AB lar orasidagi masofa bo‘ladi. Teskari proyeksiyalash bilan E va F nuqtalarning E′, E″ va F′, F″ proyeksiyalari yasalgan.

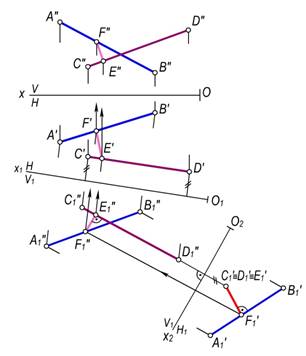
175-rasm.

Yuqoridagi masalani, birinchidan, V₁ tekislikni AB kesmaga parallel va H₁ tekislikni uning yangi proyeksiyasiga perpendikulyar qilib o‘tkazib yechsa, ikkinchidan esa  AB yoki CD kesmalardan biriga parallel qilib avval H tekislikni, so‘ngra ularning proyeksiyalaridan biriga perpendikulyar qilib V ni almashtirsa ham bo‘ladi.

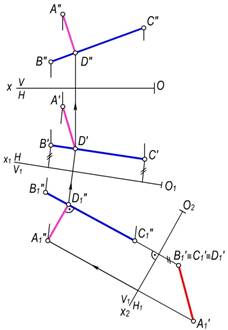
8–misol. Berilgan A(A′,A″) nuqtadan BC(B′C′, B″C″) kesmagacha bo‘lgan masofa aniqlansin (176–rasm).

Yechish. Buning uchun V tekislikni BC kesmaga parallel bo‘lgan V₁ tekislik bilan almashtiramiz, ya’ni V₁∥B′C′ sharti bajarilsin. BC kesma va A nuqtaning V₁ tekislikdagi yangi B″₁C″₁ va A″₁ frontal proyeksiyalari hosil qilinadi. So‘ngra H tekislikni H₁ tekislik bilan almashtiriladi. Bunda H₁^B″₁C″₁ bo‘lishi kerak.

H₁ tekislikda BC va A larning yangi gorizontal proyeksiyalari yasaladi. Hosil bo‘lgan A′₁ va B′₁≡C′₁ nuqtalar orasidagi masofa A nuqtadan BC kesmagacha bo‘lgan masofa bo‘ladi. Bu misolni H ni H₁∥B″C″, so‘ngra V ni V₁∥B′₁C′₁ qilib almashtirish yo‘li bilan ham yechish mumkin.

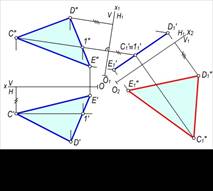
9–masala. ∆CDE(∆C′D′E′, ∆C″D″E″) uchburchakning proyeksiyalariga asosan uning haqiqiy kattaligi aniqlansin (177–rasm).

Yechish. Bunda H tekislikni H₁ tekislikka shunday almashtiramizki, H₁^∆CDE bo‘lsin. Buning uchun H₁^C″1″ (uchburchak frontalining frontal proyeksiyasi) bo‘lsa kifoya qiladi. Uchburchakning uchlarini H₁ tekislikka proyeksiyalab, yangi C′₁D′₁E′₁ gorizontal proyeksiyani to‘g‘ri chiziq ko‘rinishida hosil qilinadi. So‘ngra V tekislikni V₁ tekislik bilan shunday almashtiramizki, V₁∥C′₁D′₁E′₁ bo‘lsin. C, D, E nuqtalarning V₁ tekislikdagi yangi C″₁D″₁E″₁ frontal proyeksiyalari yasaladi. Bu nuqtalarni o‘zaro tutashtirib, ∆C″D″E″=∆CDE haqiqiy kattaligini hosil qilamiz. Bu misolni uchburchakning gorizontalini o‘tkazib va unga avval  V₁ ni perpendikulyar qilib tekislik o‘tkazish va hosil bo‘lgan kesmaga (uchburchakning proyeksiyasi) H₁ tekislikni parallel qilib o‘tkazish yo‘li bilan ham yechish mumkin.[1]

176-rasm.                                                                                        177-rasm.

Скачано с www.znanio.ru