ПЗ по теме Производная: механический и геометрический смысл производной. Уравнение касательной в общем виде.

ПЗ № 24. Производная: механический и геометрический смысл производной. Уравнение касательной в общем виде. Правила и формулы дифференцирования, таблица производных элементарных функций.

Задание:

1)Опорный конспект.

А)Механический смысл производной. Рассмотрим простейший случай: движение материальной точки вдоль координатной оси, причём закон движения задан:  координата  x  движущейся точки – известная функция  x ( t ) времени  t. В течение интервала времени от  t₀  до  t₀ +   точка перемещается на расстояние:  x ( t₀ +  ) - x ( t₀ ) = , а её средняя скорость равна:  v_a =  /  . При    0  значение средней скорости стремится к определённой величине, которая называется мгновенной скоростью  v ( t₀ )  материальной точки в момент времени  t₀ . Но по определению производной мы имеем:

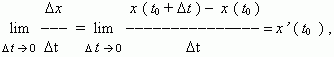
отсюда,  v ( t₀ ) = x’ ( t₀ ) , т.e. скорость – это производная координаты по времени. В этом и состоит  механический смысл производной.Аналогично, ускорение – это производная скорости по времени:  a = v’ ( t ).

Пример. Точка движется прямолинейно по закону S (t)= 2t³ – 0,5t² + 3t  (S – путь в метрах, t – время в секундах). Вычислить скорость движения точки в момент времени t=1с.

Решение: v( t ) = s ’ ( t ) = 6t² – t + 3, v(1) = 6 – 1 + 3 = 8.

Геометрический смысл производной заключается в том, что численно производная функции в данной точке равна тангенсу угла, образованного касательной, проведенной через эту точку к данной кривой, и положительным направлением оси Ох:

 Уравнение касательной. 

y =  f ( x₀ ) +  f ’( x₀ ) · ( x – x₀  ) .

Б) Пример 1. Найти производную функции   y = .

Решение: По свойству дифференцирования произведения,

.

Используя формулу для нахождения производной показательной и степенной функций, получим:  ,  

Для нахождения производной использовались правила дифференцирования и таблица производных функций.                                                                                                                                   Ответ:  .

Пример 2. Найти производную функции   y =  .

Решение: Воспользуемся правилом дифференцирования частного:

 .

Производная суммы/разности равна сумме/разности производных и константу можно выносить за знак производной, поэтому имеем:

  ,

 ,

  ,   ,    .

Ответ:     .

Пример 3. Найти производную функции     .

Решение: По свойству дифференцирования частного получаем:

 ,

 Далее пользуясь формулами для производных логарифмической и степенной функции, получим:

   ,   ,   .Ответ:   .                                                                                                           

 

Пример 4. а) Найти производную функции   .

Решение:

Примените таблицу основных производных и формулы производных линейной комбинации и отношения функций.

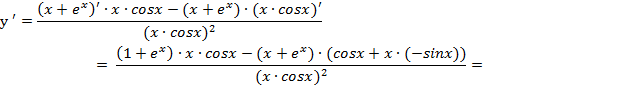
    Ответ:  .

б) Вычислить производную функции y = cos ln ().

Решение: Примените таблицу основных производных и формулу производной сложной функции.

y ^/  =   sin ln (3x² ) (ln (3x²)) ^/   =   sin ln (3x² )  ^/   =

=  sin ln (3x² )  .     

Ответ:  sin ln (3x² )  .

2)Перепишите и заполните пропуски:

А)Пример 1. Найти угловой коэффициент касательной к графику функции y = f(x) в точке с

абсциссой х₀:  а) y(x) = x³, x₀ = 1, б) y(x) = ln x, x₀ = 1, в) y(x) = 3x²  4x, x₀ = 2,

г) y(x) = х³ + 7x² 5x+3, x₀ = 3, д) y(x) = е^х, x₀ = ln 7, e) y(x) = 7sinx, x₀ = 0,ж) y(x) = е^3х, x₀ = ln 4.

Решение: угловой коэффициент k равен производной от функции в точке, т.е. k = y  ¢  (x₀) ,

найдем производные и вычислим их в точке x₀

a)    б) в)  

г)

д) е ^{ln 7}= …,е)  7cos x,  7 cos 0 = 7 1 = …, 

ж)  е^{3 ln 4}  = 34³ = 364 =  …

Ответ: a)3, б)1, в)8,г) 64,д) 7,е)7,ж) 192.

Пример 2. а) Найти угловой коэффициент k, если  α = arctg 6, α = - arctg 8.

б) Найти α,если y(x) = х³, x₀ = 2.

Решение: а) k  = tgα = tg  k  = tgα = tg  k  = tgα = tg  

k  = tgα = tg

б)

Ответ: а)1, ,6,- 8,   б) arctg 4.

Пример 3. Дана функция y = x³. Составить уравнение касательной к графику этой функции в точке x₀ = 2.
Решение: Уравнение касательной: y = f  ^¢ (x₀) · (x − x₀) + f(x₀). Точка x₀ = 2 нам дана, а вот значения f (x₀) и f  ^¢ (x₀) придется вычислять.

Для начала найдем значение функции. Тут все легко: f (x₀) = f (2) = 2³ = …;
Теперь найдем производную: f  ^¢ (x) = (x³) ^¢  = 3x²;
Подставляем в производную x₀ = 2: f  ^¢ (x₀) = f  ^¢ (2) = 3 · 2² = 34 = …;
Итого получаем: y = 12 · (x − 2) + 8 = 12x − 24 + 8 = 12x − 16. 
Это и есть уравнение касательной.

Ответ: y = 12x − 16. 
Пример 4. Составить уравнение касательной к графику функции f (x) = 2sin x + 5 в точке x₀ = π/2.

Решение:  f (x₀) = f (π/2) = 2sin (π/2) + 5 = 2 + 5 = …; f  ¢ (x) = (2sin x + 5) ¢  = 2cos x;
f ¢ (x₀) = f ¢ (π/2) = 2cos (π/2) = 0;

Уравнение касательной:   y = 0 · (x − π/2) + 7 ⇒ y = ...

Ответ: y = 7.

Пример 5. Напишите уравнения всех касательных к графику функции y = – x² – 4x + 2, проходящих через точку M(– 3; 6).

 Решение: Точка M(– 3; 6) не является точкой касания, так как f(– 3) ­ 6 (рис. ).

1. a – абсцисса точки касания.
2. f(a) = – a² – 4a + 2.
3. f '(x) = – 2x – 4, f '(a) = – 2a – 4.
4. y = – a² – 4a + 2 – 2(a + 2)(x – a) – уравнение касательной.

Касательная проходит через точку M(– 3; 6), следовательно, ее координаты удовлетворяют уравнению касательной.

6 = – a² – 4a + 2 – 2(a + 2)(– 3 – a),
a² + 6a + 8 = 0 , D = 6²  41 8 = 36  32  = …, 

а₁= (6  2) : 2 = 8 : 2  =  …,  а₂ = (6  2) : 2 = 4 : 2 = …,

Если a = – 4, то уравнение касательной имеет вид y = 4x + 18.

Если a = – 2, то уравнение касательной имеет вид y = 6.

Ответ: y = 4x + 18 или y = 6.
Пример 6. Напишите уравнения всех касательных к графику функции y = x³ – 3x² + 3, параллельных прямой y = 9x + 1.

Решение: 1. a – абсцисса точки касания. 2. f(a) = a³ – 3a² + 3.3. f '(x) = 3x² – 6x, f '(a) = 3a² – 6a.

Но, с другой стороны, f '(a) = 9 (условие параллельности). Значит, надо решить уравнение 3a² – 6a = 9. 3a² – 6a  9 = 0,

D = (6)²  43 () = 36  108  = …,  а₁= (6  12) : 6 = 18 : 6  =  …, 

а₂ = (6  12) : 6 =  6 :  6 = …,

Его корни a = – 1, a = 3 (рис. 3).

4. 1сл.) a = – 1;   f(– 1) = – 1– 3 + 3 = …;   f '(– 1) = 3 + 6 = …;

 y = – 1 + 9(x + 1);  y = 9x + 8 – уравнение касательной;

2сл.) a = 3; f(3) = 27–27 + 3 = …;  f '(3) = 27 – 18 = …;
y = 3 + 9(x – 3);  y = 9x – 24 – уравнение касательной.

Ответ: y = 9x + 8  и y = 9x – 24.

Пример 7. На параболе у = х² взяты две точки с абсциссами 1 и 3. Через эти точки проведена прямая. В какой точке параболы касательная будет параллельна проведенной прямой?

Решение: у = х² , (1;1), (3;9).  Найдем уравнение прямой .

4х – 4 = у – 1.  у = 4х – 3.

Прямые параллельны, если их угловые коэффициенты равны.

- угловой коэффициент касательной в точке с абсциссой х₀.

 2х₀ = 4.  х₀ = ...  , 

Ответ: в точке (2;4) касательная параллельна заданной прямой.

Пример 8. При каких b и c прямые y = x и y = – 2x являются касательными к графику

функции y = x² + bx + c?

Решение: Пусть t – абсцисса точки касания прямой y = x с параболой y = x² + bx + c;

p – абсцисса точки касания прямой y = – 2x с параболой y = x² + bx + c.

Тогда уравнение касательной y = x примет вид  y = (2t + b)x + c – t², а уравнение

 касательной y = – 2x примет вид y = (2p + b)x + c – p².  Составим и решим систему уравнений:

  ;

 

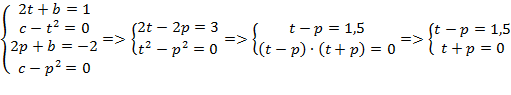2t = 1,5;  t  = 0,75;

p = – t = …,

c  =  =  = …,

b = 1 – 2t = 1 – 2  0,75 = 1– 1,5 = …

Ответ: b = – 0,5; c = 0,562 5.

Б) Пример 1. Найдите производные функций: а) y = e^x – x⁷ ,б) у=3е^х+cos2x, в) у = е^х – sinx,

г) у= – ln2x  ,д) , е) , ж) 

Решение: а)  б) в)  = е^х – cosx;  г)   ,

д)е)

ж)

Ответ: а)б) в) = е^х –cosx; г) ,

д)е)ж)

Пример 2. Вычислите значение производной функции:

а)   у=  в точке  ,  б) у=е^х sinx + x²  в точке ,

в)  у = cos2x + 4x  в точке  ,г)  в точке  .    

Решение: а)

б)          

в)   

г)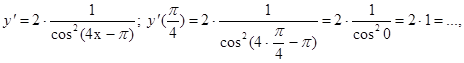 

Ответ: а)10,5; б)1;в)4; г)2.

Пример 3. Найдите производные функций: а) б)  

в)  г) д)  
Решение:  а) у ¢ (x) = (x ² + sin x) ¢ = (x ²) ¢ + (sin x) ¢ = …x + cos x;
б) у ¢ (x) = (x ³ · cos x) ¢ = (x ³) ¢ · cos x + x ³ · (cos x) ¢ = …x ² · cos x + x ³· (− sin x) =

= x ² · (3cos x − x · sin x),

в) у ¢ (x) = ((x ² + 7x − 7) · e ^x ) ¢ = (x ² + 7x − 7) ¢ · e ^x + (x ² + 7x − 7) · (e ^x ) ¢ = (2x + 7) · e ^x +

+(x ² + 7x − 7) · e ^x = e ^x · (2x + 7 + x ² + 7x−7) = (x ² + …x) · e ^x = x(x + …) · e ^x .

г)
д)

По традиции, разложим числитель на множители — это значительно упростит ответ:

Ответ: а) у ¢ (x) = 2x + cos x;  б) у ¢ (x) = x ² · (3cos x − x · sin x), в) у ¢ (x) =  x(x + 9) · e ^x ,

г) д)

Пример 4. Найти производные функций:  f(x) = e ^{2x + 3}; g(x) = sin (x ² + ln x).
Решение: Заметим, что если в функции f(x) вместо выражения 2x + 3 будет просто x, то получится элементарная функция f(x) = e ^x . Поэтому делаем замену: пусть 2x + 3 = t, f(x) = f(t) = e ^t . Ищем производную сложной функции по формуле:

f ¢ (x) = f ¢ (t) · t ¢ = (e ^t ) ¢ · t ¢ = e ^t · t ¢. Выполняем обратную замену: t = 2x + 3. Получим:

f ¢ (x) = e ^t · t ¢ = e ^{2x + 3} · (2x + 3) ¢ = e ^{2x + 3} · 2 = … · e ^{2x + 3}

Теперь разберемся с функцией g(x). Очевидно, надо заменить x ² + ln x = t. Имеем:

g ¢ (x) = g ¢ (t) · t ¢ = (sin t) ¢ · t ¢ = cos t · t ¢. Обратная замена: t = x ² + ln x. Тогда:

g ¢ (x) = cos (x ² + ln x) · (x ² + ln x) ¢ = cos (x ² + ln x) · (…x + 1/x).

Ответ:  f  ^¢ (x) = 2 · e ^{2x + 3};  g ¢ (x) = (2x + 1/x) · cos (x ² + ln x).
Пример 5. Найти производную функции :а)б)
Решение: а)

                       

б)
Ответ: а) б)

3)Решить задание  ( по примерам):А)

1.    Найти угловой коэффициент касательной к графику функции y = f(x) в точке с

абсциссой х₀:  а) y(x) = x⁴, x₀ = 1, б) y(x) = ln x, x₀ = 2, в) y(x) = 3x² - 4x, x₀ = 4,

г) y(x) = х³ + 7x² - 5x+3, x₀ =5, д) y(x) = е^х, x₀ = ln 8, e) y(x) = 9sinx, x₀ = 0,ж) y(x) = е^3х, x₀ = ln 6.

2.    а) Найти угловой коэффициент k, если  α = arctg 9, α = - arctg 11.

б) Найти α,если y(x) = х³, x₀ = 4.

3.    Дана функция y = x³. Составить уравнение касательной к графику этой функции в

точке x₀ = 1.

4.    Составить уравнение касательной к графику функции f (x) = 4sin x + 5 в точке x₀ = π/2.

5.    Напишите уравнения всех касательных к графику функции y = – x² – 4x + 2, проходящих через точку M(– 3; 9).

6.    Напишите уравнения всех касательных к графику функции y = x³ – 3x² + 3, параллельных

прямой y = 24x + 1.

7.    На параболе у=х² взяты две точки с абсциссами 1 и 2. Через эти точки проведена прямая.
В какой точке параболы касательная будет параллельна проведенной прямой?

8.         При каких b и c прямые y = x и y = – 2x являются касательными к графику
функции y = x² + 2bx + c?

Б)

1.    Найдите производные функций: а) y = 2e^x –3x⁷ ,б) у=5е^х+cos3x, в) у = е^х – cosx,

г) у= – ln4х, д) , е) , ж) 

2.    Вычислите значение производной функции:

а)   у=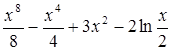  в точке  ,  б) у=2е^х sinx +3 x²  в точке ,

в)  у = cos2x + 8x  в точке  ,г)  в точке  .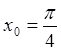    

3.    Найдите производные функций: а) б)  

в)  г) д)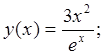  

4.    Найти производные функций:  f(x) = e ^{4x + 3}; g(x) = sin (2x ² + ln x).

5.    Найти производные функций : а)б)

4) ТЕСТ.

ЧастьА.

А₁. Найдите производную функции  y = e ^-x -2x⁷ .                                                                                               1)  y´= - e^-x -14x⁶;   2) y´= - e^-x –;  3) y´= -e^-x –2x⁶;   4) y´= e^-x -14x⁶.                                                    

А₂. Найдите производную функции   у=4х³+ е ^-х.

1) у´=12х²+е ^-х ;   2) у´=12х² – е ^-х ; 3) у´=х⁴ - е ^-х;       4) у´=12х² – хе ^-х-1.

А₃. Найдите производную функции  у = x² + sinx  в точке  х₀ =p.

     1) p² -1;     2)  2p + 1;      3) 2p -1;    4) 2p.                                                                                                   А₄. Вычислите значение производной функции   в точке х_о=2.                                    1) 10;             2) 12;             3) 8;            4) 6.

А₅. Найдите производную функции   у =  sinх e^x – 9x³ в точке x_o=0. 1) 0;   2) -1;   3) 1;   4) -9.

А₆. Найдите значение производной функции   у = 5cos x – 7x   в точке  х_о = 0 .

1) -14; 2) -7;3) -9; 4) -2.                                                                                                

А₇. Найдите производную функции  .

  1)  4х – 6+;    2) (2х - 3)²+;  3) 8х – 12 +;    4) 4х – 6 - .                                                                 А₈. Вычислите значение производной функции      в точке  х_о= 4.                          

1) 21;           2) 24;           3) 0;            4) 3,5.

А₉. Вычислите значение производной функции  y = ln(2x+11)+ 5x  в точке  х_о= -5.                                          1) 7;          2) -25;         3) 6;             4) 1.                                                                                                                                А₁₀.  Вычислите значение производной функции    в точке  х_о=  .                          

1) 1;          2) 2;            3) 0;         4) 4.

Часть В. 

В₁.Найдите производную функции:

1)  ; 2)  ;

В₂. К графику функции  проведена касательная через точку       с абсциссой . Вычислите тангенс угла наклона этой касательной к оси абсцисс.

 

Скачано с www.znanio.ru