Рабочая программа ВДУ Математическая грамотность 5 класс

 

 

 

 

 

 

Рабочая программа по внеурочной деятельности

общеинтеллектуального направления

«Основы математической грамотности»

5 класс

 

на 2020/2021 учебный год

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

СОСТАВИТЕЛЬ:

Керачинская Анна Анатольевна,

учитель математики

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

д.Старониколаево

2020 г.

 

 

Программа внеурочной деятельности для обучающихся 5 класса составлена на основе:

1. Закона «Об образовании в Российской Федерации» №273-ФЗ от 29.12.2012г    

 2. Федерального государственного образовательного стандарта основного общего образования, утв. приказом Минобрнауки России от 17.12.2010 №1897.                                                    

3. Основной образовательной программы ООО МБОУ«Кожинская СОШ»  на 2018 – 2023 гг                       

4. Программы «Развитие функциональной грамотности обучающихся основной школы: методическое пособие для педагогов». Под общей редакцией Л.Ю. Панариной, И.В. Сорокиной, О.А. Смагиной, Е.А. Зайцевой. – Самара: СИПКРО, 2019   

5. Учебного пособия для общеобразовательных организаций «Математическая грамотность. Сборник эталонных заданий» в 2-х частях. Выпуск 1. Под редакцией Г.С. Ковалевой, Л.О. Рословой, -М., СПб.: Просвещение, 2020

 

6.  PISA: математическая грамотность. – Минск: РИКЗ, 2020. – 252 с.

 

 Понятие функциональной грамотности сравнительно молодо: появилось в конце 60-х годов прошлого века в документах ЮНЕСКО и позднее вошло в обиход исследователей. Примерно до середины 70-х годов концепция и стратегия исследования связывалась с профессиональной деятельностью людей: компенсацией недостающих знаний и умений в этой сфере.

В дальнейшем этот подход был признан односторонним. Функциональная грамотность стала рассматриваться в более широком смысле: включать компьютерную грамотность, политическую, экономическую грамотность и т.д.

В таком контексте функциональная грамотность выступает как способ социальной ориентации личности, интегрирующей связь образования (в первую очередь общего) с многоплановой человеческой деятельностью.

Мониторинговым исследованием качества общего образования, призванным ответить на вопрос: «Обладают ли учащиеся 15-летнего возраста, получившие обязательное общее образование, знаниями и умениями, необходимыми им для полноценного функционирования в современном обществе, т.е. для решения широкого диапазона задач в различных сферах человеческой деятельности, общения и социальных отношений?»11, - является PISA(Programme for International Student Assessment).                     

            И функциональная грамотность понимается PISA как знания и умения, необходимые для полноценного функционирования человека в современном обществе. PISA  в своих мониторингах оценивает 4 вида грамотности: читательскую, математическую, есте-ственнонаучную и финансовую.

            Проблема развития функциональной грамотности обучающихся в России актуализировалась в 2018 году благодаря Указу Президента РФ от 7 мая 2018 г. № 204 «О национальных целях и стратегических задачах развития Российской Федерации на период до 2024 года». Согласно Указу, «в 2024 году необходимо <…> обеспечить глобальную конкурентоспособность российского образования, вхождение Российской Федерации в число 10 ведущих стран мира по качеству общего образования».

Поскольку функциональная грамотность понимается как совокупность        знаний и умений, обеспечивающих полноценное функционирование человека в современном обществе, ее развитие у школьников необходимо не только для повышения результатов мониторинга PISA, как факта доказательства выполнения Правительством РФ поставленных перед ним Президентом задач, но и для развития российского общества в целом.

Низкий уровень функциональной грамотности подрастающего поколения затрудняет их адаптацию и социализацию в социуме. Современному российскому обществу нужны эффективные граждане, способные максимально реализовать свои потенциальные возможности в трудовой и профессиональной деятельности, и тем самым принести пользу обществу, способствовать развитию страны. Этим объясняется актуальность проблемы развития функциональной грамотности у школьников на уровне общества.

Результаты лонгитюдных исследований, проведенных на выборках 2000 и 2003 гг. странами-участницами мониторингов PISA показали, что результаты оценки функциональной грамотности 15-летних учащихся являются надежным индикатором дальнейшей образовательной траектории молодых людей и их благосостояния. Любой школьник хочет быть социально успешным, его родители также надеются на высокий уровень благополучия своего ребенка во взрослой жизни. Поэтому актуальность развития функциональной грамотности обоснована еще и тем, что субъекты образовательного процесса заинтересованы в высоких академических и социальных достижениях обучающихся, чему способствует их функциональная грамотность.

 

Программа рассчитана на проведение практических занятий в объёме  35 часов в год, 1 час в неделю.

 

Результаты освоения учебного курса

Основной целью программы является развитие функциональной грамотности учащихся 8 класса как индикатора качества и эффективности образования, равенства доступа к образованию.

 

Программа нацелена на развитие:

способности человека формулировать, применять и интерпретировать математику в  разнообразных контекстах. Эта способность включает математические рассуждения, использование математических понятий, процедур, фактов и инструментов, чтобы описать, объяснить и предсказать явления. Она помогает людям понять роль математики в мире, высказывать хорошо обоснованные суждения и принимать решения, которые необходимы конструктивному, активному и размышляющему гражданину

(математическая грамотность).

 

Метапредметные и предметные

 - находить и извлекать математическую информацию в различном контексте

- применять математические знания для решения разного рода проблем

- формулировать  математическую проблему на основе анализа ситуации

- интерпретировать и оценивать математические данные в контексте лично значимой ситуации

 

Личностные результаты

- объяснять гражданскую позицию в конкретных ситуациях общественной жизни на основе математических знаний с позиции норм морали и общечеловеческих ценностей.

 

Основные виды деятельности обучающихся: самостоятельное чтение и

обсуждение  полученной информации с помощью вопросов (беседа, дискуссия, диспут); выполнение практических заданий; поиск и обсуждение материалов в сети Интернет; решение ситуационных и практико-ориентированных задач.

В целях развития познавательной активности обучающихся на занятиях   используются деловые и дидактические игры, разрабатываются и реализовываются  мини-проекты, организовываются турниры и конкурсы.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Содержание учебного курса

           

Применение чисел и действий над ними. Счет и десятичная система счисления. Сюжетные задачи, решаемые с конца. Задачи на переливание (задача Пуассона) и взвешивание. Логические задачи: задачи о «мудрецах», о лжецах и тех, кто всегда говорит правду. Первые шаги в геометрии. Простейшие геометрические фигуры. Наглядная геометрия. Задачи на разрезание и перекраивание. Разбиение объекта на части и составление модели. Размеры объектов окружающего мира (от элементарных частиц до Вселенной) длительность процессов окружающего мира. Числа и единицы измерения: время, деньги, масса, температура, расстояние. Логические задачи, решаемые с помощью таблиц. Комбинаторные задачи. Представление данных в виде таблиц, диаграмм, графиков.

 

Формы проведения занятий подбираются с учетом цели и задач, познавательных интересов, индивидуальных возможностей воспитанников:

- учебная игра;

- развивающая игра;

- тематические задания по подгруппам;

- практическое занятие;

- беседа;

- викторина;

- участие в акциях.

 

Формы контроля:

- диагностическое тестирование;

-  диагностический тренинг;

- итоговое тестирование.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Календарно-тематическое планирование

№ п\п	Дата по плану	Дата по факту	Тема урока
1			Применение чисел и действий над ними. Счет и десятичная система счисления
2			Применение чисел и действий над ними. Счет и десятичная система счисления
3			Применение чисел и действий над ними. Счет и десятичная система счисления
4			Сюжетные задачи, решаемые с конца
5			Сюжетные задачи, решаемые с конца
6			Задачи на переливание (задача Пуассона) и взвешивание
7			Задачи на переливание (задача Пуассона) и взвешивание.
8			Задачи на переливание (задача Пуассона) и взвешивание
9			Логические задачи: задачи о «мудрецах», о лжецах и тех, кто всегда говорит правду
10			Логические задачи: задачи о «мудрецах», о лжецах и тех, кто всегда говорит правду
11			Первые шаги в геометрии. Простейшие геометрические фигуры. Наглядная геометрия. Задачи на разрезание и перекраивание. Разбиение объекта на части и составление модели
12			Первые шаги в геометрии. Простейшие геометрические фигуры. Наглядная геометрия. Задачи на разрезание и перекраивание. Разбиение объекта на части и составление модели
13			Первые шаги в геометрии. Простейшие геометрические фигуры. Наглядная геометрия. Задачи на разрезание и перекраивание. Разбиение объекта на части и составление модели
14			Размеры объектов окружающего мира (от элементарных частиц до Вселенной) длительность процессов окружающего мира
15			Размеры объектов окружающего мира (от элементарных частиц до Вселенной) длительность процессов окружающего мира
16			Числа и единицы измерения: время, деньги, масса, температура, расстояние
17			Числа и единицы измерения: время, деньги, масса, температура, расстояние
18			Числа и единицы измерения: время, деньги, масса, температура, расстояние
19			Логические задачи, решаемые с помощью таблиц
20			Логические задачи, решаемые с помощью таблиц
21			Логические задачи, решаемые с помощью таблиц
22			Геометрические фигуры на клетчатой бумаге
23			Геометрические фигуры на клетчатой бумаге
24			Геометрические фигуры на клетчатой бумаге
25			Вычисление расстояний на местности в стандартных ситуациях
26			Вычисление расстояний на местности в стандартных ситуациях
27			Графы и их применение в решении задач
28			Графы и их применение в решении задач
29			Графы и их применение в решении задач
30			Комбинаторные задачи. Представление данных в виде таблиц, диаграмм, графиков
31			Комбинаторные задачи. Представление данных в виде таблиц, диаграмм, графиков
32			Комбинаторные задачи. Представление данных в виде таблиц, диаграмм, графиков
33			Проведение рубежной аттестации
34			Проведение рубежной аттестации
35			Обобщение изученного за год

 

 

Методические материалы к занятиям

5 класс

Занятие № 1-3. Применение чисел и действий над ними. Счет и десятичная система счисления

Текст для чтения:

«Различают число как результат счета элементов множества и число как результат измерения величин (длина, масса, время и т. д.)».

Но  есть много и    других источников информации, где можно познакомиться с понятием «Число».

Предлагаем познакомиться с источниками информации и прочитать определение данного понятия в предложенном тексте.

Существует большое количество определений понятию «число».

1.    В детской энциклопедии говорится, что «числа были придуманы человечеством для счета элементов реальных множеств (животных, людей, различных предметов), а также для обозначения результатов процесса измерения величин (длины, массы, емкости, времени, площади и др.)».

2. В Большой Советской Энциклопедии (выпускалась с 1926 года по 1990 год и насчитывала от 65 до 30 томов), главном справочном издании страны, в которой жили твои дедушка и бабушка – Союз Советских Социалистических республик, – про «число» говорится следующее: «…важнейшее математическое понятие. Возникну в простейшем виде ещё в первобытном обществе, понятие Число определялось потребностями счёта и измерения, возникавшими в непосредственной практической деятельности человека».

Понятие «число» используется не только в математике, но и в других областях

науки.

3.  «Число, как грамматическая категория является формой существительного,

указывающая на различное количество предметов» - говорится в словаре литературных терминов.

4. В научно–энциклопедическом словаре дается иная трактовка понятия. «ЧИСЛО

- символ, представляющий количество, используемый в расчетах и вычислениях».

5.  В  толковом  словаре    Ефремовой о числе говорится, что это «понятие, при помощи которого выражается количество и ведется счет».

6.  В Интернет издании «Википедия» «число» характеризуется как «основное понятие математики, используемое для количественной характеристики, сравнения, нумерации объектов и их частей».

Задания:

1.             Назовите основную мысль в каждом из фрагментов текста.

2.             Предложите название общего текста.

3.             Определите назначение общего текста.

4.             Укажите общую характеристику понятия «Число» в каждом фрагменте текста.

5.             Составьте вопросы к общему тексту.

6.             Продолжите фразу: «Понятие число в различных источниках объясняется по– разному. Но во всех определениях есть общий признак – это…..»

7.             Определите, к какому виду источников информации относятся книги, из которых представлен текст? Обоснуйте своё мнение.

8.             Составьте синквейн на тему « Число»

9.             Приведите примеры использования понятия «Число» в своей семье.

10.      Дайте совет своему другу, где он может воспользоваться понятием «Число».

 

 

       Занятие 4-5. Сюжетные задачи, решаемые с конца

Текст для чтения

Увлечение математикой часто начинается с размышлений над какой-то новой, интересной, нестандартной и понравившейся задачей. «Задача представляет собой требование или вопрос, на который надо найти ответ, опираясь на те условия, которые указаны в задаче, и учитывая их» (Л.М.Фридман). Задачи в которой зависимости между условием и требованием сформулированы словами называется текстовой. Сюжетная

6 (Сейчас римской нумерацией пользуются для обозначения юбилейных дат, нумерации некоторых страниц книги (например, страниц предисловия), глав в книгах, строф в стихотворениях и т.д.)

задача – текстовая задача, в которой речь идет о реальных объектах, процессах, связях и отношения. Сюжетные задачи - это наиболее древний вид школьных задач. Ещё задолго до нашей эры в Древнем Египте, Вавилоне, Китае, Индии были известны и многие методы их решения сюжетных задач существенно изменялись и видоизменяются до сих пор. Если, например, до 19-ого века цели решения этих задач были чисто практические: научить решать задачи, которые часто встречаются в жизненной практике, то затем эти цели значительно расширились и, кроме практических целей, они начинают использоваться как важное общеобразовательное и методическое средство.

Текстовая задача есть описание некоторой ситуации (ситуаций) на естественном языке с требованием дать количественную характеристику какого-либо компонента этой ситуации, установить наличие или отсутствие некоторого отношения между ее компонентами или определить вид этого отношения. (Л.П., Стойлова, А.М. Пышкало).

Под сюжетной задачей понимают задачи, в которых описан некоторый жизненный сюжет (явление, событие, процесс) с целью нахождения определенных количественных характеристик или значений (Л.П.Фридман)

Всякая задача есть требование либо на нахождение каких-либо знаний о явлениях действительности (объектах и процессах) и их характеристиках, которые они имеют в определенных заданных в задаче условиях, либо на получение какого-то искомого практического результата (построить что-то, обеспечить выполнение каких-то условий и тому подобное. ( И.И. Ильясов)

Задача представляет собой непустое множество элементов, на котором определено заранее данное отношение. (В.И. Крупич)

Вопросы для обсуждения:

-  Что нового узнали?

-       Зачем каждому из вас необходимо это знание? Где и когда вы сможете им воспользоваться?

-  Кто и зачем составляет разные задачи?

Задания:

1.             Назовите основные признаки понятий «текстовая задача», «сюжетная задача».

2.             Сформулируйте     определение     понятий:     родовой     признак     +     видовые отличительные признаки. Обоснуйте правильность вашего определения:

Текстовая задача – это … Сюжетная задача – это …

3.             Укажите компоненты ситуации как характеристики понятия «текстовая задача».

4.             Укажите    компоненты   жизненного   сюжета,    как    характеристики   понятия

«сюжетная задача».

5.             Объясните, почему понятие «задача» относится к различным областям знаниям и не только к математике.

6.             Определите, к какому типу задач («текстовая задача», «сюжетная задача») относятся представленные задачи, объясните своё мнение:

а) Космическая станция Мир оставалась на орбите в течение 15 лет и около 86 500 раз облетела вокруг Земли в течение всего срока своего полета в космосе. Самый длинный период пребывания космонавта на станции Мир длился приблизительно 680 дней. Сколько раз при этом космонавт облетел вокруг Земли?

б) Три пятых класса собрали 700кг макулатуры, 5 «А» 130 кг, 5 «Б» в 2 раза больше, сколько кг. Макулатуры собрал 5 «В»?

 

Текст для чтения:

Главным отличием задачи от примера является не только наличие текста, а наличие части условия или требования, выраженного на естественном (нематематическом) языке, которая требует в процессе решения перевода на математический язык. Например, задание «уменьшить сумму чисел 18 и 11 на 9» является текстовой задачей, а задание

«вычислить ((267-219)+33):3» является примером. Если в текстовой задаче речь идет о реальных объектах, процессах, связях и отношениях, то задача называется сюжетной. Реальные процессы – это движение, работа, покупки, смеси, сплавы и т.д.

Сюжетная задача всегда текстовая!

Сюжетные задачи различают по способам решения.

Известно несколько различных способов решения текстовых задач. Давайте назовем их:

1)  Способ рассуждений – самый примитивный способ. Этим способом решаются самые простые текстовые задачи. Его идея состоит в том, что мы проводим рассуждения, используя последовательно все условия задачи, и приходим к выводу, который и будет являться ответом задачи.

2)  Основной прием, который используется при решении текстовых задач, заключается в построении таблиц. Таблицы не только позволяют наглядно представить условие задачи или ее ответ, но в значительной степени помогают делать правильные логические выводы в ходе решения задачи.

3)            Решение задачи «с конца» – алгоритм решения задачи, когда производится обратный расчёт для вычисления каких-либо неизвестных данных на основе уже известного конечного результата.

Суть этого метода рассмотрим на следующем примере: Трое мальчиков имеют по некоторому количеству яблок. Первый мальчик даёт другим столько яблок, сколько каждый из них имеет. Затем второй мальчик даёт двум другим столько яблок, сколько каждый из них теперь имеет; в свою очередь и третий даёт каждому из двух других столько, сколько есть у каждого в тот момент. После этого у каждого из мальчиков оказывается по 8 яблок. Сколько яблок было у каждого мальчика вначале?

Рассмотрим метод решения задачи «с конца» с помощью таблицы.

 

НОМЕР МАЛЬЧИКА	1	2	3
Число яблок в конце	8	8	8
Число яблок до передачи их третьим мальчиком	8 : 2 = 4	8 : 2 = 4	8 + 4 + 4 = 16
Число яблок до передачи их вторым мальчиком	4 : 2 = 2	4 + 2 + 8 = 14	16 : 2 = 8
Число яблок первоначально	2 + 4 + 7 = 13	14 : 2 = 7	8 : 2 = 4

Таким образом, первоначально яблок у первого, второго и третьего мальчиков было соответственно 13, 7 и 4.

Таким образом,    при решении сюжетных задач, решаемых с конца, необходимо использовать следующий алгоритм:

1.       Определить конечный результат условия задачи.

2.       Определить порядок развития сюжета.

3.       Осуществить порядок действий в соответствии с развитием сюжета.

4.       Решить задачу с использованием математических операций, взаимообратных указанным в условии задачи.

Задания

1.                 Решите    задачу,    используя    предложенный    порядок    действий.    Сколько математических операций необходимо выполнить для её решения?

Магия чисел. Я задумал число, прибавил к нему 5, потом разделил сумму на 3, умножил на 4, отнял 6, разделил на 7 и получил число 2. Какое число я задумал?

2.                                      Выберите из предложенных задач сюжетные задачи, решаемые «с конца» и их решите:

а) Это старинная задача. Крестьянка пришла на базар продавать яйца. Первая покупательница купила у нее половину всех яиц и еще половину яйца. Вторая покупательница приобрела половину оставшихся яиц и еще половину яйца. Третья купила всего одно яйцо. После этого у крестьянки не осталось ничего. Сколько яиц она принесла на базар?

б) Задача из книги «Арифметика» Леонтия Магницкого. Отец решил отдать сына в учебу и спросил учителя: «Скажи, сколько учеников у тебя в классе?» Учитель ответил:

«Если придет еще учеников столько же, сколько имею, и полстолько, и четвертая часть, и твой сын, тогда будет у меня сто учеников". Сколько же учеников было в классе?»

в) Я задумал число, отнял 57, разделил на 2 и получил 27. Какое число я задумал?

3.                          Составьте синквейн на тему «Задача», «Сюжет»

4.                          Приведите примеры использования метода решения задачи «с конца» в личностном контексте.

5.                          Дай совет своему другу, где он может воспользоваться понятием

«Сюжетная задача».

Занятие 6-8.Задачи на переливание (задача Пуассона) и взвешивание

Математические задачи на переливание и взвешивания известны с древности. Сейчас их можно встретить в олимпиадных задачах или в компьютерных играх – головоломках. Классическая задача о фальшивых монетах в последнее время нашла применение в теории кодирования и информации – для обнаружения ошибки в коде.

Текст для изучения:

Задача на переливание

Эту задачу связывают с именем знаменитого французского математика, механика и физика Сименона Денни Пуассона. Когда Пуассон был еще очень молод и колебался в выборе жизненного пути, приятель показал ему тексты нескольких задач, с которыми никак не мог справиться сам. Пуассон менее чем за час решил их все до одной. Но особенно ему понравилась задача про два сосуда. «Эта задача определила мою судьбу, - говорил он впоследствии. – Я решил, что непременно буду математиком.

Рассмотрите задачу Пуассона.

Некто имеет 12 пинт вина и хочет подарить из него половину. Но у него нет сосуда в 6 пинт. У него 2 сосуда. Один в 8, другой в 5 пинт. Спрашивается, каким образом налить 6 пинт в сосуд в 8 пинт?

Заполним таблицу.

№ переливаний	0	1	2	3	4	5	6	7
12 л	12	4	4	9	9	1	1	6
5 л	0	0	5	0	3	3	5	0
8 л	0	8	3	3	0	8	6	6

 

Получаем 7 переливаний.

Задача № 1. «Бэтмен и Человек-Паук»

Бэтмен и Человек-Паук никак не могли определить, кто из них самый главный супергерой. Что только они не делали: отжимались, бегали 100-метровку, подтягивались – то один победит, то другой. Так и не разрешив свой спор, отправились они к мудрецу. Мудрец подумал и сказал: «Самый главный супергерой – это не тот, кто сильнее, а тот,кто сообразительнее! Вот, кто решит первым задачу, тот и будет самым-самым! Слушайте: имеются два сосуда вместимостью 8 л и 5 л. Как с помощью этих сосудов налить из источника 7 л живой воды?» Помогите вашему любимому герою решить эту задачу¹⁰.

Задача № 2. «Молоко из Простоквашино»

Дядя Федор собрался ехать к родителям в гости и попросил у кота Матроскина 4 л простоквашинского молока. А у Матроскина только 2 пустых бидона: трехлитровый и пятилитровый. И восьмилитровое ведро, наполненное молоком. Как Матроскину отлить 4 литра молока с помощью имеющихся сосудов? ¹¹

 Задача № 3. «Том Сойер»

Тому Сойеру нужно покрасить забор. Он имеет 12 л краски и хочет отлить из этого количества половину, но у него нет сосуда вместимостью в 6 л. У него 2 сосуда: один – вместимостью в 8 л, а другой – вместимостью в 5 л. Каким образом налить 6 л краски в сосуд на 8 л? Какое наименьшее число переливаний необходимо при этом сделать?

Задачи на взвешивание.

№5. «Буратино и Кот Базилио»

У Буратино есть 27 золотых монет. Но известно, что Кот Базилио заменил одну монету на фальшивую, а она по весу тяжелее настоящих. Как за три взвешивания на чашечных весах без гирь Буратино определить фальшивую монету?¹²

№6. «Фальшивая монета»

Среди 101 одинаковых по виду монет одна фальшивая, отличающаяся по весу. Как с помощью чашечных весов без гирь за два взвешивания определить, легче или тяжелее фальшивая монета? Hаходить фальшивую монету не требуется.¹³

№7. «Дядюшка Скрудж»

Дядюшке Скруджу принесли 8 одинаковых по виду монет, одна из которых не золотая, а фальшивая и легче других. Помогите Скруджу определить фальшивую монету. Какое минимальное число взвешиваний ему потребуется?¹⁴

 

Занятие №  9-10. Логические задачи: задачи о «мудрецах», о лжецах и тех, кто всегда говорит правду

Текст для чтения:

Среди задач на сообразительность особый интерес представляют логические задачи. Если для решения задачи требуется лишь логически мыслить и совсем не нужн

о производить арифметические выкладки, то такую задачу обычно называют логической. При решении подобных задач решающую роль играет правильное построение цепочки точных, иногда очень точных рассуждений. На первом этапе целесообразно рассмотреть три широко распространенных типа логических задач:

1.   Задачи, в которых на основании серии посылок, сообщающих те или иные сведения о действующих лицах, требуется сделать определенные выводы.

2.   Задачи о «мудрецах».

3.   Задачи о лжецах и тех, кто всегда говорит правду.

Задание: Четверо ребят – Алеша, Ваня, Боря, Гриша соревновались в беге. После соревнования каждого спросили, какое он место занял. Ребята выдали следующие ответы: Алеша: «Я не был ни первым, ни последним».

Боря: «Я не был первым». Ваня: «Я был первым».

Гриша: « Я был последним».

Три из этих ответов правильны, а один неверный. Кто сказал неправду? Кто был первым?

Вопросы для обсуждения:

-  Сколько нужно рассмотреть вариантов решения задачи?¹⁵.

-   Как легче всего оформить вариантов решения задачи? Каким средством целесообразно воспользоваться?¹⁶.

-  Как будем рассуждать?¹⁷

Задания:

1. Оформите результаты логических рассуждений в таблице¹⁸:

 

 

 

15 Четыре варианта, так как в задаче идет речь о четырех мальчиках

16 При разработке вариантов решения необходимо использовать таблицы. Пусть в каждой из таблиц один из мальчиков будет неправ, так как один из ответов данных участников неверен

17 Предположим, что, неправду сказал Алеша, а все остальные сказали правду. Тогда призовые места не

распределятся между участниками: если Алеша занимает первое место, то Ваня остается вообще без места, а если Алеша занимает четвертое место, то тогда без места остается Гриша. Следовательно, Алеша не мог соврать

18

 

1 случай	Правда	Ложь	Призовое место
Алеша	0	1	1или 4
Боря	1	0	2 или 3 или 4
Ваня	1	0	1
Гриша	1	0	4

2.    Предположите, что, неправду сказал Боря, а все остальные сказали правду. Постройте цепочку логических рассуждений. Что получится?¹⁹ Представьте данные в таблице: 3.Предположите, что, неправду сказал Ваня, а все остальные сказали правду. Постройте цепочку логических рассуждений. Что получится?²⁰. Представьте данные в таблице: 4.Предположите, что, неправду сказал Гриша, а все остальные сказали правду. Постройте цепочку логических рассуждений. Что получится?²¹. Представьте данные в таблице. 5.Сделайте вывод²².

Решение подобных логических задач.

 

Занятие 11-13. Первые шаги в геометрии. Простейшие геометрические фигуры

Текст для чтения:

За несколько столетий до нашей эры в Египте, Китае, Вавилоне, Греции уже существовали начальные геометрические знания, которые добывались в основном опытным путем и передавались от поколения к поколению в виде правил и рецептов.

Первым, кто начал получать новые геометрические факты при помощи рассуждений (доказательств), был древнегреческий математик Фалес (VIвек до нашей эры. Сочинение греческого ученого Евклида (жившего в Александрии в III веке до н.э.)

«Начало» почти 2000 лет являлось основной книгой, по которой изучали геометрию.

С геометрическими понятиями вы начинаете знакомиться с самого раннего  детства: круг, квадрат, угол, куб, измерение отрезков, площадь, объем, и т.д. При изучении фигур в геометрии не берется во внимание, из какого материала они сделаны, какого цвета, в каком состоянии находятся (твердое, жидкое, газообразное). Этим занимается физика, химия, биология. Изучая геометрию, мы будем рассматривать формы и размеры предметов.

˗                                          Шкаф, спичечный коробок, кирпич, многоэтажный дом – прямоугольный параллелепипед.

˗                                          Футбольный мяч, резиновый мяч, мыльный пузырь – шар.

˗                                          Блин, солнце, луна, озеро – круг.

˗                                          Красный кубик, синий кубик, зеленый кубик – куб.

Итак, геометрия изучает форму, размеры, взаимное расположение предметов независимо от их массы, цвета и т. д.

Вопросы для обсуждения:

¾    Как простые геометрические фигуры могут помочь современному человеку в

жизни?

¾    Как треугольник помогает при строительстве дома?

¾    Почему в окружающем мире много простых геометрических фигур?

¾    .Какие простые геометрические фигуры наиболее полезны в нашем мире?

¾    Как использовались геометрические фигуры во все времена? Использовали их до

нашего времени?

¾    Как в повседневной жизни нам помогают свойства простых геометрических фигур?

Задание:

Выполните геометрическое моделирование – воссоздание фигуры по образцу (работа в группах или парах). Для этого необходимо познакомится с танграмом:

Задания:

1. 

Сложите из двух больших треугольников квадрат, параллелограмм, большой треугольник.

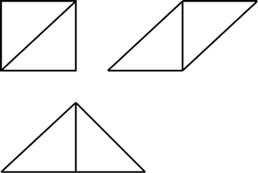Итак, складывая фигуры по-разному, мы получаем новые контуры.

2.  Сложите фигуры по заданному примеру.

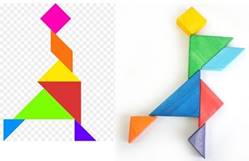3.  Воссоздайте фигуру по образцу (работа в группах): .

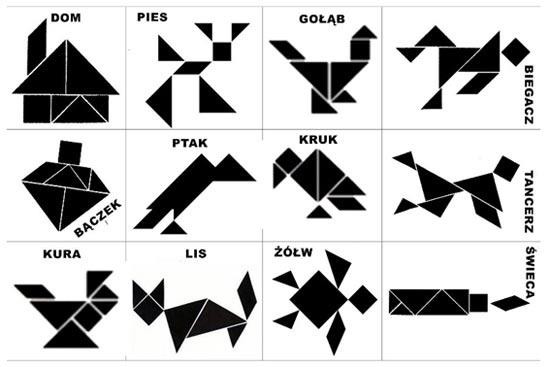
Вопросы для обсуждения:

-  Как вы думаете, какая польза может быть от этой японской игры?

-  Где и когда можно использовать это знание? Приведите примеры.

-  Какой можно сделать вывод?

Интересный факт: Особую актуальность в последнее время приобретает использование танграма дизайнерами. Самое удачное применение танграма, в качестве мебели.

 

Есть и столы-танграмы, и трансформируемая мягкая мебель, и корпусная мебель. Вся мебель, построенная по принципу танграма, довольно удобна и функциональна. Она может видоизменятся в зависимости от настроения и желания человека

Применения «танграм» в мире мы находим в современных конструкциях зданий, в которых располагаются различные жилые объекты, офисы и т. д.

 

Занятие №6. Наглядная геометрия. Задачи на разрезание и перекраивание.

Разбиение объекта на части и составление модели.

Текст для чтения

Сегодня будем решать несколько другие задачи. Известно, что с этими задачами, очевидно, столкнулся ещё первобытный человек, когда пытался раскроить шкуру убитого зверя, чтобы сшить себе одежду. Решения многих простых подобных задач были найдены ещё древними греками.

Задачами на разрезание увлекались многие ученые с древнейших времен. Решения многих задач на разрезание были найдены еще с древними греками и китайцами. Первый систематический трактат на эту тему принадлежит перу Абул-Вефа – персидского астролога X века.

Задачи на разрезание помогают как можно раньше формировать геометрические представления у школьников на разнообразном материале. При решении таких задач возникает ощущение красоты, закона и порядка в природе. На первом этапе рекомендуется рассмотреть задачи на клетчатой бумаге. Задачи, в которых разрезание фигур (в основном это квадраты и прямоугольники) идет по сторонам клеток.

Далее можно рассмотреть задачи, связанные с фигурами-пентамино. Пентамино́ изначально, (от др.-греч. πέντα пять, и домино) — пятиклеточные полимино, то есть плоские фигуры, каждая из которых состоит из пяти одинаковых квадратов, соединённых между собой сторонами («ходом ладьи»). Сегодня пентамино понимается более широко –

плоская фигура, составленная из плиток.

Задачи разбиения плоскости, в которых нужно находить сплошные разбиения прямоугольников на плитки прямоугольной формы, задачи на составление паркетов, задачи о наиболее плотной укладке фигур в прямоугольнике или квадрате, задачи, в которых одна фигура разрезается на части, из которых составляется другая фигура.

Возьмите ножницы, кроить, вырезать, соображать – вот что требуется при решении задач по геометрии ножниц.

Задачи на разрезание и перекраивание фигур.

Задания с использованием ножниц

1.                                         Перекроите фигуру, состоящую из двух квадратов, в равновеликий ей квадрат. (Для решения задачи учащимся надо найти ответ на вопрос: какие фигуры являются равновеликими? Они находят ответ либо в математическом справочнике,

либо в Интернете).

Разрезать по диагонали каждый квадрат. Диагонали будут являться сторонами получившегося квадрата.

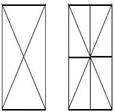2.                                        Разрежьте прямоугольник, длина которого равна 9 клеток, а ширина 4, на две равные части так, чтобы из них можно было сложить квадрат.

 

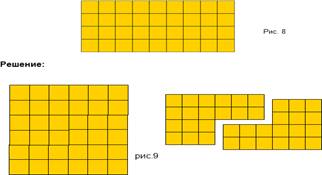
3.                                         Постройте прямоугольник со сторонами 2 см и 5 см. Разрежьте прямоугольник по диагонали. Сложите из получившихся частей треугольник.

Можно ли из этих частей сложить еще один треугольник, не равный данному? Если можно, то сложите еще один треугольник.

4.                                         Постройте прямоугольный треугольник, у которого две стороны равны. Разрежьте его на три неравные части, из которых можно было бы составить два равных квадрата.

 

Занятие № 14-15. Размеры объектов окружающего мира (от элементарных частиц до Вселенной) длительность процессов окружающего мира

Текст для чтения

Для изображения поверхности Земли на картах картографам предстояло решить математическую задачу. Нужно было уменьшить изображение и определить, какие объекты при том или ином уменьшении можно показать на географической карте.

На старинных картах и планах реальная местность показана в уменьшенном виде. Но различные участки уменьшены по-разному. Поэтому по старинным картам можно определить очертания объектов, но не их размеры. Чтобы измерить длину реки или расстояние между городами, требуется уменьшать изображение местности и всех объектов в определённое число раз. Для этого необходимо использовать масштаб.

Масштаб — это величина, которая показывает, во сколько раз расстояния на глобусе, плане или карте уменьшены по сравнению с реальными расстояниями на местности.

Масштаб — это отношение двух чисел, например \(1 : 100\) или \(1 : 1000\). Отношение показывает, во сколько раз одно число больше другого. Масштаб \(1 : 100\) означает, что изображение меньше изображаемого объекта в сто раз, а масштаб \(1 : 1000\)

—  в тысячу раз.

Чем меньше число, показывающее уменьшение, тем крупнее масштаб. Чем

больше число, показывающее уменьшение, тем мельче масштаб.

Масштаб \(1 : 100\) крупнее масштаба \(1 : 1000\) и мельче масштаба \(1 : 50\).

Масштаб на плане, карте, глобусе показывает, во сколько раз длина каждой линии уменьшена по сравнению с её действительной длиной на местности.

Так, масштаб \(1 : 100 000\) означает, что расстояние \(1\) см на плане, карте или глобусе соответствует \(100 000\) см на земной поверхности.

С помощью масштаба можно измерять расстояния между отдельными географическими объектами и определять размеры самих объектов.

Масштаб используют для создания не только планов и карт, но и копий объектов, которые выполняют с уменьшением или увеличением размеров в одном и том же соотношении.

 

Макет дома в масштабе \(1 : 500\)

Задания:

Используя данные в тексте, ответьте на вопросы.

1.   Длина отрезка на местности 4,5 км. Чему равна длина этого отрезка на карте, сделанной в масштабе 1 : 100 000?

2.   Определите расстояние по карте от устья ручья Стача до устья ручья, протекающего близ дер. Демидово. Масштаб карты 1 : 25 000.

3.    Расстояние между городами А и В на карте равно 8,5 см. Найдите расстояние между городами на местности, если масштаб карты 1 : 1 000 000.

4.   Длина железной дороги Москва – Санкт - Петербуг приближенно равна 650 км. Изобразите отрезком эту дорогу, применив масштаб 1 : 10 000 000.

4) Расстояние от Бреста до Владивостока более 10 000 км. Уместится ли на одной страницы тетради это расстояние при масштабе одна десятимиллионная?

5) На рисунке дан план квартиры в масштабе 1 : 100. Определите по плану, какие размеры имеют кухня, ванная и комнаты и какова их площадь в действительности.

6) Отрезку на карте длиной 3,6 см соответствует расстояние на местности в 72 км. Каково расстояние между городами, если на это карте расстояние между ними 12,6 см?

7) Длина железнодорожной магистрали 6140 км. Какой длины получится линия, изображающая магистраль на карте, сделанной в масштабе: а) 1 : 10 000 000; б) 1 : 2

000 000.

8) Отрезок на местности длиной 3 км изображен на карте отрезком 6 см. Какова на карте длина отрезка, изображающего отрезок 10 км? Какой отрезок на местности изображает отрезок на карте длиной 1,8 см?

9) Длина детали на чертеже, сделанном в масштабе 1 : 5, равна 7,2 см. Чему будет равна длина этой детали на другом чертеже, сделанном в масштабе 1 : 3? В масштабе 2 : 1?

Занятие 16-18. Числа и единицы измерения. Время, деньги, масса, температура, расстояние

Рассмотрите задания и ответьте на вопросы:

Задание 1. В 6 часов утра в воскресенье гусеница начала вползать на дерево. В течение всего дня, т. е. до 18 часов, она вползла на высоту 5 метров, а в течение ночи спустилась на 2 метра. В какой день и час она вползет на высоту 9 метров?

A)  в понедельник в 18 часов

B)  во вторник в 7 часов

C)  во вторник в 13 часов 12 минут

D)  в среду в 16 часов 25 минут

E)  в среду в 21 час

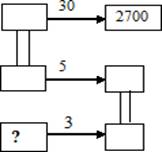
Задание 2. На 30 самолетах Ту-134 можно перевести 2700 пассажиров. В пяти самолётах Ту-134 помещается столько пассажиров, сколько в трёх самолётах Ту- 154. Сколько пассажиров можно перевести на самолёте Ту – 154?

 

Задание 3. Автобус из с. Камышла до г. Самара едет 3 часа 10 минут, а обратно – … минут. Объясни, почему?

A)  2 ч 10 мин  B) 250 минут   C) 1 час 20 мин  D) 2 часа 5 мин    E) 190 мин

Задания:

1.       Найдите в представленных задачах математическую информацию.

2.       Запишите из условия задачи: число и величину.

3.       Назовите признаки отличия: числа и величины.

4.       Нарисуйте в виде множества, какое понятие входит в область другого понятия

(множественное отношение).

5.       Дополнить схему на темы: «Число» и «Величина».

 

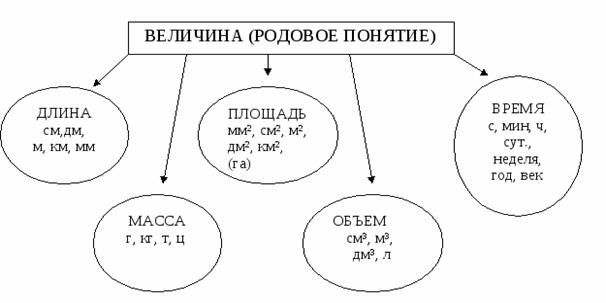
6.                                                                                                Прочитайте текст, исправьте ошибки.

Занимательные задачи

 

1)На скамейке сидел дед И было деду 20 лет	2) Я дверь закрыла на засов. На улице ночь, время 16 часов.
3) Коля в 1 класс пошёл. Он считает хорошо. Он сказал ребятам весело: «Мне сейчас 48 месяцев».	4) Таня спать ложиться в 8. Тане в 9 надо встать. Завела будильник в 9. И спокойно будет спать.

 

 

7.  Составьте задания: с понятием числа; с понятием величины; с понятиями числа и величины.

Занятие № 19-21 «Логические задачи, решаемые с помощью таблиц»

1. В кафе встретились три друга: скульптор Белов, скрипач Чернов и художник Рыжов. “Замечательно, что один из нас имеет белые, один черные и один рыжие волосы, но ни у одного из нас нет волос того цвета, на который указывает его фамилия”, - заметил черноволосый. “Ты прав”, - сказал Белов. Какой цвет волос у художника?

Решение. Для решения подобных логических задач полезно составить таблицу.

 

 

Ответ.

 

 

В бутылке, стакане, кувшине и банке находятся молоко, лимонад, квас и вода. Известно, что вода и молоко не в бутылке, сосуд с лимонадом стоит между кувшином и сосудом с квасом, в банке – не лимонад и не вода. Стакан стоит около банки и сосуда с молоком.

Куда налита каждая жидкость?

Ответ.

 

 

Занятие № 22-24 «Геометрические задачи на построение и на изучение свойств фигур: геометрические фигуры на клетчатой бумаге, конструирование» - Методические разработки Козлова С.А., Рубин А.Г. Математика. Учебник для 6 класса. В 2-х частях. Часть 2. – М.: Баласс, 2011. (Образовательная система «Школа 2100»)

 

Занятие № 25-26 «Вычисление расстояний на местности в стандартных ситуациях»

 

Текст для чтения:

Иван приобрел автомобиль и решил покататься. Он ехал 12 минут со скоростью

60км/ч, затем Иван выехал за город и проехал 20 минут со скоростью 90 км/ч.

Вопросы для обсуждения

- Какие вопросы можно задать к этому тексту, чтобы он получился задачей?

- К какому типу относится эта задача?

- Какие математические знания и практические умения помогут нам решить эту задачу?

- С помощью каких формул можно найти ответы на вопросы задачи?

Задание: Решите задачу, ответив на вопрос «С какой средней скоростью проехал Иван весь путь?» (Округлите полученный ответ до целого числа). Можно ли с такой скоростью двигаться в черте

 

Занятие № 27-29 «Графы и их применение в решении задач»

Задача 1 «Муха в банке»:

Муха забралась в банку из-под сахара. Банка имеет форму куба. Сможет ли муха последовательно обойти все 12 ребер куба, не проходя дважды по одному ребру? Подпрыгивать и перелетать с места на место не разрешается.

Решение: Ребра и вершины куба образуют граф, все 8 вершин которого имеют кратность 3, и, следовательно, требуемый обход невозможен.

Задача 2:

Какие буквы русского алфавита можно нарисовать одним рос­черком?

Ответ: Б, В, Г, 3, И, Л, М, О, П, Р, С, Ф, Ъ, Ь, Я – 15 букв.

Задача 3 «Головоломка Сема Лойда»:

Во дворе, который окружен высоким забором, находятся три домика: красный, желтый и синий. В заборе есть три калитки: красная, желтая и синяя. От красного домика проведите дорожку к красной калитке, от желтого домика – к желтой калитке, от синего – к синей так, чтобы эти дорожки не пересекались.

Решение:

 

 

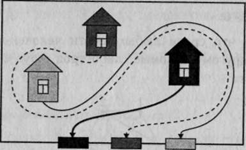
Задача 4 «Головоломка Генри Дыодени»:

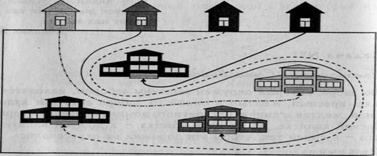
Четыре школьника, которые живут в желтом, зеленом, синем и красном домах, ходят в разные школы. Однажды, на свежем снегу особенно хорошо было видно, что следы четырех мальчиков нигде не пересекают друг друга и не выходят за пределы границ. Возьмите карандаши и продолжите их пути так, чтобы каждый мальчик из своего дома попал в школу такого же цвета, что и его дом.

 

Решение:

 

 

Занятие № 30-32 «Комбинаторные задачи представление данных в виде таблиц диаграмм графиков»

 

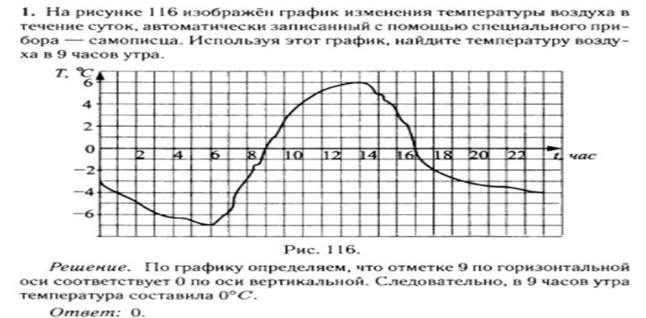
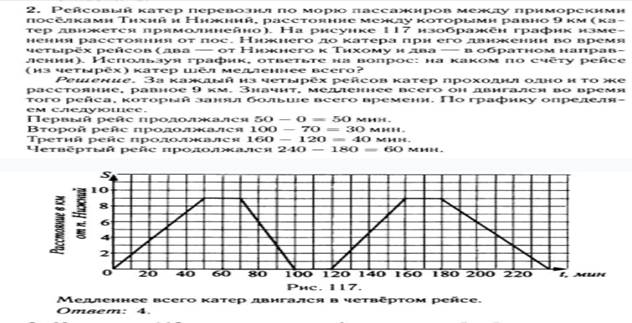
4.  Шестиклассник Миша и его семья - мама, папа и сестренка Алёнка 6 лет от роду запланировали во время школьных каникул отдохнуть за границей. Бюджет семьи позволяет потратить на поездку не более 60 000 рублей. Цены на горящие туры, предложенные семье одним из турагенств, приведены в таблице:

Страна	Стоимость тура на 6 дней за 1 чел. (руб.)	Коли-чество чело-век	Общая стоимость тура (руб.)	Общая стоимость тура с учетом 50% скидки на детей
Турция	13 403	4		-
Венгрия	10 625	4		-
Абхазия	16 485	4		-
Чехия	20 221	4		-
Испания	24 804	4

Заполните выделенные цветом ячейки таблицы и ответьте на вопросы:

1.Какие страны сможет себе позволить в этом году посетить семья Миши. Ответ:___________________________________

2. Сможет ли данная семья приобрести путевку в Испанию, чтобы попасть на карнавал на Тенерифе, если турагенство представляет детям до 16 лет скидку 50% на путевку в данную страну? В ответ запишите стоимость этой путевки в рублях Ответ:___________________________

Занятие № 30-32. Комбинаторные задачи. Представление данных в виде таблиц, диаграмм, графиков.

Текст для чтения:

Люди изучают окружающий их мир. Проводят научные исследования. Производят много полезных вещей. Выращивают сельскохозяйственную продукцию. Выполняя все это, они собирают данные. Эти данные нужно грамотно записать и представить так, чтобы с ними можно было удобно работать: выбрать нужные данные, сравнивать их, анализировать

Математические средства представления информации: таблицы, диаграммы, графики, формулы. Представление информации (особенно статистической) в виде диаграмм и графиков позволяет удобно и быстро считывать эту информацию с целью её анализа или прогноза на будущее. Поэтому умение читать графики  и  диаграммы является одним из базовых для адаптации человека в социуме.

Наиболее удобно представлять данные с помощью таблиц.

Ты уже знаком с некоторыми таблицами и активно ими пользуешься. Вспомните и приведите примеры использования таблиц для представления данных в личностном контексте.

                              

 

Таблица умножения

Дневник

Расписание

С таблицами работать не всегда удобно. Сегодня ты познакомишься с более простым способом представления данных. Это диаграммы.

Диаграмма – это один из способов наглядного представления различных числовых данных. На диаграммах числа или значения величин могут изображаться отрезками, столбиками, частями круга или другими фигурами.

Диаграмма (греч. Διάγραμμα (diagramma) — изображение, рисунок, чертеж) — графическое представление данных, позволяющее быстро оценить соотношение нескольких величин. Представляет собой геометрическое символьное изображение информации с применением различных приёмов техники визуализации. Виды диаграмм: круговые или секторные; столбчатые и линейные диаграммы (гистограммы); точечные; кольцевые; лепестковые и другие.

Исследовательская работа: научиться строить диаграммы.

Пятиклассники провели исследование «Мой любимый цветок». Девочкам задали вопрос: «Какой у тебя любимый цветок?». Результаты опроса представлены в таблицу.

Цветок	Количество девочек
Ромашка	5
Роза	8
Лилия	4
Тюльпан	3

По этой таблице можно построить диаграмму. Она будет выглядеть так.

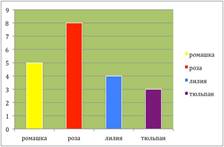
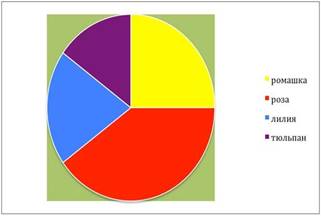
Диаграммы используют в том случае, когда данные нужно представить наглядно. Диаграммы часто используются для иллюстрации различных данных в учебниках, научных книгах, журналах.

.

Рассмотрите задание.

В мире много красивых городов. Среди них Санкт-Петербург, Москва, Париж, Венеция, Прага, Лондон. В них много замечательных зданий, памятников, мостов. Провели исследование «Сколько мостов?» и данные записали в таблицу.

Город	Количество мостов
Санкт-Петербург	342
Москва	76
Париж	37
Прага	18
Венеция	400
Лондон	32

По данным таблицы построили диаграмму.

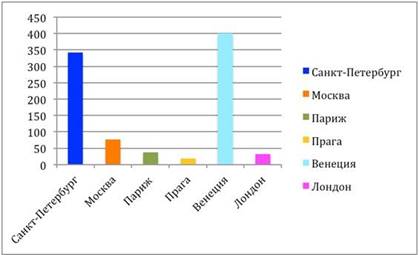
Задания:

1.         Назовите средства представления информации в повседневной жизни человека.

2.         Укажите, какие виды диаграмм можно использовать для представления информации.

3.         Приведите    примеры    представления    информации    в    виде    таблицы,    диаграммы (столбчатой или круговой), в вашей семье, в школьной жизни.

4.         Составьте кластер на тему «Диаграмма».

5.         Дай совет своему другу, где он может воспользоваться понятием «Диаграмма».

6.         Используя игровую ситуацию, помогите героям сказки Вини-Пуху, Ослику, Пятачку, Сове и Кролику научиться экономить электроэнергию.

7.             Предыдущее показание счетчика в домике Вини-Пуха составило 350 кВт×ч, а последнее показание – 500 кВт×ч. Сколько кВт×ч электроэнергии израсходовал медвежонок? Сколько денег должен заплатить Вини за электроэнергию, если 1 кВт×ч стоит 100 лесных рублей?

·                     Предыдущее показание счетчика в домике Пятачка составило 270 кВт×ч, а последнее показание — 370 кВт×ч. Сколько кВт×ч электроэнергии израсходовал поросенок? Сколько денег должен заплатить Пятачок за электроэнергию, если 1 кВт×ч стоит 100

·                     Предыдущее показание счетчика в домике Совы составило 380 кВт×ч, а последнее показание — 450 кВт×ч. Сколько кВт×ч электроэнергии израсходовала Сова? Сколько денег должна заплатить она за электроэнергию, если 1 кВт×ч стоит 100 лесных рублей?

·         Предыдущее показание счетчика в домике Ослика Иа составило 350 кВт×ч, а последнее показание – 440 кВт×ч. Сколько кВт×ч электроэнергии израсходовал Иа? Сколько денег должен заплатить Ослик за электроэнергию, если 1 кВт×ч стоит 100 лесных рублей?

·         Предыдущее показание счетчика в домике Кролика составило 360 кВт×ч, а последнее показание — 420 кВт×ч. Сколько кВт×ч электроэнергии израсходовал он? Сколько денег должен заплатить Кролик за электроэнергию, если 1 кВт×ч стоит 100 лесных рублей?

8.         Составьте таблицу, используя информацию из текста

 

Герой сказки	Кол-во потребленной электоэнергии (кВт×ч)	Тариф (лесные рубли)	Сумма оплаты (лесные рубли)
Вини-Пух
Пятачок
Сова
Ослик Иа
Кролик

9.  Постройте диаграмму по сумме оплаты за электроэнергию. 10.Ответьте, используя диаграмму на вопросы:

 –     Кто из героев сказки является самым экономным?

–    Самым расточительным?

 

 

Рассмотрено на заседании ШМО

Руководитель ШМО

_________________ /_________________/

Протокол №_________

От   «_____»  ______________20_____

 

 

 

 

 

 

Согласовано

Заместитель директора по УВР

_____________________ /А.А. Керачинская/

«_____»  ____________________20___

Скачано с www.znanio.ru