Рабочая тетрадь и рекомендации по учебной дисциплине "Математика"

МИНИСТЕРСТВО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ И ЗАНЯТОСТИ НАСЕЛЕНИЯ ПРИМОРСКОГО КРАЯ

ФИЛИАЛ КРАЕВОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО

ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ

«УССУРИЙСКИЙ АГРОПРОМЫШЛЕННЫЙ КОЛЛЕДЖ»

В ХАНКАЙСКОМ РАЙОНЕ

 

 

 

 

 

 

 

 

Рабочая   тетрадь И РЕКОМЕНДАЦИИ

по учебной дисциплинЕ «Математика»

для студентов I,2 курса по профессии:

 43.01.09 «Повар, кондитер»,

35.01.27 «Мастер сельскохозяйственного производства»

по самостоятельному изучению тем по математике

 

 

 

 

 

                          

 

 

 

 

 

 

 

 

 

 

Разработал:	Рассмотрено:	Утверждаю:
Гуржий В. И.   Подпись: _______________	На заседании ЦК общеобразовательных дисциплин Председатель: Рыжих Т. М. Протокол № от «__» ___ 2022г. Подпись: _____________	Заведующий учебно- производственной частью Милякова Д.В. «__» ______2022г. Подпись: _______________

 

 

 

 

 

 

 

Аннотация

 Данная рабочая тетрадь предусматривает оказание помощи обучающимся 1,2 курса в самостоятельном изучении разделов математики. Рассматриваются вопросы по разделу: «Математика».

  В начале изучения темы даются рекомендации по её изучению, указывается   параграф в учебной литературе, предлагаются упражнения для проверки знаний по изученному материалу, а затем дается задание или тест контроля знаний.

 Для изучения материала делаются ссылки на учебник для 10-11 классов «Алгебра и начала анализа» /Ш.А.Алимов, Ю.М.Колягин, Ю.В.Сидоров –М. Просвещение, 2012.  А.Н.Колмогоров «Алгебра и начала анализа. Просвещение, 2010г.

Математика: учебник для учреждений нач. и сред. проф. образования.  Башмаков М.И.   М: Издательский дом «Академия», 2020г.

Математика. Задачник: учеб. Пособие для учреждений нач. и сред. проф. образования. Башмаков М.И.   М: Издательский дом «Академия», 2020г.

 Студент может пользоваться и другой учебной литературой.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 Тема №1 «Степень с рациональным показателем».

 

Для усвоения данной темы следует изучить материал § 5, усвоить свойства степени с рациональным показателем, рассмотреть решение задач 1-10, выполнить задания: №№ 56, 58, 60,69,76, 77.

 

                                       С в о й с т в а   с т е п е н и:

 

1.Для n-натурального, m-целого (а> 0) справедливо равенство

                                    

 

2.          

 

3.        

 

4.        

 

5.        

 

6.          

 

7.          .   Рассматриваемые p, q –рациональные

                                                        числа.

 

                                        Контроль знаний №1.

 

1.Представить в виде степени с рациональным показателем:

      a).    

      b).    

      c).     

      d).     

 

2.Упростить:

 

      a).      

 

      b).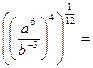       

      c).      

 

 

 

3.Вычислить:

 

      a).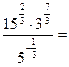      

 

      b).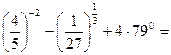      

 

      c).        

 

      d).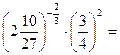       

4.Решить    уравнения:    a).        .___________________________

 

                                              b).        .___________________________

 

                                              c).        .__________________________

 

                                              d).        . __________________________

    

 

Тема № 2. «Показательная функция»

 

Следует изучить материал §§11, 12, 13.  Рассмотреть решения задач 1-8

из § 12 и выполнить задания №№ 208, 210, 211, 213, 215,217, 218.

Рассмотреть решения задач 1-6 из § 13 и выполнить задания №№ 228, 231, 232, 233, 239.

 

 

                                     Контроль знаний №2.

 

1.Решить уравнения:

а).   __________________________________________________

б).      __________________________________________________

в).      __________________________________________________

 

г).  ;    __________________________________________________

 

д).  __________________________________________________

 

е).  _________________________________________________

 

ж).     __________________________________________________

 

з).  ______________________________________________

 

и).  ________________________________________________

 

к).  _____________________________________________

 

2.Решить неравенства:

 

а). ______________________________________________________

 

б). ____________________________________________________

в).  ____________________________________________________

г). ____________________________________________________

 

д). ; _________________________________________________

         Тема № 3.  «Логарифмическая функция».

 

Следует хорошо усвоить понятие логарифма  и основные логарифмические тождества (§ 15), решить задания №№ 267-277,  №№ 279-281.

Свойства логарифмов даны в §§ 16, 17, закрепить данный материал можно, решив №№ 290 -294, 297, 298,307.

Чтобы иметь представление о решении логарифмических уравнений и неравенств, следует знать и  уметь строить графики  логарифмической функции (§ 18).

С примерами решения логарифмических уравнений и неравенств следует ознакомиться в задачах  1- 7( § 19),  1-3 (§ 20).

Для закрепления материала решить №№ 337-340, 343, 344, 348, 349, 355-357, 359-364.

 

     Понятие логарифма:

«Логарифмом положительного числа  b  по основанию  а,   где  а0,  а≠ 1, называется показатель степени, в которую надо возвести число а, чтобы получить b.»                     

 

     Два основных тождества:         1).   

                                                          2).    

 

     Свойства логарифмов:      1.   

                                                 2.   

                                                 3.    

                                              4.   

                                              5.   

                                              6.   

                                              7.   

                                              8.   

 

 

     Десятичным логарифмом числа  называют логарифм этого числа по основанию 10 и пишут  lg b  вместо        

 

     Натуральным логарифмом числа  называют логарифм этого числа по основанию   е,  где   е   - иррациональное число, приближенно равное  2,7. При этом пишут  ln b,  вместо   

 

                                Контроль знаний № 3.

1.Вычислить:

 1).   

 

 

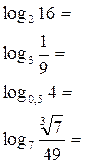
 2).  

 

 

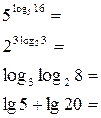
3).   

 

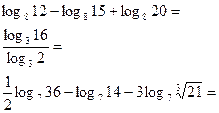
2. Решить уравнение:

    1).  _______________________________________________

    2).  ___________________________________________

    3).  ______________________________________

    4).  ________________________________________

 

3.Решить неравенство:

     1).  ___________________________________________

 

     2).      ___________________________________________

     3).          ___________________________________________

 

     4).  _____________________________________

 

     5).   _____________________________________

 

Тема № 4 «Тригонометрия».

 

Для изучения этой большой, сложной темы необходимо:

повторить:

- понятия тригонометрических функций для острого угла прямоугольного треугольника;

-значения тригонометрических функций для углов 30, 45  и  60;

-основные тригонометрические тождества;

изучить §§ 21-29, 31,32;

  уметь использовать понятия, определения и формулы тригонометрии при упрощении и вычислении выражений с тригонометрическими функциями;

  изучить  §§  33-43;

  знать и уметь определять обратные тригонометрические функции;

  уметь решать тригонометрические уравнения и неравенства;

 

 

                            Контроль знаний № 4.

 

1. Синусом острого угла прямоугольного треугольника называется………...

     ______________________________________________________________

2. Косинусом острого угла прямоугольного треугольника называется ……..

     ______________________________________________________________

3.  Тангенсом острого угла прямоугольного треугольника называется ……..

     ______________________________________________________________

4.  Котангенсом острого угла прямоугольного треугольника называется ….

     ______________________________________________________________

 

5.Заполнить недостающие данные таблицы на основании градусной и

    радианной меры углов.

Градусы	30		60			120	210			270		360
Радианы

 

6.  Синусом любого угла        называется …………………………………….

     ______________________________________________________________

 

7.  Косинусом любого угла        называется ………………………………….

     ______________________________________________________________

 

 

 

8.  Определить знак выражения:

 

А).       _________________

Б).           _________________

 

9. Вычислить    если         и    

    ______________________________________________________________

    ______________________________________________________________

    ______________________________________________________________

 

10. Упростить выражение:

 

А).     ____________________________________________

 

Б).   ____________________________________________

 

В).  ________________________________________

 

Г).  __________________________________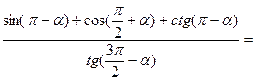

       _____________________________________________________________

 

11. Вычислить:

 

А). __________________________________________

Б).  _______________________________

        ____________________________________________________________

 

В).   _________________________________

        ________________________________________________________________

 

Г).  ______________________________________

 

Д).    _____________________________________________

 

Е).  ___________________________________________

 

                              Контроль знаний №5

 

1.Вычислить:

 

А).  _________________________________

 

Б).    ____________________________________________

 

В).    ______________________________________________

 

Г).     ______________________________________________

 

2.Решить уравнения:

 

А).    ___________________________________________________

Б).    _________________________________________________

В).      _________________________________________________

 

Г).      _________________________________________________

 

Д).   ___________________________________________

 

Е).     ______________________________________________

 

Ж).  _________________________________________

         ____________________________________________________________

 

З).    ____________________________________________

         ____________________________________________________________

 

И).      ____________________________________________

         ____________________________________________________________

 

К).     _____________________________________________

 

Л).    ___________________________________________

        ____________________________________________________________

 

М).  ____________________________________

        ___________________________________________________________

              Тема №5 «Производная и ее геометрический смысл».

 

     По учебнику изучить материал §§ 44-52. В результате студент должен: знать:

-определение производной;

-правила дифференцирования;

-производные некоторых элементарных функций;

-геометрический смысл производной;

-признаки возрастания и убывания функции;

уметь:

-находить производную функций с использованием правил и формул;

- находить производную сложной функции;

-применять производную к исследованию функций и построению

 графиков.

 

                                     Контроль знаний  №6.

 

1.Производной функции  f(x) в точке  х  называется…………………………..

   _______________________________________________________________

 

2.Найти производную функции

  

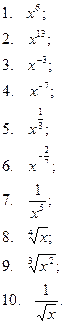
3.Найти , если

  1).    ______________________________________________

  2). ,  ______________________________________________

  3). ,  ______________________________________________

  4). ,  ___________________________________________

       _____________________________________________________________

 

                              Контроль знаний № 7.

 

1.Найти производную функции:

   1). ________________________________

 

   2). _______________________________

 

   3). _______________________________

   4). _____________________________

 

   5). ___________________________________________

 

   6). _______________________________________________

 

   7). _________________________________________________

 

   8). __________________________________________

 

   9).  _______________________________________________

 

  10). ____________________________________________

 

  11).  ________________________________________

 

  12).  ___________________________________________________

 

2.Найти угол между касательной к графику функции  f(x)=sin x   в точке c

   абсциссой  _______________________________________________

    ______________________________________________________________

 

3.Написать уравнение касательной к графику функции  f(x)=  в точке

   абсциссой    _______________________________________________

    ______________________________________________________________

 

4.Найти точки экстремума функции       __________________

 

 

 

                                   Тема № 6.  «Интеграл».

 

        Изучить материал    §§ 54-58 рекомендуемого учебного пособия. В результате студент должен:

Знать:

-понятие первообразной;

-правила нахождения первообразных;

-формулу Ньютона-Лейбница;

Уметь:

-находить первообразные для заданных функций;

-находить площади криволинейной трапеции;

-вычислять определенные интегралы;

-применять интеграл к решению практических задач.

 

                         Контроль знаний №8.

 

1.Функция  F(x)  называется первообразной для функции  f(x) на некотором

   промежутке, если………………………………………………………………

 

2.Заполните таблицу первообразных

                               

Функция	Первообразная

 

3.Криволинейной трапецией называется……………………………………….

 

                                   Контроль знаний  № 9.

 

1.Доказать, что функция   F(х)=     есть  первообразная  для  функции      f =     на  промежутке  .

 

 

2.Найти первообразную для функции  f(x)=3sin x-2cos x.

 

 

 

3.Для функции     f(x)=  найти первообразную, график которой проходит

    через точку  М(1; -1).

________________________________________________________________

 

 

4.Вычислить:

  1)._______________________________________________________

 

  2). _____________________________________________________

 

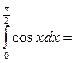  3). ___________________________________________________

 

  4).   ___________________________________________________

 

5.Найти площадь фигуры, ограниченной линиями

          

 

 

 

 

6.Найти объем тела, полученного при вращении вокруг оси абсцисс

   криволинейной трапеции, ограниченной линиями

                 у=2х+1,  х=0, х=2, у=0.