Утверждаю

_____________      

Директор                                                                                                 

Н.Ю.Прокофьева                                                                                     

Рабочая программа по алгебре в 7 классе

(базовый уровень) на  2017-2018 учебный год

муниципального бюджетного общеобразовательного учреждения Гимназия №3

городского округа город Шарья Костромской области

Пояснительная записка

Рабочая программа основного общего образования по алгебре составлена на основе Фундаментального ядра содержания общего образования и Требований к результатам освоения основной общеобразовательной программы основного общего образования, представленных в Федеральном государственном образовательном стандарте общего образования. В ней также учитываются основные идеи и положения Программы развития и формирования универсальных учебных действий для основного общего образования.

Сознательное овладение учащимися системой алгебраических знаний и умений необходимо в повседневной жизни, для изучения смежных дисциплин и продолжения образования.

Практическая значимость школьного курса алгебры обусловлена тем, что ее объектом являются количественные отношения действительного мира. Математическая подготовка необходима для понимания принципов устройства и использования современной техники, восприятия научных и технических понятий и идей. Математика является языком науки и техники. С ее помощью моделируются и изучаются явления и процессы, происходящие в природе.

Алгебра является одним из опорных предметов основной школы: она обеспечивает изучение других дисциплин. В первую очередь это относиться к предметам естественно-научного цикла, в частности к физике. Развитие логического мышления обучающихся при обучении алгебры способствует усвоению предметов гуманитарного цикла. Практические умения и навыки арифметического характера необходимы для трудовой и профессиональной подготовки школьников.

Развитие у обучающихся правильных представлений о сущности и происхождении арифметических абстракций, о соотношении реального и идеального, характере отражения математической наукой явлений и процессов реального мира, месте алгебры в системе наук и роли математического моделирования в научном познании и в практике способствует формированию научного мировоззрения обучающихся и качеств мышления, необходимых для адаптации в современном информационном обществе.

Требуя от обучающихся умственных и волевых усилий, концентрация внимания, активности развитого воображения, алгебра развивает нравственные черты личности и умение аргументировано отстаивать свои взгляды и убеждения, а также способность принимать самостоятельные решения. 

Изучение алгебры, функций, вероятности и статистики существенно расширяет кругозор обучающихся, знакомя их с индукцией, обобщением и конкретизацией, анализом и синтезом, классификацией и систематизацией, абстрагированием, аналогией. Активное использование задач на всех этапах учебного процесса развивает творческие способности школьников.

Изучение алгебры позволяет формировать умения и навыки умственного труда - планирование своей работы, поиск рациональных путей ее выполнения, критическую оценку результатов. В процессе изучения алгебры школьники должны научиться излагать свои мысли ясно и исчерпывающе, лаконично и емко, приобретают навыки четкого, аккуратного и грамотного выполнения математических записей.

Важнейшей задачей школьного курса алгебры является развитие логического мышления обучающихся. Сами объекты математических умозаключений и принятые в алгебре правила их конструирования способствуют формированию умений обосновывать и доказывать суждения, приводить четкие определения, развивают логическую интуицию, кратко и наглядно раскрывают механизм логических построений и учат их применению. Тем самым алгебра занимает одно из ведущих мест в формировании научно-теоретического мышления школьников. Раскрывая внутреннюю гармонию математики, формируя понимание красоты и изящества математических рассуждений, алгебра вносит значительный вклад в эстетическое воспитание обучающихся.

Общая характеристика учебного предмета

 Тематическое планирование по алгебре 7 класса составлено по примерной программе общеобразовательных учреждений. Алгебра. 7 – 9 классы. Составитель: Т.А. Бурмистрова. М.: «Просвещение», 2014 г.

Данное планирование направлено на достижение требований ФГОС и ориентирована на использование учебника «Алгебра» 7 класса Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова. М.:«Просвещение», 2017 г.

В курсе алгебры7 класса можно выделить следующие основные содержательные линии: арифметика; алгебра; функции; вероятность и статистика. Наряду с этим в содержание включены две дополнительные методологические темы: логика и множества; математика в историческом развитии, что связанно с реализацией целей общекультурного развития обучающихся.

Содержание линии «Логика и множества»служит цели овладения обучающимися некоторыми элементами универсального математического языка.

Содержание линии «Математика в историческом развитии» способствует созданию общекультурного, гуманитарного фона изучения курса.

Содержание линии «Арифметика» служит базой для дальнейшего изучения обучающимися математики и смежных дисциплин, способствует развитию не только вычислительных навыков, но и логического мышления, формированию умения пользоваться алгоритмами, способствует развитию умений планировать и осуществлять деятельность, направленную на решение задач, а также приобретению практических навыков, необходимых в повседневной жизни. Развитие понятия о числе в основной школе связано с рациональными и иррациональными числами, формированием первичных представлений о действительном числе.

Содержание линии «Алгебра» способствует формированию у обучающихся математического аппарата для решения задач из разделов математики, смежных предметов и окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей процессов и явлений реального мира.

Развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики, и овладение навыками дедуктивного рассуждений также являются задачами изучения алгебры. Преобразование символьных форм вносит специфический вклад в развитие воображения обучающихся, их способностей к математическому творчеству. В основной школе материал группируется вокруг рациональных выражений.

Содержание раздела «Функции» нацелено на получение школьниками конкретных знаний о функции как важнейшей математической модели для описания и исследования разнообразных процессов. Изучение этого материала способствует развитию у обучающихся умения использовать различные языки математики (словесный, символический, графический), вносит вклад в формирование представлений о роли математики в развитии цивилизации и культуры.

Линия «Вероятность и статистика» - обязательный компонент школьного образования, усиливающий его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования у обучающихся функциональной грамотности – умения воспринимать и критически анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчеты. Изучение основ комбинаторики позволит обучающим осуществлять рассмотрение случаев, перебор и подсчет числа вариантов, в том числе в простейших прикладных задачах.

Образовательно-развивающие цели: развитие вычислительных и формально-оперативных алгебраических умений до уровня, позволяющего уверенно использовать их при решении задач математики и смежных предметов (физика, химия, основы информатики и вычислительной техники и др.), усвоение аппарата уравнений как основного средства математического моделирования прикладных задач, осуществление функциональной подготовки школьников, овладение приемами вычислений на калькуляторе.

Воспитательные цели: формирование представлений о математике как части общечеловеческой культуры, понимания значимости математики для общественного прогресса.

Контроль результатов  обучения   осуществляется  через использование  различных форм оценки и  контроля ЗУН: контрольная работа, самостоятельная работа, математический диктант, тест,  устный опрос. 

Место учебного предмета «Математика»  в учебном плане

Базисный учебный (образовательный) план на изучение алгебры в 7 классе основной школы отводится 3 часа в неделю, всего 102 часа.

Результаты изучения учебного предмета

Программа обеспечивает достижение следующих результатов освоения образовательной программы основного общего образования:

Личностные:

•       сформированность ответственного отношения к учению, готовность и способности обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию, выбору дальнейшего образования на базе ориентировки в мире профессий и профессиональных предпочтений, осознанному построению индивидуальной образовательной траектории с учетом устойчивых познавательных интересов;

сформированность целостного мировоззрения, соответствующего современному уровню развития науки и общественной практики;

сформированность коммуникативной компетентности в общении и сотрудничестве со сверстниками, старшими и младшими, в образовательной, общественно полезной, учебно-исследовательской, творческой и других видов деятельности;

умения ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;

•       представление о математической науке как сфере человеческой деятельности, об этапах ее развития, о ее значимости для развития цивилизации;

•       критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;

•       креативность мышления, инициатива, находчивость, активность при решении алгебраических задач;

•       умение контролировать процесс и результат учебной математической деятельности;

•       способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений.

Метапредметным результатом изучения курса является формирование универсальных учебных действий (УУД). 

Регулятивные:

•       принимать учебную задачу и следовать инструкции учителя;

•       планировать свои действия в соответствии с учебными задачами и инструкцией учителя;

•       выполнять действия в устной форме;

•       учитывать выделенные учителем   ориентиры   действия в учебном материале;

•       в сотрудничестве с учителем находить несколько вариантов решения учебной задачи,   представленной на наглядно-образном уровне;

•       вносить необходимые коррективы в действия на основе принятых правил;

•       выполнять учебные действия в устной и письменной речи;

•       принимать установленные правила  в  планировании  и контроле способа решения;

•       осуществлять  пошаговый контроль  под руководством учителя в доступных видах учебно-познавательной   деятельности;       понимать смысл инструкции учителя и заданий, предложенных в учебнике;

•       выполнять действия в опоре на заданный ориентир;

•       воспринимать мнение и предложения (о способе решения задачи) сверстников;

•       в сотрудничестве с учителем, классом находить несколько вариантов решения учебной задачи;

•       на основе вариантов решения практических задач под руководством учителя делать выводы о свойствах изучаемых объектов;

•       выполнять учебные действия в устной, письменной речи и во внутреннем плане;

•       самостоятельно оценивать правильность выполнения действия и вносить необходимые коррективы в действия с наглядно-образным материалом.

Познавательные:

•       осуществлять поиск нужной информации, используя материал учебника и сведения, полученные от взрослых;

•       использовать рисуночные и символические варианты математической записи; кодировать информацию в знаково-символической форме;       на основе кодирования строить несложные модели математических понятий, задачных ситуаций;

•       строить небольшие математические сообщения в устной форме;

•       проводить сравнение (по одному или нескольким основаниям, наглядное и по представлению, сопоставление и противопоставление), понимать выводы, сделанные на основе сравнения;

выделять в явлениях существенные и несущественные, необходимые и достаточные признаки; проводить аналогию и на ее основе строить выводы;

в сотрудничестве с учителем проводить классификацию изучаемых объектов; строить простые индуктивные и дедуктивные рассуждения;

под руководством учителя осуществлять поиск необходимой и дополнительной информации; работать с дополнительными текстами и заданиями;

•       соотносить содержание схематических изображений с математической записью;

•       моделировать задачи на основе анализа жизненных сюжетов;

•       устанавливать  аналогии; формулировать выводы на основе аналогии, сравнения, обобщения;

•       строить рассуждения о математических явлениях;

•       пользоваться эвристическими приемами для нахождения решения математических задач.

Коммуникативные:

•       принимать активное участие в работе парами и группами, используя речевые коммуникативные средства;          допускать  существование различных точек зрения;

•       стремиться к координации различных мнений о математических явлениях в сотрудничестве; договариваться, приходить к общему решению;     использовать в общении правила вежливости;

•       использовать простые речевые  средства для  передачи своего мнения;

•       контролировать свои действия в коллективной работе;

•       понимать содержание вопросов и воспроизводить вопросы;

•       следить за действиями других участников в процессе коллективной познавательной деятельности.

•       строить понятные для партнера высказывания и аргументировать свою позицию;

•       использовать средства устного общения для решения коммуникативных задач;

•       корректно формулировать свою точку зрения;

•       проявлять инициативу в учебно-познавательной деятельности;     контролировать свои действия в коллективной работе;          осуществлять взаимный контроль.

Предметным результатом изучения курса является сформированность следующих умений.

Дроби и проценты

•       Сравнивать дроби;

•       Правило перекрестного сравнения обыкновенных дробей;

•       Выполнять вычисления с рациональными числами;

•       Вычислять выражения с натуральными показателями;

•       Знать что такое основание и показатель степени;

•       Решать задачи на проценты;

•       Находить среднее арифметическое, моду и размах числового ряда;          Применять полученные знания при решении задач.

Прямая и обратная пропорциональность

Осуществлять перевод задач на язык формул;

Выполнять числовые подстановки в формулы;

Выражать переменные из формул;

Знать прямо пропорциональные выражения, обратно пропорциональные;

Знать формулу обратной пропорциональности;

Решать задачи с помощью пропорций;

           Применять полученные знания при решении задач.

Введение в алгебру

•       Знать основные свойства сложения и умножения чисел;

•       Применять основные свойства сложения и умножения при решении примеров;

•       Преобразовывать буквенные выражения;

•       Знать правила раскрытия скобок;

•       Приводить подобные слагаемые;

•       Применять полученные знания при решении задач.

Уравнения

•       Решать задачиалгебраическим способом;

•       Находить корни уравнения;

•       Решать задачи с помощью уравнений;

•       Применять полученные знания при решении задач.

Координаты и графики

•       Отмечать множество точек на координатной прямой;

•       Находить расстояние между точками координатной прямой;

•       Отмечать точек на координатной плоскости;

•       Знать что такое графики;

•       Изображать графики;

•       Применять полученные знания при решении задач.

Свойства степени с натуральным показателем

•       Находить произведение и частное степеней;

•       Решать комбинаторных задач;

•       Использовать правило перестановки при решении задач;  Применять полученные знания при решении задач.

Многочлены 

•       Знать определения одночленов и многочленов;

•       Выполнять действия с одночленами и многочленами;

•       Использовать формулы квадрата суммы и квадрата разности при выполнении заданий;  Решение задач с помощью уравнений.

Разложение многочленов на множители Выносить общий множитель за скобки;

Использовать способ группировки;

Использовать формулу разности квадратов, формулы разности и суммы кубов; Раскладывать на множители с применением нескольких способов; Решать уравнения с помощью разложения на множители.

Частота и вероятность

                           Вычислять относительную частоту случайного события.

Содержание программы

Дроби и проценты Сравнение дробей. Вычисления с рациональными числами. Степень с натуральным показателем. Задачи на проценты. Статистические характеристики. 

Прямая и обратная пропорциональность Зависимости и формулы. Прямая пропорциональность. Обратная пропорциональность. Пропорции. Решение задач с помощью пропорций. Пропорциональное деление.

Введение в алгебру Буквенная запись свойств действий над числами. Преобразование буквенных выражений. Раскрытие скобок. Приведение подобных слагаемых.

Уравнения Алгебраический способ решения задач. Корни уравнения. Решение уравнений. Решение задач с помощью уравнений.

Координаты и графики Множества точек на координатной прямой. Расстояние между точками координатной прямой. Множества точек на координатной плоскости. Графики. Еще несколько важных графиков. Графики вокруг нас.

Свойства степени с натуральным показателем Произведение и частное степеней. Степень степени, произведения и дроби. Решение комбинаторных задач. Перестановки.

Многочлены Одночлены и многочлены. Сложение и вычитание многочленов. Умножение одночлена на многочлен. Умножение многочлена на многочлен. Формулы квадрата суммы и квадрата разности. Решение задач с помощью уравнений.

Разложение многочленов на множители Вынесение общего множителя за скобки. Способ группировки. Формула разности квадратов. Формулы разности и суммы кубов. Разложение на множители с применением нескольких способов. Решение уравнений с помощью разложения на множители. Частота и вероятность Случайные события. Частота случайного события. Вероятность случайного события. Повторение 

Система оценивания

Рекомендации по оценке знаний, умений и навыков учащихся по математике:

Опираясь на эти рекомендации, учитель оценивает знания, умения и навыки учащихся с учетом их индивидуальных особенностей.

1.                   Содержание и объем материала, подлежащего проверке, определяется программой. При проверке усвоения материала нужно выявлять полноту, прочность усвоения учащимися теории и умения применять ее на практике в знакомых и незнакомых ситуациях.

2.                   Основными формами проверки знаний и умений, учащихся по математике являются письменная контрольная работа и устный опрос.

3.                   Среди погрешностей выделяются ошибки и недочеты.

    Погрешность считается ошибкой, если она свидетельствует о том, что ученик не овладел основными знаниями, умениями, указанными в программе.

    К недочетам относятся погрешности, свидетельствующие о недостаточно полном или недостаточно прочном усвоении основных знаний и умений или об отсутствии знаний, которые  в программе не считаются основными. Недочетами также считаются: погрешности, которые не привели к искажению смысла полученного учеником задания или способа его выполнения: неаккуратная запись, небрежное выполнение чертежа.

4.                   Задания для устного и письменного опроса учащихся состоят из теоретических вопросов и задач.

       Ответ на теоретический вопрос считается безупречным, если по своему содержанию полностью соответствует вопросу, содержит все необходимые теоретические факты  и обоснованные выводы, а его изложение и письменная запись математически грамотны и отличаются последовательностью и аккуратностью.

Решение задачи считается безупречным, если правильно выбран способ решения, само решение сопровождается необходимыми объяснениями, верно, выполнены нужные вычисления и преобразования, получен верный ответ, последовательно и аккуратно записано решение.

5.                   Оценка ответа учащихся при устном и письменном опросе производится по пятибалльной системе.

6.                   Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии учащегося, за решение более сложной задачи или ответ на более сложный вопрос, предложенные учащемуся дополнительно после выполнения им задания.

7.                   Итоговые отметки (за тему, четверть, курс) выставляются по состоянию знаний на конец этапа обучения   с учетом текущих отметок.

Оценка устных ответов учащихся. Ответ оценивается отметкой «5», если ученик:

•     полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;

•     изложил материал грамотным языком в определенной логической последовательности, точно используя математическую терминологию и символику;  правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;

•     показал умение иллюстрировать теоретические положения конкретными примерами, применять их в новой ситуации при выполнении практического задания;  продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность и устойчивость использованных при ответе умений и навыков;  отвечал самостоятельно без наводящих вопросов учителя.

Возможны одна – две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил по замечанию учителя.

Ответ оценивается отметкой «4»,если он удовлетворен в основном требованиям на отметку «5», но при этом имеет один из недостатков:

•     в изложении допущены небольшие пробелы, не исказившие математического содержания ответа, исправленные по замечанию учителя.

•     допущены ошибки или более двух недочетов при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил по замечанию учителя. Отметка «3»  ставится в следующих случаях:

•     неполно или непоследовательно раскрыто содержание материала, но показано общее понимание вопроса и продемонстрированы умения, достаточные для дальнейшего усвоения программного материала (определенные «Требованиями к математической подготовке учащихся»).

•     имелись затруднения или допущены ошибки в определении понятий и, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;

•     ученик не справился  с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;

•     при знании теоретического материала выявлена недостаточная сформированность умений и навыков.

Отметка «2»  ставится в следующих случаях:

•     не раскрыто основное содержание учебного материала;

•     обнаружено незнание или непонимание учеником большей или наиболее важной части учебного материала;

•     допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

Оценка «1» ставится в случае, если:

•     ученик обнаружил полное незнание  и непонимание изучаемого материала или не смог ответить ни на один из поставленных вопросов по изучаемому материалу.

Оценка письменных работ учащихся. Отметка «5»  ставится в следующих случаях:

•     работа выполнена полностью.

•     в логических рассуждениях и обоснованиях нет пробелов и ошибок;

•     в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала); Отметка «4» ставится, если:

•     работа выполнена полностью, но обоснования шагов решения недостаточны (если умения обосновывать рассуждения не являлись специальным объектом проверки);

•     допущена одна ошибка или два-три недочета в выкладках, чертежах или графиках (если эти виды работы не являлись специальным объектом проверки); Отметка «3» ставится, если:

•     допущены более одной ошибки или более двух- трех недочетов в выкладках, чертежах или графика, но учащийся владеет обязательными умениями по проверяемой теме.

Отметка «2» ставится, если:

•     допущены существенные ошибки, показавшие, что учащийся не владеет обязательными знаниями по данной теме в полной мере. Отметка «1» ставится, если:

•     работа показала полное отсутствие у учащегося обязательных знаний, умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.

Перечень контрольных работ, 7 класс

1.                  Контрольная работа №1 по теме «Дроби и проценты»

2.                  Контрольная работа №2 по теме «Прямая и обратная пропорциональность»

3.                  Контрольная работа №3 по теме «Введение в алгебру»

4.                  Контрольная работа №4 по теме «Уравнения»

5.                  Контрольная работа №5 по теме «Координаты  и графики»

6.                  Контрольная работа №6 по теме «Свойства степени с натуральным показателем»

7.                  Контрольная работа №7 по теме «Одночлены и многочлены»

8.                  Контрольная работа №8  по теме «Составление и решение уравнений»

9.                  Контрольная работа №9 по теме «Разложение многочлена на множители»

10.               Контрольная работа №10 по теме «Частота и вероятность»

11.               Контрольная работа №11 « Итоговая контрольная работа за курс 7 класса»

КРИТЕРИИ ОЦЕНИВАНИЯ Контрольная работа № 1. Т е м а : ДРОБИ И ПРОЦЕНТЫ

ЧЛЕНЫ

ПОРЦИОНАЛЬНОСТЬ

УРАВНЕНИЙ

НОВ НА МНОЖИТЕЛИ

Контрольная работа № 4. Т е м а : УРАВНЕНИЯ

Контрольная работа №  5. Т е м а : КООРДИНАТЫ И ГРАФИКИ Итоговая контрольная работа

С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ

Контрольные работы – 7 класс Входной срез. 7 класс. 

             а)  _             б) 3,2550,6                                                          а)        б) 2 :1,6

3.     Вычислите::3      3. Вычислите: 94,3:4,6 – 1,75 · 0,6

4.     Упростите выражение 6a7 4a1.

4.                     Найдите значение выражения 0,3a 7 приa5. 5. Определите, сколько человек на уроке физкуль-

5.                     В магазин привезли печенье. В первый день про- туры, если  присутствующих на уроке прыгают в длину, дали 52 кг печенья, а во второй день – в 1,3 раза меньше, чем в первый. Сколько килограммов печенья привезли в 25% прыгают в высоту, а остальные 7 человек играют в магазин, если за два дня продали  привезенного печенья? мяч.

Контрольные работы – 7 класс Входной срез. 7 класс. 

             а) _             б) 3,2550,6                                                           а)       б) 2 :1,6

3.              Вычислите::3   8. Вычислите: 94,3:4,6 – 1,75 · 0,6

9. Упростите выражение 6a7 4a1.

4.              Найдите значение выражения 0,3a 7 приa5. 10. Определите, сколько человек на уроке физкуль-

5.              В магазин привезли печенье. В первый день про- туры, если  присутствующих на уроке прыгают в длину, дали 52 кг печенья, а во второй день – в 1,3 раза меньше, чем в первый. Сколько килограммов печенья привезли в 25% прыгают в высоту, а остальные 7 человек играют в магазин, если за два дня продали  привезенного печенья? мяч.

11

Контрольная работа № 1.

В а р и а н т I О б я з а т е л ь н а я ч ас т ь .

                                                            6        5

1.                  Сравните числа: а) 11 и 9 ;    б)  и 0,25.

2.                  Выполните действия:

         а) 0,17 + ;                     б) 2,5 : .

3.                  Вычислите: . a b

4.                  Найдите значение выражения ac приа = –4, b = –6, с = 3.

5.                  Вычислите: 20 – 0,5 ∙  (–2)⁵.

6.                  Спортивный костюм до уценки товаров стоил 800 р. Сколько заплатит покупатель за этот костюм, если он продается со скидкой 7,5 %?

7.                  В течение недели семья отмечала ежедневный расход воды (в л) и получила следующие данные: 5,7; 6,5; 6,1; 6,5; 6,5; 6,8; 6,7.

Найдите среднее арифметическое и размах полученных данных.

Д о п о л н и т е л ь н а я ч а с т ь .

8.                  Расположите в порядке возрастания числа:

–0,2; (–0,2)²; (–0,2)³; (–0,2)⁴.

9.                  Фирма платит рекламным агентам 5 % от стоимости заказа. На какую сумму агент должен найти заказ, чтобы заработать 1 000

р.?

10.              В ряду чисел 8, 10, 14, 6, 12, 16 одно число вычеркнули. Среднее арифметическое нового ряда стало равно 12. Найдите вычеркнутое число.

В а р и а н т II О б я з ат е л ь н а я ч а с т ь .

                                                                                                                            4      4

1.                  Расположите в порядке возрастания числа: 0,5; 15 ; 11.

2.                  Выполните действия:

        а)   0,06;           б)  

3.                  Вычислите: 6,5 : 1,5 ∙  0,09.

ab

4.                  Найдите значение выражения a c приа = –5, b = 6, с = 7.

2 5³

^{ }

5.                  Вычислите: –72 ∙ ^{3 6} .

6.                  Зимой в зоопарке проживало 120 животных, а к лету их стало 150. На сколько процентов увеличилось число животных в зоопарке?

7.                  В течение полугода ежемесячный расход электроэнергии (в кВт ∙  ч) в семье был следующий: 148; 148; 125; 126; 112; 115.

Найдите среднее арифметическое и размах полученных данных.

Д о п о л н и т е л ь н а я ч а с т ь .

1а³

8.                  Найдите значение выражения 1а приа = –0,5.

9.                  После снижения цен на 20 % килограмм груш стал стоить 36

р. Сколько стоил килограмм груш до снижения цен?

10.              К ряду чисел 16, 12, 20, 18, 14 приписали еще одно число. Среднее арифметическое нового ряда стало равно 15. Какое число приписали?

Вариант I Обязательная часть.

1.     Площадь поверхности параллелепипеда можно вычислить по формуле S = 2 (ab + bc + ac). Найдите площадь поверхности параллелепипеда, если а = 4 см, b = 2,5 см, с = 6 см.

2.     Лыжники должны пройти а км. Они идут со скоростью v км/ч. Составьте формулу для вычисления расстояния S, которое останется пройти лыжникам через t ч.

3.     В бассейн начали подавать воду, и через некоторое время вода поднялась до уровня 30 см. До какого уровня поднялась бы вода за это же время, если бы скорость подачи воды была в 3 раза выше?

4.     Найдите      неизвестный        член ⁷ _ ^0,21

пропорции .                                                     ^{5          а}

5.     На каждые 100 км пути автомобиль расходует 9 л бензина. Сколько бензина потребуется, чтобы проехать 450 км?

Дополнительная часть .

6.     Даны три числа: 15, 6 и 5. Найдите четвертое число, чтобы из этих чисел можно было составить пропорцию. Найдите все решения задачи.

7.     Автомобиль проехал некоторое расстояние за 2,4 ч. За какое время он проедет это же расстояние, если уменьшит скорость на 20 %?

8.     Периметр  треугольника  равен  70  см.  Найдите  длины  сторон  этого  треугольника,  если  АВ  относится  к  ВС  как  3 : 4,  а  ВС  относится  к АС как 6 : 7.

Вариант II Обязательная часть.

1.                      Площадь  поверхности  цилиндра  можно  вычислить  по  формуле S = 2πr (r + h).  Найдите  площадь  поверхности  цилиндра,  если  r = 5 cм, h = 10 см (π ≈ 3,14).

2.                      Чашка чая и пирожок стоят соответственно а р. и b

р. Составьте формулу для вычисления оплаты С за m чашек чая и n пирожков.

3.                      Цех за 6 дней выполнил некоторый заказ на изготовление бетонных плиток для дорожек. За какое время такое же количество плиток изготовит другой цех, производительность которого в 2 раза ниже?

4.                      Найдите неизвестный член пропорции . ^х _ ⁷

                                                                                6      4,2

5.Распределите 450 тетрадей пропорционально числам

2 : 3 : 4.

Дополнительн ая часть.

                                                                                                                1       5

 6. Найдите неизвестное число х, если  ^{3х 0,3}.

7.     Скорость автомобиля на трассе оказалась на 50 % выше скорости этого автомобиля по городу. Какое время затрачивает автомобиль на трассе на преодоление расстояния, на которое в городе у него уходит 1,2 ч?

8.     Всего имеется 400 г семян. Их надо насыпать в три пакета так, чтобы масса семян в первом пакете составила 40 %,  а масса семян во втором пакете – 50 % массы семян в третьем пакете. Сколько семян будет в каждом пакете?

Контрольная работа № 3.

Вариант I Обязательная часть.

1.                Упростите произведение:

        а) 3ас∙  5аb;     б) 10х∙  9у ∙  (–7а).

2.                Приведите подобные слагаемые в сумме b – 6a – 10b + 9a + 4b.

3.                Составьте выражение по условию задачи.

В фермерском хозяйстве х гусей, уток в 2 раза больше, чем гусей, а кур на 20 больше, чем уток. Сколько всего птиц в фермерском хозяйстве? 4. Найдите значение выражения: bm + 2 – (5 + 7m) – 4m при m = 17.

5.     Упростите выражение 7 (у + 2х) – 2 (х – 2у).

Дополнительная часть .

6.     В выражение у – х – z подставьте х = аb + b, у = ab + c, z = ab – b и упростите получившееся выражение.

7.     Раскройте скобки в выражении: 2с – (3с + (2с – (с + 1)) + 3).

8.     У учителя 300 тетрадей. Ежедневно он раздает по 27 тетрадей. Сколько тетрадей останется через n дней? Какие значения может принимать число n?

Вариант II Обязательная часть.

1.                Упростите произведение:

        а) 6cd∙  2ac;     б) 4m∙  (–5n) ∙  (–8k).

2.                Приведите подобные слагаемые в сумме 4 – 12b – 2a + 5b – a.

3.                Составьте выражение по условию задачи.

В  первый  день  на  ярмарке  фермер  продал  хкг  овощей,  во  второй день – в 3 раза больше, в третий – на 150 кг меньше, чем в первый. Сколько килограммов овощей продал фермер за 3 дня? 4. Найдите значение выражения:

11n – (7n – 1) – 6n + 8   при n = 16.

5.   Упростите выражение: 4 (2а – c) – 5(а + 3c).

Дополнительная часть.

6.   В выражение у – х – 1 подставьте х = аb+ 1, у = ab –

1 и упростите получившееся выражение. 7. Упростите выражение: х (у + z) – y (x + z) – z (x – y).

8. Пусть сумма трех последовательных нечетных чисел равна В. Найдите сумму трех следующих нечетных чисел.

Контрольная работа №4

Вариант I Обязательная часть.

1. Является ли число (–1) корнем уравнения  х² – 4х – 5 = 0? Решите уравнение  2. 0,5х = –4,5.

3.      4 – 3х = 3.

4.      3х – 7 = х – 11.

5.      ^{х х}        = 10.

 2 3

6. Решите задачу с помощью уравнения.

Брат в 2 раза старше сестры. Сколько лет сестре и сколько брату, если им вместе 24 года?

Дополнительная часть.

11. Решите уравнение 10 – ((2х + 1) – х) = 3х.

8.     Выразите  из  равенства  3 (х – у) = –z  каждую  переменную  через другие.

9.     В классе 25 детей. При посадке деревьев в школьном саду каждая девочка посадила по 2 дерева, а каждый мальчик – 3 дерева. Всего было посажено 63 дерева. Сколько девочек в классе?

Контрольная работа №4

Вариант II Обязательная часть.

1.    Является ли число 5 корнем уравнения  х² – 2х – 5 = 0? Решите уравнение

               1

2.           x     = 2.

   ⁶

3.    5 + 2х = 0.

4.    2х + 6 = 3 + 5х.

5.    (х – 3) – (3х – 4) = 15.

6.    Решите задачу с помощью уравнения.

Масса изюма составляет 15 % массы фруктовой смеси. Сколько получится смеси, если взято 90 г изюма?

Дополнительная часть.

7.    Решите уравнение:      (7 – 2х) =        .

1                     8. Выразите  из  равенства  5 (у – 2х) =   z  каждую  пе-

2                     ременную  через другие.

9. В баке в 2 раза больше молока, чем в ведре. Если из бака перелить в ведро 2 л, то в баке будет на 5 л молока больше, чем в ведре. Сколько молока в ведре и сколько в баке?

Контрольная работа №5

Контрольная работа №  5. Т е м а : КООРДИНАТЫ И ГРАФИКИ

                      Оценка                    «Зачет»               «4»                   «5»

Обязательная часть                 4 задания        4 задания         5 заданий

Дополнительная часть                                   1 задание         2 задания

В а р и а н т I

О б я з а т е л ь н а я ч а с т ь .

1.      Изобразите на координатной прямой промежутки: 

        а) х ≥ 1;                 

б) –6 < х < – 2.

2.      Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют условию: 

а) х = –2; 

б) у = 4.

3.      Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют условию: 

        а)  у ≤ –1;              

б) –3 ≤  х  ≤ 1.

4.      Изобразите на координатной плоскости множество точек, удовлетворяющих условиям: 

у = –х и –5 ≤ х ≤ 5.

5.      На рисунке 5.55 в учебнике (с. 151) изображен график изменения температуры воздуха в течение одного дня. Используя график, ответьте на вопросы:

а) Какова была минимальная температура в этот день?

б) В какое время суток температура в этот день была равна 2 °С?

в) Когда в течение суток температура повышалась?

Д о п о л н и т е л ь н а я ч а с т ь .

6.      Найдите  пересечение  промежутков, заданных неравен-

ствами | x | ≤ 8 и –9 ≤ x ≤ 2

7.      Изобразите на координатной плоскости множество точек, удовлетворяющих условиям у = х³ и | x | ≤ 4.

8.      Прямоугольник задан неравенствами –1 ≤ х ≤  и  1 ≤ у ≤ 3. Задайте неравенствами другой прямоугольник, симметричный данному относительно оси абсцисс.

Контрольная работа №5

Контрольная работа №  5. Т е м а : КООРДИНАТЫ И ГРАФИКИ

                      Оценка                    «Зачет»               «4»                   «5»

Обязательная часть                 4 задания        4 задания         5 заданий

Дополнительная часть                                   1 задание         2 задания

В а р и а н т II

О б я з а т е л ь н а я ч а с т ь .

1.      Изобразите на координатной прямой промежутки: 

        а) х≤ –2;                

б) 0 < х < 5.

2.      Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют условию:

        а) х = 5;                 

б) у = –3.

3.      Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют условию: 

        а)  х ≥ 4;                

б) 0 ≤  у  ≤ 5

4.      Изобразите на координатной плоскости множество точек, удовлетворяющих условиям:

у = х; и –3 ≤ х ≤ 3.

5.      На рисунке 5.56 из учебника (с. 152) изображен график движения туриста от туристического лагеря до станции. Используя график, ответьте на вопросы:

а) Сколько километров прошел турист за последний час пути?

б) Сколько километров прошел турист до привала?

в) За какое время турист отошел от лагеря на 5 км?

Д о п о л н и т е л ь н а я ч а с т ь .

6.      Найдите  пересечение  промежутков, заданных неравенствами

| x | ≤ 5 и –7 ≤ x ≤ 1.

7.      Постройте график зависимости:

x при x 0, y^ ² x 0. x при

8. Опишите  на  алгебраическом  языке  множество  точек,  симметричных  относительно  оси  ординат  точкам  полосы,  заданной  неравенством 2 ≤ x ≤ 6.

Контрольная работа №6.

Вариант I Обязательная часть.

Выполните действие, воспользовавшись соответствующим свойством степени (1–5).

1. х²∙ х⁸.  2. а⁹ :а³.  3. (сⁿ)³.  4. (ху)².

 b ⁿ

5.   c .

Упростите выражение (6–9).

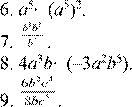
10.                        В финал конкурса вышли пять его участников. Сколькими способами могут распределиться два первых места?

Дополнительная часть .

с2k5

11.                        Представьте выражение c c^{k } в виде степени с основанием с.

12.                        При каком значении n выполняется равенство (3^{n – 1})² = 81? 13. Сравните: 121²⁰ и 3²⁰∙  5²⁰.

Вариант II

Обязательная часть

Выполните действие, воспользовавшись соответствующим свойством степени (1–5).

1. с⁹∙ с².  2. b⁸ :b⁴.  3. (а⁵)³.  4. (ху)ⁿ.

 b ³

5.   c .

Упростите выражение (6–9).

.

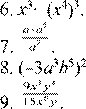10.                        Сколько четырехзначных чисел, в записи которых все цифры различны, можно составить из цифр 1, 2, 3, 4?

Дополнительная часть .

сk5 ck

11.                        Представьте выражение ^{( )c2 k} в виде степени с основанием с.

12.                        При каком значении n выполняется равенство 10^{2 (n – 1)} = 10 000.

13.                        Сравните: 55⁸ и 11¹⁶.

Контрольная работа №7.

О б я з а т е л ь н а я ч а с т ь .

1.      Найдите значение выражения 1,5х³ – 2,4у при х = –1, у = 2. Представьте в виде многочлена (2–4).

2.      –4х³ (х² – 3х + 2).

3.      (1 – х) (2у + х).

4.      (5с – 4)². Упростите выражение (5–6).

5.      3а (а – b) + (b (2a – b).

6.      3с (с – 2) – (с – 3)².

7.      Представьте в виде квадрата двучлена выражение  9 + 12х + 4х².

Д о п о л н и т е л ь н а я ч а с т ь .

8.      Упростите выражение:

(3х + 1) (4х – 2) – 6 (2х – 1)² + 14.

                                               (а²  1)²  (а² 1)²

9.      Докажите, что а       = 4.

                                                                                          1              1        а

2

10.  Найдите значение выражения а² + с , если а – с = 2, с = 3.

В а р и а н т II О б я з а т е л ь н а я ч а с т ь .

1.  Найдите значение выражения 2х² – 0,5у + 6 при х = 4, у = –2. Представьте в виде многочлена (2–4).

2.  5а² (4а³ – а² + 1).

3.  (3с – х) (2с – 5х).

4.  (3а + 2b)². Упростите выражение (5–6).

5.  5х (2х + 3) – (х – 1) (х – 6).

6.  (а – с)² – с (а – 3с).

7.  Представьте в виде квадрата двучлена выражение  4а² – 20ах + 25х².

Д о п о л н и т е л ь н а я ч а с т ь .

8.  Докажите, что если х – у – z = 0, то х (уz + 1) – y (xz + 1) – z (xy + 1) =

= –xyz. 9. Выполните возведение в квадрат: (3а² + 1 – а)².

10. Найдите значение выражения а² + b², если а – b = 6, ab = 10.

Контрольная работа №8. О б я з а т е л ь н а я ч а с т ь .

1.Лодка проплыла расстояние между пристанями вниз по течению реки и вернулась обратно, затратив на весь путь 5 ч. Собственная скорость лодки равна 10 км/ч, а скорость течения реки – 2 км/ч. Сколько времени лодка плыла по течению реки?

Составьте уравнение по условию задачи, обозначив через х время, которое лодка плыла по течению реки.

2.По условию предыдущей задачи составьте уравнение, обозначив через х расстояние между пристанями. Решите уравнение (3–4).

3.7 – 3 (х – 1) = 2х.

4.6 (2х + 0,5) = 8х – (3х + 4).

5.Площадь прямоугольника на 15 см² меньше площади квадрата. Одна из сторон прямоугольника равна стороне квадрата, а другая на 3 см меньше ее. Найдите сторону квадрата.

Д о п о л н и т е л ь н а я ч а с т ь .

Решите уравнение (6–7).

6.(х + 4)² = х (х + 3).

7.10 – х (5 – (6 + х)) = х (х + 3) – 4х.

8.Фабрика предполагала выпустить партию изделий за 36 дней. Однако она выпускала ежедневно на 4 изделия больше, поэтому за 8 дней до срока ей осталось выпустить 48 изделий. Сколько изделий в день предполагалось выпускать первоначально?

В а р и а н т II О б я з а т е л ь н а я ч а с т ь .

1.Из двух пунктов, расстояние между которыми равно 245 км, одновременно навстречу друг другу выехали автобус и автомобиль. Они встретились через 2 ч. С какой скоростью ехал каждый из них, если известно, что скорость автомобиля на 15 км/ч больше скорости автобуса?

Составьте уравнение по условию задачи, обозначив через х скорость автобуса (в км/ч).

2.По условию предыдущей задачи составьте уравнение, обозначив через х скорость автомобиля (в км/ч). Решите уравнение (3–4).

3.5х – 2 (х – 3) = 6х.

4.6х – (2х + 5) = 2 (3х – 6).

5.Площадь прямоугольника равна площади квадрата. Одна из сторон прямоугольника на 4 см больше стороны квадрата, а другая – на 3 см меньше ее. Найдите сторону квадрата.

Д о п о л н и т е л ь н а я ч а с т ь .

Решите уравнение (6–7).

6.х (х + 5) = (х + 3)².

7.х (х (х – 1)) + 6 = х (х + 3) (х – 4).

8.Фабрика должна выпустить партию изделий за 10 дней. Но оказалось, что надо выпустить на 70 изделий больше. Поэтому ежедневно выпускали на 3 изделия больше, чем предполагалось, и работа продолжалась на 2 дня дольше. Сколько изделий в день предполагалось выпускать первоначально?

Контрольная работа №9.

О б я з а т е л ь н а я ч ас т ь .

Вынесите общий множитель за скобки (1–2).

1. 3а³b – 12a²b + 6ab. 2. х (х – 1) + 2 (х – 1).

Разложите на множители (3–5).

3.  ху + 3у + xz + 3z.

4.  25 – с².

5.  аb² – 2abc + ac².

х²  ху

6.  Сократите дробь ^{х2  у2} .

7.  Выполните действия: (а – 2) (а + 2) – а (а – 1). Решите уравнение (8–9).

8.  (2х + 8)² = 0.

9.  х² – 4х = 0.

Д о п о л н и т е л ь н а я ч а с т ь .

10.  Представьте (а + b) (a – b) (a² + b²) в виде многочлена. 11. Упростите выражение: с (с – 2) (с + 2) – (с – 1) (с² + с + 1). 12. Разложите на множители: 2х + 2у– х² – 2ху – у².

В а р и а н т II О б я з ат е л ь н а я ч а с т ь .

Вынесите общий множитель за скобки (1–2).

1.      16а⁴ – 4а³ + 8а².

2.      7 (х – 2) – х (х – 2).

Разложите на множители (3–5).

3.      5а – аb + 5c – cb.

4.      9а² – с².

5.      2b² – 12bc + 18c².

х² 4х

6.      Сократите дробь х² 16 .

7.      Выполните действия: 2с (с – b) – (c – 3) (c + 3). Решите уравнение (8–9).

8.      (х – 1) (2х + 6) = 0.

9.      х² – 16 = 0.

Д о п о л н и т е л ь н а я ч а с т ь .

10.  Представьте (а + b)² – (a² – b²) в виде произведения.

11.  Разложите на множители: а⁴b + ab⁴.

12.  Решите уравнение (1 – 3х)² + 3х – 1 = 0.

Контрольная работа № 10. Частота и вероятность

Вариант 1

Обязательная часть

1.      Спортсмен сделал 40 выстрелов и попал в мишень 32 раза. Определите относительную частоту попаданий.

2. 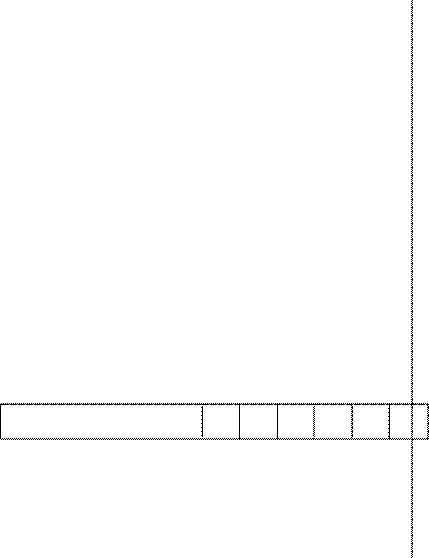     В отделе контроля завода проверили 500 деталей и у 75 из них обнаружили брак. На вероятностной шкале отметьте вероятность появления бракованной детали.

3.      Фермеру известно, что вероятность получения качественных кочанов капусты составляет 0,85. Сколько предполагается собрать кочанов капусты, если высажено 200 кустов ее рассады?

Дополнительная часть

4. В школе 300 учащихся. Известно, что за неделю было 40 опозданий к первому уроку. Случайным образом выбрали одного ученика. Какова вероятность того, что у него не было опозданий?

Количество выпавших оч-  1          2          3          4          5          6 ков Число наступлений события 33             57        65        45        64        36

5.    Игральный кубик подбросили 300 раз. Результаты эксперимента занесли в таблицу.

                          Количество выпавших очков     1        2        3        4        5           6

                          Число наступлений события      33      57      65      45      64       36

Какова частота наступления события «выпало не более двух очков»?

6.    Случайным образом выбирают два последовательных натуральных числа, меньшие 10. Какова вероятность события «сумма выбранных чисел равна 20»?

Вариант 2

Обязательная часть

1.    Во время 60 подбрасываний монеты орел выпал 24 раза. Определите относительную частоту выпадения орла.

2.    Выпущено 1000 лотерейных билетов, среди которых 50 билетов выигрышные. На вероятностной шкале отметьте вероятность появления выигрышного билета.

3.    В некоторой школе вероятность опозданий учащихся к началу уроков по понедельникам составила 0,05. Сколько примерно опоздавших в такой день окажется среди 600 учащихся?

Дополнительная часть

4.    При проверке партии приборов оказалось, что на каждые 400 приборов приходится 6 бракованных. Какова вероятность того, что взятый наугад прибор из этой партии будет без брака?

5.    Игральный кубик подбросили 300 раз. Результаты эксперимента занесли в таблицу.

Какова частота наступления события «выпало не менее пяти очков»?

6.    Случайным образом выбирают два последовательных натуральных числа, меньшие 10. Какова вероятность события «сумма выбранных чисел меньше 20»?

Итоговая контрольная работа  Вариант 1.

1.   Вычислите:  а)  2¹⁰∙(2²)²;    б)  0,4⁴∙25⁴; в)2¹¹

2.   Упростите выражение: (а - 2)(а + 3) – 2а (а - 4)

3.   Решите уравнение: (х - 2)( 3х +5)=0

4.   Сократите дробь:

5.   Изобразите на координатной плоскости множество точек, удовлетворяющих условиям   х и   у ≤ 3.

6.   Решите задачу: Катер, проплыв 158 км, плыл 1,5 ч по течению реки и 2,5 ч против течения. Скорость течения реки 2 км/ч. Вычислите собственную скорость катера и расстояние, которое он проплыл по течению реки.

Вариант 2.

1.   Вычислите: а)  3⁵ ∙ 3⁶ ;      б) 0,125⁶ ∙ 8⁶;  в) (3³)³

2.   Упростите выражение: 5m(m- 2) – (m+ 2)(m- 3)

3.   Решите уравнение: (5x - 7)(x + 3)=0

4.   Сократите дробь:

5.   Изобразите на координатной плоскости множество точек, удовлетворяющих условиям    х  ≤  3       и       y  ≤  4. 6. Решите задачу: Первый участок пути мотоциклист ехал со скоростью 38 км/ч, а второй – со скоростью 32км/ч. Всего он проехал 191 км. За сколько времени мотоциклист проехал первый участок пути и за сколько второй, если на первый участок он затратил на  ч    меньше, чем на второй?

Материально-техническое обеспечение учебного предмета.

Основная литература:

1.       Бурмистрова Т.А. Алгебра: сборник рабочих программ 7 – 9 классы. М.: «Просвещение», 2014;

2.       Дорофеев Г.В, Шарыгин И.Ф. Алгебра. 7 класс: учебник для общеобразовательных учреждений. М.: «Просвещение», 2017.

  Дополнительная литература: 

1  . Евстафьева Л.П. Алгебра: дидактические материалы для 7 класса общеобразовательных учреждений. М.: «Просвещение», 2017.

2  . Кузнецова Л.В. Алгебра: тематические тесты: 7 класс. М: «Просвещение», 2016

3  . Минаева С.С.Алгебра: рабочая тетрадь для 7 класса общеобразовательных учреждений. М.: «Просвещение», 2014;

40