Рабочий лист по теме «Маркетинг, торговля» (задачи и решения задач)

ЗАДАЧНИК ПО ЭКОНОМИКЕ

«МАРКЕТИНГ, ТОРГОВЛЯ»

(ЗАДАЧИ И РЕШЕНИЯ ЗАДАЧ)

 

 

 

 

 

 

 

 

 

 

 

 

 

ОТВЕТ:

Вначале рассчитаем процент и вес сухого остатка в товаре. При первом замере жидкости сухой остаток составил 1% и весил 1 т. При втором замере – соответственно 4% и снова 1 т (вес сухого остатка не меняется).

Интересующий нас вес всего товара (100%) при втором замере (Х) находм из очевидной пропорции:

4% - 1 т

100% - Х

Откуда Х = 25 т

За этот товар следует заплатить 25 т  300 тыс.д.ед. = 7,5 млн.д.ед.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рис. 1

 

ОТВЕТ:

Задача допускает несколько решений. Одно из наиболее интересных следующее. Фирма Б заключает с фирмой В контракт на поставку лишь половины товара, получаемого от фирмы А. тогда сумма этого контракта будет 100 млн.руб. и неустойка фирме В составит лишь 10 млн.руб. В случае, если фирма А сорвет контракт, фирма Б ничего не потеряет, выплачивая фирме В только то, что получит от фирмы А. Если же фирма А сделает нормальную поставку, фирма Б заключит с фирмой В контракт и на вторую половину товара.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ОТВЕТ:

Представим произведенные в условии задачи цифры, а также получающуюся при этом выручку (произведение количества проданных билетов на цену билета) в виде таблицы:

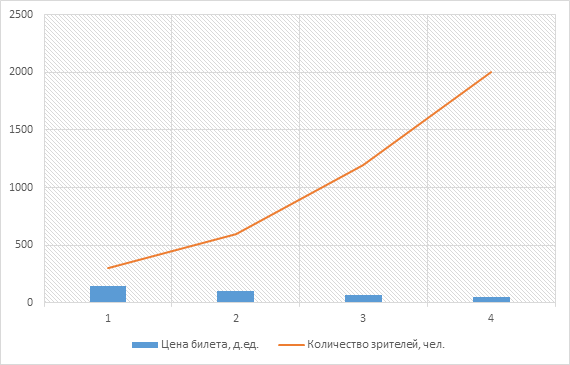
Из таблицы видно, что с уменьшением цены билета количество зрителей растет и выручка тоже растет.

Построим график зависимости количества зрителей от цены билета. Экстраполируя по графику (в предположении его главного характера), получаем, что предельная вместимость зала - 2000 человек – соответствует цене билета 50 д.ед.

Именно при этом обеспечивается выручка:

2000  50 д.ед. = 100 тыс.д.ед.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ОТВЕТ:

Зададимся следующими вопросами:

- за сколько дней Иванов израсходует 10 бочек?

10  14 = 140 дней

- сколько бочек  за эти же 140 дней израсходовали бы Иванов и Петров совместно?

 = 14 бочек

- сколько бочек за эти 14 дней израсходовал бы Петров?

14 – 10 = 4 бочки

- за сколько дней Петров израсходовал бы одну бочку?

 = 35 дней.

 

 

 

 

 

 

 

 

 

 

ОТВЕТ:

 

Во-первых, товар-предмет имеет материальный характер: его можно увидеть, пощупать, взвесить и т.п. Во-вторых, товар-предмет при купле-продаже передается от продавца покупателю. Товар же в форме услуги и после продажи остается у продавца, возможно его тиражирование и многократная продажа.

 

 

 

 

 

ОТВЕТ:

1) Ускорение оборота

2) Повышение цены товара за счет дополнительных услуг, сервиса

3) Повышение цены товара при предоставлении его в широком ассортименте

4) Повышение цены товара за предоставление его в комплекте с другими

5) Повышение цены товара за предоставление его весте с сопутствующими товарами

6) повышение цены товара за счет продажи его в удобное или необходимое для покупателя время

7) повышение цены товара за счет его новизны, временного отсутствия подобных товаров на рынке

8) повышение цены товара за счет риска выхода с данным товаром на рынок, на что конкурент не решился.

 

 

 

 

 

 

 

 

 

 

 

ОТВЕТ:

Нужда – это нехватка определенного круга предметов или услуг (например, нужда в пище, одежде, квалифицированной медицинской помощи).

Потребность – это нужда в конкретном товаре.

Спрос – это потребность, подкрепленная возможностью покупателя заплатить за товар.

 

 

 

 

 

 

 

 

ОТВЕТ:

При обмене вещами у совершающих обмен ничего существенно не меняется: скажем, было до обмена по яблоку и осталось после обмена по яблоку.

При обмене идеями у каждого было до обмена по одной идее, а в результате обмена стало две (т.е. в два раза больше).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ОТВЕТ:

В предвкушении еды нас интересует не величина яблока, а его объем. Отношение объемов шаров пропорционально отношению кубов их радиусов. В нашей задаче это отношение равно:

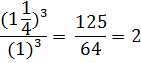
Следовательно, по объему первое яблоко больше второго примерно в 2 раза. А стоит оно всего в 1,5 раза дороже. Значит, такое яблоко покупать выгоднее.

 

 

 

 

 

 

 

ОТВЕТ:

Руководствуясь теми же соображениями, что и в решении задачи 9, составим соотношение объемов яиц:

Следовательно, второе яйцо выгоднее.

Уместно отметить, что соображения, высказанные при решении двух последних задач, справедливы по отношению к любым фруктам или овощам шарообразной, или близкой к ней формы: чем они крупнее, тем выгоднее.

 

 

 

 

 

 

ОТВЕТ:

 

Для решения задачи вообразим, что диаметр крупинок муки крупного помола больше, чем мелкого, скажем, в 10 раз. Увеличим мысленно крупинки мелкой муки до размера крупинок крупной. Одновременно увеличим во столько же раз и размер мешка. Тогда объем его вырастет в 10 10 10  раз. Во столько же раз увеличится и вес муки. И если мы теперь отсыплем из этого огромного мешка один наш мешок, то он составит одну тысячную веса большого мешка. Но ведь это и будет таким же, как и у мешка муки мелкого помола.

Следовательно, одинаковые по объему мешки муки мелкого и крупного помола равны и по весу.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ОТВЕТ:

1) Если на все деньги купить только радиоаппаратуру, то ее окажется 480 тыс.д.ед. : 30 тыс.д.ед. = 16 единиц. Но при этом экспедитор нарушает задание – купить товары всех трех видов. Поэтому ему придется ограничится 15-ю единицами радиоаппаратуры, оставив деньги на более мелкие покупки (одежду и бытовую технику).

2) Допустим, мелкие покупки уже сделаны. Тогда, если бы радиоаппаратура стоила по 10 тыс.д.ед. (менее 200 тыс.д.ед.), и осталось бы явно более 280 тыс.д.ед. (480 – 200) на доплату стоимость радиоаппаратуры – по 20 тыс.д.ед. (30 – 10) за каждую единицу. Следовательно, куплено было бы более 14 единиц (280 тыс.д.ед. : 20 тыс.д.ед.). итак, можно купить радиоаппаратуры не более 15 единиц, но более 14, т.е. 15 единиц.

За 15 единиц радиоаппаратуры будет заплачено 450 тыс.д.ед. и , таким образом, на мелкие покупки останется 30 тыс.д.ед. (480 – 450).

3) На оставшиеся 30 тыс.д.ед. должно быть сделано 5 (20-15) мелких покупок двух видов.

Если бы бытовая техника стоила 10 тыс.д.ед. за единицу, то 5 ее единиц обошлись бы в 50 тыс.д.ед., т.е. пришлось бы переплатить сверх задания 20 тыс.д.ед. (50-30) из-за переплаты по 5 тыс.д.ед. (10-5) на каждой единице. Поэтому приходится покупать менее 5 единиц бытовой техники, а 4 – всего на 20 тыс.д.ед. (4 * 5 тыс.д.ед.).

4) на оставшиеся 10 тыс.д.ед. (30-20) можно купить третий вид товара – одежду. Этого как раз хватит на 1 единицу одежды.

Итак, экспедитор покупает: 15 единиц радиоаппаратуры, 1 единицу одежды и 4 единицы бытовой техники.

 

 

 

 

 

 

 

 

 

 

 

 

 

ОТВЕТ:

Не только не переоценивает, но даже преуменьшает.

Возьмем в руки самый подробный каталог товаров. Вряд ли он будет иметь более 1000 страниц. Откроем его посередине, на 500-странице, и зададим 1-й вопрос: «задуманный товар находится на этой странице или после нее». Получив ответ, мы уменьшаем количество претендентов на задуманный товар ровно в 2 раза.

Продолжая таким же образом «половинить» каталог, на 10-м вопросе мы дойдем до одной его страницы, на которой и будет искомый товар.  Далее подобным же путем найдем один из двух столбцов, в которых располагаются товары (11-й вопрос).

В столбце вряд ли будет более 10 товаров. Чтобы «споловинить» и их, потребуется еще максимум 4 вопроса.

Итого 15 вопросов, и задача решена.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ОТВЕТ:

Действие чашечных весов основано на принципе рычага. Если правое плечо весов имеет длину П, левое - Л, и грузы, которые мы взвешиваем на правой и левой чашках, равны соответственно  и , то должно действовать известное из физики равенство:

П

Поскольку весы неисправны, при первом взвешивании вес гири Г соответствует Х кг товара, а при втором взвешивании — У кг товара.

Равновесие наступает при равенстве:

П  для первого взвешивания

Л   для второго взвешивания.

Из этих соотношений следует, что:

Х =

При этом общий вес товара равен:

Х + У =

Из алгебры известно, что (кроме случаев, когда

Доказательство: если П=Л и оба положительны, то (П-Л)²>0. Отсюда П²+2ПЛ+Л²>0, или П²+Л²>2ПЛ, или

Поэтому Х+У>2Г, т.е. Г <

Значит, фактический вес товара больше, чем полученный в результате предложенного способа взвешивания.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ОТВЕТ:

1) После первой замены бензина на колонке оставалось 36-12-24 т
высококачественного бензина. При этом в одном литре смеси высококачественный бензин составлял:

2) При второй замене в 9 т израсходованной смеси содержалось 9
высококачественного бензина. Следовательно, в оставшемся на колонке
бензине высококачественного было 24 – 6 = 18 т. А в одном литре смеси – соответственно

 

3) После третьей замены в 8 т израсходованной смеси содержалось 8 = 4 т высококачественного бензина. Следовательно, в оставшемся на колонке бензине высококачественного было 18 – 4 = 14 т.

14 т из 36 - это 39% высококачественного бензина и 61% (100-39) – низкосортного.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ОТВЕТ:

 

150 тонн

 

 

 

 

 

 

 

 

ОТВЕТ:

Пожалуй, дешевле всего будет перенести увеличенное изображение небольшого часового циферблата на экран, помещенный на башне, с помощью оптического проектора.

 

 

 

 

 

 

 

 

ОТВЕТ:

Отличаются: скорости оборота капитала, цены товара, расходы на
хранение (поддержание) товара.

Совпадать должна норма прибыли (прибыль за определенное время). Иначе необходимо менять товар.

 

 

 

 

 

 

 

 

 

 

 

 

 

ОТВЕТ:

 

Обозначая стоимость клипс через Кл, броши – Бр, кольца Кол и заколки - Зак, можно по условиям задачи составить следующие два уравнения:

Кл + Бр = 3  (Кол + Зак),

2(Кол + Бр) – Кл + Зак.

Совместное решение уравнений (1) и (2) даст искомый результат:

Кл = 735 д.ед.,

Кол = 260 д.ед.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ОТВЕТ:

Предположим, вторая крестьянка имела в К раз больше яиц, чем
первая. Так как они обе выручили одинаковые суммы, из сделанного предположения следует, что первая продавала яйца в К раз дороже, чем вторая.

Если бы перед торговлей они поменялись яйцами, то у первой было бы в К раз больше яиц, чем у второй, и она продавала бы их в К раз дешевле. При этом она выручила бы денег в К  К = К² раз больше второй.

Из этого следует отношение их выручек:

К² 1 = 15  6

К =  =

Деля 100 яиц в отношении 3:2, получим, что у первой крестьянки было 60 яиц, а у второй - 40.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ОТВЕТ:

Норма прибыли (рентабельность) рассчитывается по формуле:

НРПР =

Где НРПР – норма прибыли

ПР – прибыль

З – затраты.

ПР = 1000 – 750 = 250 рублей

НРПР =

 

 

 

 

 

 

 

 

ОТВЕТ:

 

Из формулы, приведенной в решении задачи 21, следует: НРПР =  или НРПР =

Где В - выручка

Откуда

З = = = 2000 рублей

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ОТВЕТ:

Норма накопления (НН) рассчитывается по формуле:

НН =

 

— масса прибыли, направленная на накопление,

 - масса прибыли, направленная на потребление.

НН =

 

 

 

 

 

 

 

 

ОТВЕТ:

 

По формулам, приведенным в решениях задач 21 и 22:

1) З = = = 20 млн. д.ед.

2)  В = З + ПР = 20 + 5 = 25 млн.д.ед.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ОТВЕТ:

По формулам, приведенным в решении задач 26 и 22:

Прибыль (ПР) рассчитывается п формуле:

ПР = В – (МЗ + НР + ЗЗП)

Где В –выручка

НР – накладные расходы

МЗ – материальные затраты

ЗЗП – затраты на зарплату

НРПР =  или НРПР =

Где НРПР – норма прибыли

ПР – прибыль

З – затраты.

1)  З=20+30+10=60 млн д.ед.;

ПР=100-60=40 млн д.ед.;

2) НРПР =

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ОТВЕТ:

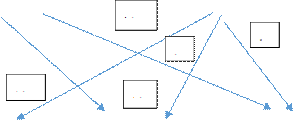
При горизонтальной организации каналов распределения товаров
(рис. Рис.а) каждый из производителей стремится направить свой товар по таким каналам, чтобы обеспечить себе наибольшую прибыль. При этом интересы производителей сталкиваются: одни и тот же канал может оказаться привлекательным для обоих производителей, а пропускная способность каждого канала ограничена. В итоге стихийно складывается распределение, один из возможных вариантов которого показан на рис.

При этом производитель товаров А получает прибыль, равную сумме произведений единиц товара, направляемых каждому из потребителей, на соответствующие эффективности.

ТАБЛИЦА эффективности

	№1	№2	№3
А	16	10	8
Б	12	18	6

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рис. а Горизонтальная организация каналов распределения

 

Прибыль производителя товара:

А=10x16+30x10+20x8=620.

Аналогично для производителя товара Б: Прибыль производителя товара

Б=40х12+0x18+0x6=480.

Производитель товара А оказался в явном выигрыше. Казалось бы, что может быть для него лучше? Не будем, однако, торопиться с выводами.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

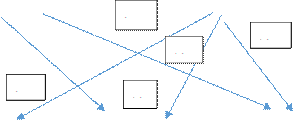
Рис. б Вертикальная организация каналов распределения

 

Рассмотрим возможную организацию распределения товаров (рис. б). В этом случае распределение товаров осуществляется в интересах не отдельного производителя товара, а системы в целом: принимается такое распределение, при котором суммарная прибыль обоих производителей будет максимальной. Для нахождения такого распределения (оно называется оптимальным) используются специальные методы. В простейших задачах данного типа решение может быть получено и глазомерно, путем подбора. На рис. б показано такое оптимальное распределение.

Величина суммарной прибыли обоих производителей товаров равна:

Общая прибыль производителей товаров А и Б равна:

50x16+0x10+10x8+0x12+30x18+10x6=1480.
Это существенно (на 35%) больше, чем суммарная прибыль при горизонтальном распределении (620+480=1100).

Разделив соответствующую вертикальному распределению общую прибыль пополам (1480:2), получим 740 единиц, что значительно больше, чем прибыль "победителя" при горизонтальном распределении товара (740-620=120).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ОТВЕТ:

Стоимость оптимальной партии товара (Попт) рассчитываются по формуле:

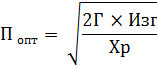где Г - годовая стоимость заказа,

Изг - стоимость издержек изготовления партии товара,

Хр - стоимость издержек хранения товара.

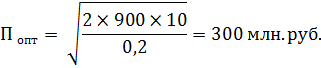Объем партии товара (Об) при этом равен:

Об =  = 30 тыс.штук.

Графическое решение данной задачи показано на рис.

 

 

 

 

 

 

 

 

 

 

 

 

 

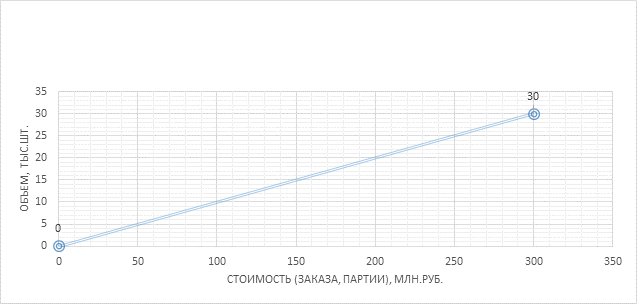
Рис. График определения стоимости партии оптимального размера

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ОТВЕТ:

 

1000 руб. стоит 1 кг орехов, или 400 г ядер. Следовательно, 1 кг ядер должен стоить в 2,5 раза (1000 г : 400 г) дороже, т.е. 2500 руб. Значит, выгоднее покупать неочищенные орехи.