Рабочий лист по теме "Текстовые задачи на смеси и сплавы""

Текстовые задачи на проценты, смеси и сплавы

1. При смешивании первого раствора кислоты, концентрация которого 20%, и второго раствора этой же кислоты, концентрация которого 50%, получили раствор, содержащий 30% кислоты. В каком отношении были взяты первый и второй растворы?

2. Имеется два сплава с разным содержанием меди: в первом содержится 60%, а во втором  — 45% меди. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 55% меди?

3. 21-процентного раствора некоторого вещества с таким же количеством 95-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

4. Первый сплав содержит 5% меди, второй  — 13% меди. Масса второго сплава больше массы первого на 4 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава.

5. Имеются два сосуда, содержащие 10 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 55% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 61% кислоты. Сколько килограммов кислоты содержится в первом растворе?

6. Свежие фрукты содержат 80% воды, а высушенные  — 28%. Сколько сухих фруктов получится из 288 кг свежих фруктов?

7.  Смешав 60%−ый и 30%−ый растворы кислоты и добавив 5 кг чистой воды, получили 20%−ый раствор кислоты. Если бы вместо 5 кг воды добавили 5 кг 90%−го раствора той же кислоты, то получили бы 70%−ый раствор кислоты. Сколько килограммов 60%−го раствора использовали для получения смеси?

Текстовые задачи на проценты, смеси и сплавы

1. При смешивании первого раствора кислоты, концентрация которого 20%, и второго раствора этой же кислоты, концентрация которого 50%, получили раствор, содержащий 30% кислоты. В каком отношении были взяты первый и второй растворы?

2. Имеется два сплава с разным содержанием меди: в первом содержится 60%, а во втором  — 45% меди. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 55% меди?

3. 21-процентного раствора некоторого вещества с таким же количеством 95-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

4. Первый сплав содержит 5% меди, второй  — 13% меди. Масса второго сплава больше массы первого на 4 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава.

5. Имеются два сосуда, содержащие 10 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 55% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 61% кислоты. Сколько килограммов кислоты содержится в первом растворе?

6. Свежие фрукты содержат 80% воды, а высушенные  — 28%. Сколько сухих фруктов получится из 288 кг свежих фруктов?

7.  Смешав 60%−ый и 30%−ый растворы кислоты и добавив 5 кг чистой воды, получили 20%−ый раствор кислоты. Если бы вместо 5 кг воды добавили 5 кг 90%−го раствора той же кислоты, то получили бы 70%−ый раствор кислоты. Сколько килограммов 60%−го раствора использовали для получения смеси?

Текстовые задачи на проценты, смеси и сплавы

1.  Тип 21 № 314508

На пост главы администрации города претендовало три кандидата: Журавлев, Зайцев, Иванов. Во время выборов за Иванова было отдано в 2 раза больше голосов, чем за Журавлева, а за Зайцева  — в 3 раза больше, чем за Журавлева и Иванова вместе. Сколько процентов голосов было отдано за победителя?

Решение. Заметим, что победителем на выборах окажется Зайцев. Пусть количество голосов, отданных за Зайцева равно x. Тогда за Журавлева и Иванова вместе отдали Процент голосов, отданных за Зайцева  

Ответ: 75%.

2.  Тип 21 № 314431

При смешивании первого раствора кислоты, концентрация которого 20%, и второго раствора этой же кислоты, концентрация которого 50%, получили раствор, содержащий 30% кислоты. В каком отношении были взяты первый и второй растворы?

Решение. Пусть первый раствор взят в количестве x грамм, тогда он содержит 0,2x грамм чистой кислоты, а второй раствор взят в количестве y грамм, тогда он содержит 0,5y грамм чистой кислоты. При смешивании двух этих растворов получится раствор массой x + y грамм, по условию задачи, он содержит 0,3(x + y) чистой кислоты. Следовательно, можно составить уравнение:

Выразим x через y: Следовательно, отношение, в котором были взяты растворы:

Ответ:

3.  Тип 21 № 314395

Имеется два сплава с разным содержанием меди: в первом содержится 60%, а во втором  — 45% меди. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 55% меди?

Решение. Пусть первый сплав взят в количестве x кг, тогда он будет содержать 0,6x кг меди, а второй сплав взят в количестве y кг, тогда он будет содержать 0,45y кг меди. Соединив два этих сплава, получим сплав меди массой x + y, по условию задачи он должен содержать 0,55(x + y) меди. Следовательно, можно составить уравнение:

Выразим x через y, получим, что Следовательно, отношение, в котором нужно взять сплавы,

Ответ: 2 : 1.

4.  Тип 21 № 353527

Смешали некоторое количество 21-процентного раствора некоторого вещества с таким же количеством 95-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

Решение. Пусть взяли x г 21-процентного раствора, тогда взяли и x г 95-процентного раствора. Концентрация раствора  — масса вещества, разделенная на массу всего раствора. В первом растворе содержится 0,21x г, а во втором  — 0,95x г Концентрация получившегося раствора равна или 58%.

Ответ: 58.

5.  Тип 21 № 316357

Первый сплав содержит 5% меди, второй  — 13% меди. Масса второго сплава больше массы первого на 4 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава.

Решение. Пусть масса первого сплава x кг. Тогда масса второго сплава (x + 4) кг, а третьего  — (2x + 4) кг. В первом сплаве содержится 0,05x кг меди, а во втором  — 0,13(x + 4) кг. Поскольку в третьем сплаве содержится 0,1(2x + 4) кг меди, составим и решим уравнение:

Значит, масса первого сплава равна 6 кг, тогда масса второго сплава равна 10 кг и масса третьего сплава равна 16 кг.

Ответ: 16 кг.

6.  Тип 21 № 348438

Имеются два сосуда, содержащие 10 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 55% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 61% кислоты. Сколько килограммов кислоты содержится в первом растворе?

Решение. Пусть концентрация первого раствора  — х, концентрация второго раствора  — y. Составим систему уравнений согласно условию задачи и решим ее:

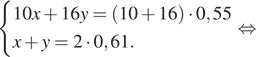
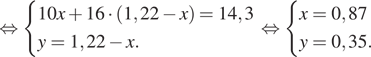
Таким образом, в первом растворе содержится килограмма кислоты.

Ответ: 8,7.

7.  Тип 21 № 338773

Свежие фрукты содержат 80% воды, а высушенные  — 28%. Сколько сухих фруктов получится из 288 кг свежих фруктов?

Решение. Заметим, что при сушке фруктов вода испаряется, поэтому необходимо рассматривать не количество воды, а количество питательного вещества, которое остается неизменным.

Свежие фрукты содержат 100% − 80%  =  20% питательного вещества, а высушенные  — 100% − 28%  =  72%. В 288 кг свежих фруктов содержится 0,2 · 288  =  57,6 кг питательного вещества. Такое количество питательного вещества будет содержаться в кг высушенных фруктов.

Ответ: 80 кг.

8.  Тип 21 № 311653

Смешав 60%−ый и 30%−ый растворы кислоты и добавив 5 кг чистой воды, получили 20%−ый раствор кислоты. Если бы вместо 5 кг воды добавили 5 кг 90%−го раствора той же кислоты, то получили бы 70%−ый раствор кислоты. Сколько килограммов 60%−го раствора использовали для получения смеси?

Решение. Пусть x кг и y кг  — массы первого и второго растворов, взятые при смешивании. Тогда кг  — масса полученного раствора, содержащего кг кислоты. Концентрация кислоты в полученном растворе 20%, откуда

Решим систему двух полученных уравнений:

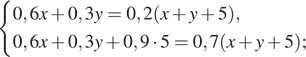
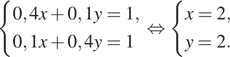
Замечание. Решение можно сделать несколько проще, если заметить, что из полученных уравнений следует: откуда Первое уравнение принимает вид откуда

Ответ: 2 кг.

Скачано с www.znanio.ru