Рациональные числа, иррациональные числа, конечные и бесконечные десятичные дроби

Класс__________Дата__________

Урок № ____

РАЦИОНАЛЬНЫЕ ЧИСЛА, ИРРАЦИОНАЛЬНЫЕ ЧИСЛА, КОНЕЧНЫЕ И БЕСКОНЕЧНЫЕ ДЕСЯТИЧНЫЕ ДРОБИ

Цели: повторить понятие рациональные, иррационального числа, действительного числа; закрепить навык преобразования обыкновенной дроби в десятичную и десятичной бесконечной периодической дроби в обыкновенную; развивать память, мышление.

Тип урока:  Урок  повторения учебного материала.

Ход урока:

1. Организационный момент

2. Актуализация знаний

Число  - основное понятие математики, используемое для количественной характеристики, сравнения, нумерации объектов и их частей.

Письменными знаками для обозначения служат цифры, а также символы математических операций.

3. Изучение нового материала

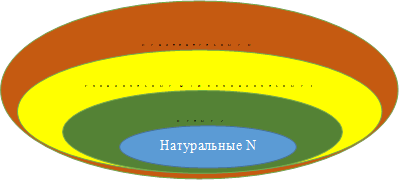Множество действительных чисел состоит из рациональных и иррациональных чисел. К рациональным числам относятся натуральные числа. Натуральные числа это те числа, с помощью которых мы ведем счет: 1, 2, 3, 4, 5 и т.к.

Если мы к натуральным числам добавляем противоположные им числа и число нуль, то мы получаем множество целых чисел.

Если мы к целым числам добавляем дробные числа, выраженные числителем и знаменателем, у которых числитель это целое число, а знаменатель натуральное число, то мы получаем множество рациональных чисел.

Всегда ли можно до конца поделить числитель на знаменатель? Не всегда. Например, 2:4 = 0,5, а 2:3=0,66666666….. Конечными называют дроби, которые содержат конечное число цифр после запятой. 0,5; 0,14; 0,063 и тд. Бесконечными называют дроби, которые содержат неопределенное количество цифр после запятой. 0,567452...; 54,7286462...; 3,376472973... и тд. Периодическая дробь – это бесконечная десятичная дробь, у которой, начиная с некоторого десятичного знака, повторяется одна и та же цифра или несколько цифр (период дроби). Какая дробь называется непериодической? (ответ учащихся)

Каждое рациональное число можно выразить в виде десятичной, бесконечной периодической дроби. Даже целые числа мы можем представить, как целое число и ноль в периоде.

- 1,666… 0,333… 1,5

-1,(6) -1,(0) 0,(3) 1,(0) 1,5(0) 2,(0)

Иррациональные числа. Приставка «ир» говорит нам, что это не рациональные числа. И в отличии от рациональных чисел иррациональные нельзя представить в виде дроби, у которой бы числитель был бы целым числом, а знаменатель – натуральным. Зато их можно представить в виде десятичной, бесконечной, непериодической дроби.

Мы видим, что периода здесь нет. И именно эти числа записываются с помощью корней. В данном случае это число можно записать как , а это  

Определение: Иррациональными называются числа, не являющимися рациональными, которые не могут быть представлены в виде дроби
, где а целое число, а б – натуральное. Иррационально число может быть представлено в виде бесконечной десятичной непериодической дроби

Задание: Вычислите:

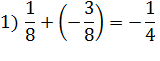
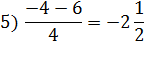
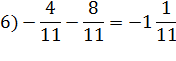
Дробные числа

Чтобы обратить чисто периодическую дробь в обыкновенную, нужно в числителе обыкновенной дроби поставить число, образованное из цифр, стоящих в периоде, а в знаменателе – написать цифру 9 столько раз, сколько цифр в периоде.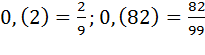

Для смешанной периодической дроби – в числителе записать всю дробную часть и вычесть из неё число, полученное из цифр до периода. В знаменателе записать столько девяток, сколько цифр в периоде и справа дописать столько нулей, сколько цифр в дробной части до периода..

4. Физкультминутка

5. Формирование умений и навыков

1. Найдите рациональные дроби, равные данным бесконечным периодическим десятичным дробям:

2. Решите задачу по краткому условию:

6. Итоги урока

Вопросы  учащимся:

- Какие числа называются рациональными, иррациональными?

- С какими видами десятичных дробей вы познакомились?

Домашнее задание: повт.конспект, выполнить задание в тетради.