Рациональные уравнения из материалов ЕГЭ базового уровня.

Рациональные уравнения из материалов ЕГЭ базового  уровня.

1.    Найдите корень уравнения:

Решение. Последовательно получаем:

 Ответ: −5.

Ответ: -5

26663

-5

Кодификатор ФИПИ/Решу ЕГЭ: 2.1.2 Рациональные уравнения

2. Найдите корень уравнения

Решение. Выполним преобразования, используя формулы и :

 Ответ: 3.

3. Решите уравнение

Решение. Используем формулы квадрата суммы и разности:

 Ответ: −6.

Ответ: -6

77369

-6

Кодификатор ФИПИ/Решу ЕГЭ: 1.4.2 Преобразования выражений, включающих операцию возведения в степень, 2.1.2 Рациональные уравнения

4.Найдите корень уравнения Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Решение. Переведем число в правой части уравнения в неправильную дробь и умножим обе части уравнения на 3, получаем:

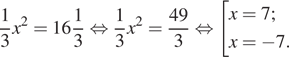
Ответ: −7.

5. Найдите корень уравнения: Если уравнение имеет более одного корня, укажите меньший из них.

Решение. Решим квадратное уравнение:

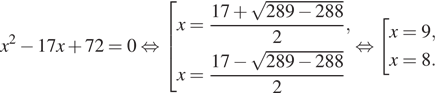
 Ответ: 8.

6. Найдите корень уравнения

Решение. Извлекая кубический корень из обеих частей уравнения, получаем откуда

Ответ: −1.

7. Решите уравнение Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Решение. Область определения уравнения задается соотношением На области определения имеем:

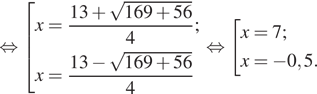
 Оба найденных решения удовлетворяют условию меньший из них равен −0,5.

 Ответ: −0,5.

8. Найдите корень уравнения:

Решение. Последовательно получаем:

 Ответ: 1.

9. Решите уравнение Если уравнение имеет более одного корня, в ответе запишите больший из корней.

Решение. Дроби с одинаковыми числителями равны в двух случаях: а) знаменатели этих дробей равны и при этом отличны от нуля; б) числители дробей равны нулю, при этом все знаменатели отличны от нуля. Получаем:

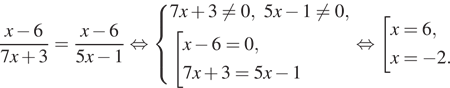
Больший из найденных корней равен 6.

 Ответ: 6.

                                                            Решить самостоятельно.

1.    Найдите корень уравнения Если уравнение имеет более одного корня, в ответе запишите больший из корней.

2.    Найдите корень уравнения:

3.    Найдите корень уравнения

4.    Найдите корень уравнения

Ответы.

1.       5

2.      0,3

3.       7

4.       -94

Скачано с www.znanio.ru