
Рациональные уравнения из материалов ЕГЭ профильного уровня.
1. а) Решите уравнение ![]()
б) Найдите его корни, принадлежащие отрезку ![]()
Решение. а) Сделаем
замену ![]() возведём
обе части в квадрат
возведём
обе части в квадрат
![]()
![]()
тогда ![]() Имеем:
Имеем:
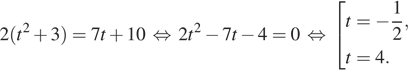
Вернемся к исходной переменной. Если ![]() то
то

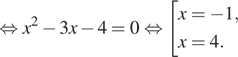
Если ![]() то
то
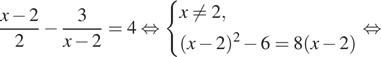
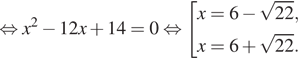
б) Выясним, какие из найденных корней принадлежат
отрезку ![]() В силу
неравенств
В силу
неравенств
![]() и
и ![]()
из найденных корней уравнения заданному отрезку принадлежат только
числа ![]() и
и ![]()
Ответ: а) ![]() б)
б)
![]()
2.
а) Решите уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. а) При
условии ![]() отбросим
знаменатели, затем применим формулу разности квадратов:
отбросим
знаменатели, затем применим формулу разности квадратов:
![]()
![]()
![]()
![]()
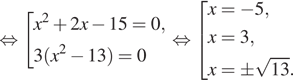
По условию подходят только x = −5, x = 3,
![]()
б) Заметим, что ![]() Кроме
того,
Кроме
того,
![]()
![]()
Последнее неравенство верно, т. к. ![]() следовательно, подходит только x = 3.
следовательно, подходит только x = 3.
Ответ: а) ![]() б)
x = 3.
б)
x = 3.
3.
а) Решите уравнение ![]()
б) Найдите его корни, принадлежащие отрезку ![]()
Решение. а) Сделаем
замену ![]() тогда
тогда
![]() Имеем:
Имеем:
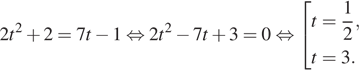
Вернемся к исходной переменной. Если ![]() то
то
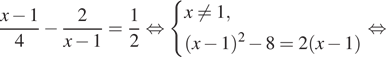
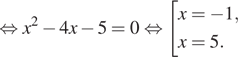
Если ![]() то
то
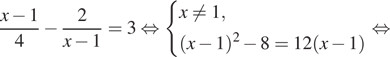
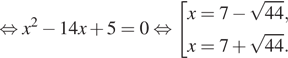
б) Выясним, какие из найденных корней принадлежат
отрезку ![]() В
силу неравенств
В
силу неравенств
![]()
из найденных корней уравнения заданному отрезку принадлежат только
числа ![]() и
и ![]()
Ответ: а) ![]() б)
б)
![]()
4.
а) Решите уравнение ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. а) Внесем
число 2 в скобки и обозначим ![]() Заметим,
что
Заметим,
что ![]() а
значит, уравнение записывается в виде
а
значит, уравнение записывается в виде ![]() откуда
откуда ![]() или
или ![]() Далее при условии
Далее при условии ![]() имеем:
имеем:
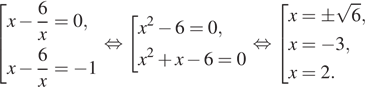
б) Заметим, что ![]() Подходят
Подходят
![]() и 2.
и 2.
Ответ: а) ![]() б)
б)
![]() 2.
2.
5.
а) Решите уравнение ![]()
б) Найдите его корни, принадлежащие отрезку ![]()
Решение. а) Пусть ![]() тогда
тогда
![]() Имеем:
Имеем:
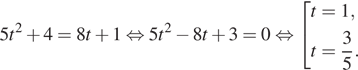
Вернемся к исходной переменной. Если ![]() то
то
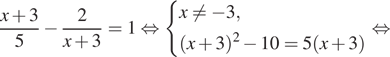
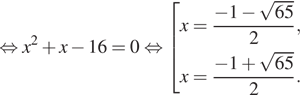
Если ![]() то
то
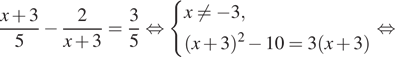
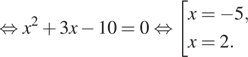
б) Выясним, какие из найденных корней принадлежат
отрезку ![]() Положительные
корни не могут лежать в этом отрезке. Число –5 лежит в нем. Корень
Положительные
корни не могут лежать в этом отрезке. Число –5 лежит в нем. Корень ![]() тоже
лежит в этом отрезке в силу цепочки соотношений:
тоже
лежит в этом отрезке в силу цепочки соотношений:

![]()
Ответ: а) 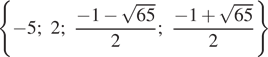 б)
б)
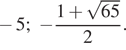
6. Постройте график функции ![]() и
определите, при каких значениях
и
определите, при каких значениях ![]() прямая
прямая
![]() имеет
с графиком ровно одну общую точкуРешение.
имеет
с графиком ровно одну общую точкуРешение.
Упростим выражение для функции:
![]() (при
(при![]() ).
).
Таким образом, получили, что график нашей функции сводится
к графику функции ![]() с
выколотой точкой
с
выколотой точкой ![]()
Построим график функции (см. рисунок).
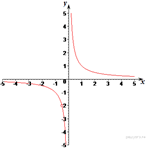
Заметим, что прямая ![]() проходит
через начало координат и будет иметь с графиком функции ровно одну
общую точку только тогда, когда будет проходить через выколотую точку
проходит
через начало координат и будет иметь с графиком функции ровно одну
общую точку только тогда, когда будет проходить через выколотую точку ![]() Подставим
координаты этой точки в уравнение прямой и найдём коэффициент
Подставим
координаты этой точки в уравнение прямой и найдём коэффициент ![]()
![]()
Ответ: 4.
7. Сократите дробь
![]()
Решение.
Последовательно разделим многочлен на одночлены в столбик:
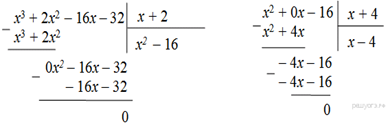
Ответ: ![]()
Приведём другое решение.
Разложим числитель на множители, используя метод группировки:
![]()
8.
Постройте
график функции ![]() и
найдите все значения k, при которых прямая
и
найдите все значения k, при которых прямая ![]() имеет
с графиком данной функции ровно одну общую точку.
имеет
с графиком данной функции ровно одну общую точку.
Задание 23 № 311827
Решение.
Раскрывая модули, получаем, что при ![]() функция
принимает вид
функция
принимает вид ![]() при
при
![]() функция
принимает вид
функция
принимает вид ![]() а
при
а
при ![]() функция
принимает вид
функция
принимает вид ![]()
График функции изображён на рисунке.
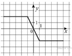
Прямая ![]() имеет
с графиком данной функции ровно одну общую точку при
имеет
с графиком данной функции ровно одну общую точку при ![]() принадлежащем
множеству
принадлежащем
множеству ![]()
Ответ: ![]()
Решить самостоятельно.
1. Постройте
график функции ![]() И определите,
при каких значениях
И определите,
при каких значениях ![]() прямая
прямая
![]() имеет
с графиком ровно одну общую точку.
имеет
с графиком ровно одну общую точку.
2. При
каких положительных значениях ![]() прямая
прямая
![]() имеет
с параболой
имеет
с параболой ![]() ровно
одну общую точку? Найдите координаты этой точки и постройте данные графики
в одной системе координат.
ровно
одну общую точку? Найдите координаты этой точки и постройте данные графики
в одной системе координат.
Ответы и решения.
1. Решение.
Упростим выражение:
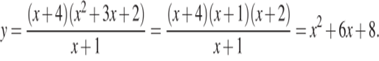
График функции сводится к графику параболы ![]() с
выколотой точкой
с
выколотой точкой ![]()
Этот график изображён на рисунке:
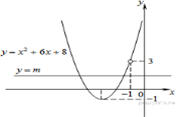
Из графика видно, что прямая ![]() имеет
с графиком функции ровно одну общую точку при
имеет
с графиком функции ровно одну общую точку при ![]() и
и
![]()
Ответ: −1; 3.
2. Решение.
Найдём абсциссы точек пересечения:
![]()
Графики функций, будут иметь ровно одну точку пересечения, если это уравнение имеет ровно одно решение. То есть, если дискриминант этого квадратного уравнения будет равен нулю.
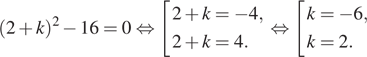
По условию ![]() поэтому
нам подходит значение
поэтому
нам подходит значение ![]()
Подставив параметр ![]() в
уравнение, найдём
в
уравнение, найдём ![]() координату
точки пересечения этих функций:
координату
точки пересечения этих функций:
![]()
Координата ![]() находится
путём подстановки координаты
находится
путём подстановки координаты ![]() в
любое из уравнений, например, в первое:
в
любое из уравнений, например, в первое:
![]()
Теперь, зная ![]() можем
построить графики обеих функций (см. рисунок).
можем
построить графики обеих функций (см. рисунок).
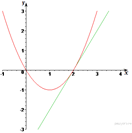
Ответ: (2; 0).
Скачано с www.znanio.ru
а) ![]() б)
б)
![]() 2.
2.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.