Разработка

План урока

1.Класс: 8                 

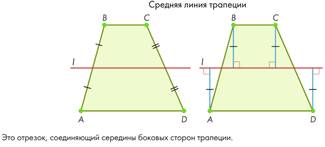
2.Тема: Трапеция, ее средняя линия                   

3.Тип урока: Урок освоения новых знаний и умений

4.Цель урока: выяснить уровень знаний учащихся по теме «Квадратный трехчлен».

5.Планируемые результаты:

Личностные: овладение основными навыками исследовательской деятельности, установка на осмысление опыта, наблюдений, поступков и стремление совершенствовать пути достижения индивидуального и коллективного благополучия.

Предметные: распознавать геометрические фигуры на плоскости, определять их взаимное расположение, изображать геометрические фигуры.

6.Ключевые слова: трапеция, прямоугольная трапеция, средняя линия трапеции, равнобедренная трапеция.

7.На уроке предусмотрено использование следующих видов деятельности:«Галерея изображений (группа изображений по одной тематике)», «Самостоятельная работа».

Блочно-модульное описание урока

Этап 1/БЛОК 1. Освоение нового материала

1. Осуществление учебных действий по освоению нового материала.

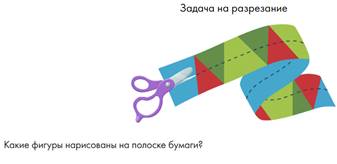
Первые две задачи обязательно разобрать в классе - это признаки средней линии трапеции, которые будут использоваться в будущем.

Третью задачу можно пропустить

В четвёртой можно рассказать решение, по которому точка R равноудалена от трёх сторон трапеции, так как лежит на биссектрисах, и из этого вывести требуемое.

(Библиотека ЦОК https://m.edsoo.ru/88673064 )

Этап 2 /БЛОК 2. Применение изученного материала

1. Применение знаний, в том числе в новых ситуациях.

Задачи на применение свойств средней линии трапеции. Обратите внимание на 4ю задачу - она довольно изящно решается именно через трапеции, несмотря на то, что изначальная задача про квадрат. Разберите её в классе.(Библиотека ЦОК https://m.edsoo.ru/88673064 )

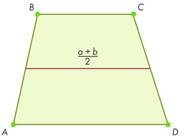Задача 1.Известно, что отрезок с концами на боковых сторонах трапеции параллелен её основаниям и равен половине их суммы. Докажите, что данный отрезок — средняя линия трапеции.

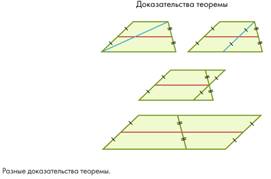
Решение

Проведя среднюю линию, получим, что она образует с нашим отрезком параллелограмм, что невозможно при их несовпадении.

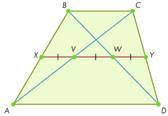
Задача 2. Диагонали трапеции делят её среднюю линию на три равные части. Найдите отношение оснований трапеции, большей к меньшей.

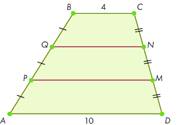
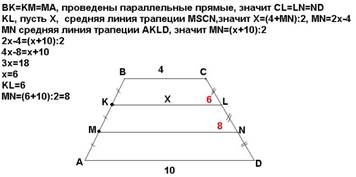
Задача 3. Основания трапеции равны 4 и 10. Каждая из боковых сторон AB и CD разделена двумя точками P, Q и M, N соответственно на 3 равные части (см. рисунок). Найдите QN, если BC || QN.

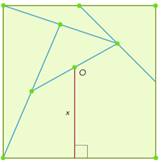
Задача 4.Сторона квадрата равна 1. Каждая из отмеченных на рисунке точек является серединой своего отрезка. Найдите показанное на этом рисунке расстояние от точки O до стороны квадрата.

2.Выполнение заданий в формате ГИА (ОГЭ, ЕГЭ).

Скажите школьникам, что эта задача является примером задачи из ОГЭ на данную тему. Предложить её решить школьникам и желательно с ними разобрать.(Библиотека ЦОК https://m.edsoo.ru/88673064 )

Задача 1.Основания трапеции равны 8 и 18, а высота равна 5. Найдите среднюю линию этой трапеции.

Решение

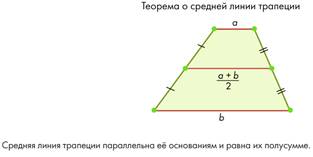
Средняя линия трапеции равно полусумме её оснований. Значит, она равна 

8+18:2=13.

Ответ: 13.

Этап 3 /БЛОК 3. Подведение итогов, домашнее задание

1. Рефлексия.

Обсуждаем итоги урока, выставляем оценки в журнал.

1.Что на уроке больше всего понравилось (запомнилось)?

2.Что было трудным?

3.Что так и осталось непонятным?

2. Домашнее задание.

Первые три задачи на повторение материала. Последние две заставят учащихся поиграть с картинкой. Подскажите им найти в этих задачах всё, что они смогут.

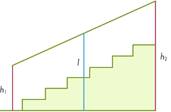
Задача 1.Перила лестницы дачного дома для надёжности укреплены посередине вертикальным столбом. Найдите высоту l этого столба, если наименьшая высота h1 перил равна 0,7 м, а наибольшая — h2 равна 1,5 м. Ответ дайте в метрах.

Задача 2.На сторонах AB и BC треугольника ABC отметили точки X и Y так, что BX = 3AX и BY = 3CY. Найдите XY, если AC = 12.

Задача 3.Дана равнобедренная трапеция ABCD. Перпендикуляр, проведённый из вершины B к большему основанию AD, делит это основание на два отрезка, больший из которых равен 7 см. Найдите среднюю линию трапеции, ответ выразите в см.

Задача 4.Диагональ прямоугольной трапеции с углом 60° и её боковая сторона равны. Найдите среднюю линию трапеции, если боковая сторона равна 14.

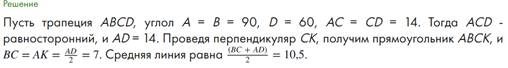
№793, стр. 208, п.88.

Скачано с www.znanio.ru