Разработка 7

“Бесконечно убывающая геометрическая прогрессия”

Цель урока: ознакомление учащихся с новым видом последовательности – бесконечно убывающей геометрической прогрессией.

Задачи:

формулирование начального представления о пределе числовой последовательности; знакомство с ещё одним способом обращения бесконечных периодических дробей в обыкновенные с помощью формулы суммы бесконечно убывающей геометрической прогрессии;

развитие интеллектуальных качеств личности школьников такие, как логическое мышление, способность к оценочным действиям, обобщению;

воспитание активности, взаимопомощи, коллективизма, интереса к предмету.

Оборудование: компьютерный класс, проектор, экран.

Тип урока: урок – усвоение новой темы.

Ход урока

I. Орг. момент. Сообщение темы и цели урока.

II. Актуализация знаний учащихся.

В 9 классе вы изучали арифметическую и геометрическую прогрессии.

Вопросы

1. Определение арифметической прогрессии.

    (Арифметической прогрессией называется последовательность, каждый член которой,

    начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом).

2. Формула n-го члена арифметической прогрессии

    (   )

3. Формула суммы первых n членов арифметической прогрессии.

    (   или   )

4. Определение геометрической прогрессии.

    (Геометрической прогрессией называется последовательность отличных от нуля чисел,

    каждый член которой, начиная со второго, равен предыдущему члену, умноженному на

    одно и то же число).

5. Формула n-го члена геометрической прогрессии

    (   )

6. Формула суммы первых n членов геометрической прогрессии.

    ()

7. Какие формулы вы еще знаете?

    (, где ;   ;

    ;   , )

Задания

1. Арифметическая прогрессия задана формулой           a_n = 7 – 4n. Найдите a₁₀.   (-33)

2. В арифметической прогрессии a₃ = 7 и a₅ = 1. Найдите a₄.   (4)

3. В арифметической прогрессии a₃ = 7 и a₅ = 1. Найдите a₁₇.   (-35)

4. В арифметической прогрессии a₃ = 7 и a₅ = 1. Найдите S₁₇.   (-187)

5. Для геометрической прогрессии    найдите пятый член.   

6. Для геометрической прогрессии    найдите n-й член.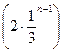   

7. В геометрической прогрессии   b₃ = 8 и b₅ = 2. Найдите b₄.   (4)

8. В геометрической прогрессии   b₃ = 8 и b₅ = 2. Найдите b₁ и q.  

9. В геометрической прогрессии   b₃ = 8 и b₅ = 2. Найдите S₅.   (62)

III. Изучение новой темы (демонстрация презентации).

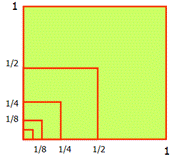
Рассмотрим квадрат со стороной, равной 1. Нарисуем ещё один квадрат, сторона которого равна половине первого квадрата, затем ещё один, сторона которого – половина второго, потом следующий и т.д. Каждый раз сторона нового квадрата равна половине предыдущего.

В результате, мы получили последовательность сторон квадратов образующих геометрическую прогрессию со знаменателем .

И, что очень важно, чем больше мы будем строить таких квадратов, тем меньше будет сторона квадрата. Например,

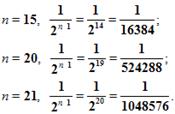
Т.е. с возрастанием номера n члены прогрессии приближаются к нулю.

С помощью этого рисунка можно рассмотреть и ещё одну последовательность.

Например, последовательность площадей квадратов:

.   И, опять, если n неограниченно возрастает, то площадь, как угодно близко приближается к нулю.

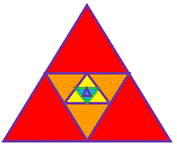
Рассмотрим ещё один пример. Равносторонний треугольник со стороной равной 1см. Построим следующий треугольник с вершинами в серединах сторон 1-го треугольника, по теореме о средней линии треугольника – сторона 2-го равна половине стороны первого, сторона 3-го – половине стороны 2-го и т.д. Опять получаем последовательность длин сторон треугольников.

 при .

Если рассмотреть геометрическую прогрессию с отрицательным знаменателем.

То, опять, с возрастанием номера n члены прогрессии приближаются к нулю.

Обратим внимание на знаменатели этих последовательностей. Везде знаменатели были меньше 1 по модулю.

Можно сделать вывод: геометрическая прогрессия будет бесконечно убывающей, если модуль её знаменателя меньше 1.

Фронтальная работа.

Определение:

Геометрическая прогрессия называется бесконечно убывающей, если модуль её знаменателя меньше единицы.                   .

С помощью определения можно решить вопрос о том, является ли геометрическая прогрессия бесконечно убывающей или нет.

Задача

Является ли последовательность бесконечно убывающей геометрической прогрессией, если она заданна формулой:

;      .

Решение:

. Найдем q.

;   ;   ;   .

данная геометрическая прогрессия является бесконечно убывающей.

б)  данная последовательность не является бесконечно убывающей геометрической прогрессией.

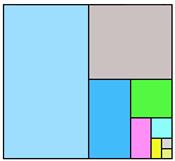
Рассмотрим квадрат со стороной, равной 1. Разделим его пополам, одну из половинок ещё пополам и т.д. площади всех полученных прямоугольников при этом образуют бесконечно убывающую геометрическую прогрессию:       

Сумма площадей всех полученных таким образом прямоугольников будет равна площади 1-го квадрата и равна 1.    

Но в левой части этого равенства – сумма бесконечного числа слагаемых.

Рассмотрим сумму n первых слагаемых.

По формуле суммы n первых членов геометрической прогрессии, она равна .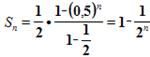

Если n неограниченно возрастает, то

или . Поэтому , т.е. .

Сумма бесконечно убывающей геометрической прогрессии есть предел последовательности S₁, S₂, S₃, …, S_n, … .

Например, для прогрессии  ,

имеем  

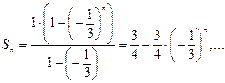   Так как  

Сумму бесконечно убывающей геометрической прогрессии можно находить по формуле .

III. Осмысление и закрепление (выполнение заданий).

№13;   №14;   №15(1,3);       №16(1,3);       №18(1,3);        №19;   №20.

IV. Подведение итогов.

С какой последовательностью сегодня познакомились?

Дайте определение бесконечно убывающей геометрической прогрессии.

Как доказать, что геометрическая прогрессия является бесконечно убывающей?

Назовите формулу суммы бесконечно убывающей геометрической прогрессии.

V. Домашнее задание.

1. Читать § 2 (с. 133-137)

2. № 15(2,4); №16(2,4); 18(2,4).