Разработка 8

Тема: Понятие функции.

Цели:

• формирование и первичная отработка понятий “функция”, “аргумент функции”, “значение функции”, “независимая переменная”, “зависимая переменная”;
• формирование представлений о способах задания функций;
• начать выработку умений строить и читать графики функций;
• отработка умений решения простейших задач, опираясь на графики и таблицы;

·         формировать у учащихся познавательный интерес к алгебре.

Оборудование:

• мультимидийный проектор;

Ход урока

I.Организационный момент.

Тема урока. Цели урока. (повторение решение уравнений)

II. Актуализация темы.

Краткая беседа о том, что в окружающем мире абсолютно всё находится в какой-либо зависимости от чего-либо. Примеры. (С опорой на учащихся, дать волю их фантазии, причём возможны самые нелепые примеры с точки зрения математики: например, настроение зависит от погоды). Математика нашла способы описания зависимостей.

III. Изучение нового материала.

1) Составьте выражения для решения данных задач.

1. Автомобиль  движется из Бузулука в Оренбург со скоростью 80 км/ч. Какой путь пройдет поезд за t часов?          S = 60t

2.      Чему равна площадь квадрата со стороной “а” см?       S_кв.= а²     

2)Зависимость  одной величины от другой .

Мы указали формулу, позволяющую для каждого значения одной переменной однозначно вычислить значение другой переменной.

1. Значения пути зависят от выбора значений времени.

     2.  Площадь квадрата зависит от длины его стороны. Если изменить длину стороны квадрата, то изменится и значение площади.

                    S = aa

                                Если а=3, то S=3•3=9(кв.ед.)      

                                Если а=0,4, то S=0,4•0,4 = 0,16(кв.ед.)

    3. Значения веса зависят от выбора значений цены.

3) Другие примеры зависимостей .

n   Периметр квадрата зависит от длины его стороны.

n  Длина окружности зависит от длины его радиуса.

n  Пройденный путь зависит от его скорости.

4) Описание зависимостей с помощью формул.

n  Р = 4а ( р зависит от а)

n  С=2пR (с зависит от R)

n  S = t v (  s зависит от v )

Если переменные а, R , v  обозначить буквой  х, а переменные   P, C, S обозначить буквой у, то получатся формулы звисимостей  у от х .

n  У = 4х

n  У = 2пх

n  У = tх

5)Зависимость  одной величины от другой (с помощью таблицы)

В таблице показана зависимость количества выпущенных заводом машин от порядкового номера месяца, в котором были выпущены машины.

6) Зависимость одной величины от другой (графически)

7) В результате этой работы дается понятие

n  независимой переменной

n  аргумента функции

n  области определения функции

n  зависимой переменной

n  значения функции

n  области значений функции

8) Что же такое функция? (определение функции).

Функцией называют  такую зависимость переменной у от переменной х, при которой  каждому      значению х  (независимой переменной) соответствует  единственное   значение у (зависимой переменной).

9) Способы задания функции.

1. Словесный.

Вспомним  пословицы. Ведь пословицы – это тоже отражение устойчивых закономерностей, выверенное многовековым опытом народа. Учитель называет пословицу, учащиеся определяют зависимые и независимые величины:

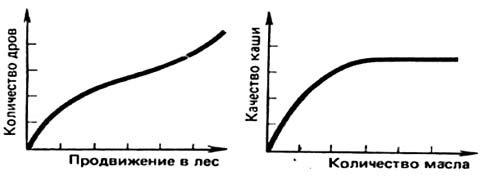
 “Чем дальше в лес, тем больше дров”. Количество дров нарастает по мере продвижения вглубь леса – от опушек, где все давным-давно собрано, до чащоб, куда еще не ступала нога заготовителя.

“Каши маслом не испортишь”.

2. Таблицей.

Составьте зависимость между “х” и “у”, анализируя таблицу и запишите эту зависимость в виде формулы (у = х²).

3. Функция может быть задана формулой:

 у = х²; у = 2х; S = 50t.

4) Графиком.

IV. Закрепление.

 Задания №55, № 54

V. Факты из истории.

n  Термин «функция» - от латинского  function -  совершение, выполнение

n  Первоначально  понятие функции как выражения сложилось в 17 веке

n  В 18 веке основным объектом изучения математики стали зависимости между  переменными величинами

n  Впервые термин функция ввёл И.Бернулли в 1718 году

n  В общем виде определение функции было дано Н.И. Лобачевским в 1934 г.

VI.Домашнее задание

n  Читать П 1.5, стр. 22 – 25, выучить определение функции и значения  новых терминов

n  № 53, № 56,№ 58

n  Найти дополнительный материал по теме «История появления понятия «функция» (для желающих)

VII. Итоги урока.

 Что должны были усвоить и как усвоили. Что нового открыли для себя на уроке.          

 Дайте ответы на вопросы.

n  Как вы поняли, что такое функция?

n  Приведите два  примера зависимости одной величины от другой

n  Какими способами может быть задана функция?

n  Как иначе можно назвать  независимую переменную ?

n  Как иначе можно назвать  зависимую переменную?