Разработка 8

тема урока. Понятие рационального уравнения

Цели: ввести понятие рационального уравнения, формировать умение применять алгоритм решения рационального уравнения. Развивать математическую речь, логическое мышление, интерес к предмету. Воспитывать прилежание, трудолюбие, аккуратность, точность.

Планируемые результаты:

Личностные: умение контролировать, оценивать и анализировать процесс и результат учебной и математической деятельности; критичность мышления, инициатива, находчивость, активность при решении математических задач.

Предметные :знать:формулу нахождения корней квадратного уравнения; уметь вычислять квадратные корни, применять понятие и свойства квадратного корня при решении различных задач, решать квадратные уравнения с помощью формулы нахождения корней квадратного уравнения

Тип урока: формирование умений и навыков

Формы работы: фронтальная, индивидуальная

Методы и приёмы: самостоятельная, устный счёт, сравнение

Оборудование:  учебник, таблица

Ход урока

I. Организационный момент.

II. Проверка домашнего задания.

III. Устная работа.

1. Какие из выражений являются целыми, какие – дробными?

а) ;                  б) (а – b)² – 3ab;             в) ;

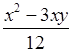г) ;               д) ;                  е) .

2. Решить уравнение: 3х²-4х-4=0

IV. Объяснение нового материала.

Объяснение следует проводить в  н е с к о л ь к о   э т а п о в.

1. В в е д е н и е   п о н я т и я рационального уравнения.

Во время проведения устной работы были актуализированы следующие знания учащихся: целые выражения, дробные выражения, рациональные выражения, допустимые значения переменных. Предлагаем учащимся самим сформулировать понятие дробного рационального уравнения. Следует акцентировать их внимание на то, что наличие дроби в выражении не свидетельствует о том, что это дробное выражение (уравнение), необходимо присутствие переменной в знаменателе дроби.

2. Р а с с м о т р е н и е   а л г о р и т м а  решения рационального уравнения.

Рассматривая способ решения дробного рационального уравнения, учащиеся используют приём аналогии: решая целое уравнение с числом в знаменателе, они умножают обе части уравнения на общий знаменатель, что позволяет избавиться от дробей. Возникает идея применить этот приём для нового вида уравнений. После домножения обеих частей уравнения на общий знаменатель, обращаем внимание учащихся, что произошло с областью допустимых значений уравнения. Она «расширилась» и теперь допустимыми стали любые значения переменных, то есть полученное уравнение не равносильно исходному.

Вопрос: как же следует поступить в этом случае? Затем формулируется алгоритм решения дробного рационального уравнения:

V. Формирование умений и навыков.

Устно №290

№291 а)да;  б) да;  в) да;  г) да;  д) да;  е) да;  ж) нет;  з) нет;  и)нет;  к)нет.

№ 292(а,б,в,г)

а)если х=2, то  3*2 -  = 2+5, 6 +  = 7, 6+1=7, 7=7. Ответ: является.

б) если х = -0,1, то 3*(-0,1-8)=4-2*(-0,1-1), 3*(-8,1)=4-2*(-1,1), -24,3=4+2,2, -24,3=6,2. Ответ: не является.

в)если х = 3, то 3²+4*3-28=0, 9+12-28=0,  -7=0. Ответ: не является.

г) если х = , то  – 1 = ,- : () -1=,   * -1=,   -  =, -  = 1,35. Ответ: не является.

№ 293(а.д,е,з)

VI. Итоги урока.

В о п р о с ы   у ч а щ и м с я:

– Какое уравнение называетсярациональным?

– Приведите примеры целого и рационального уравнения.

– Сформулируйте алгоритм решениярационального уравнения.

– Какими способами можно исключить «посторонние» корни рационального уравнения?

Домашнее задание: №292(д,е,ж,з),  № 293(б,в,г,ж)