Разработка 8

«Построение графиков функций, содержащих модули»

Тема урока:

Построение графиков функций, содержащих модули

Педагогические цели и задачи:

1.     Развитие личности

·         формирование информационной культуры;

·         общая информационная подготовка ученика как пользователя.

2.     Интенсификация учебно-воспитательного процесса

·         активизация познавательной активности учащихся;

·         повышение эффективности и качества обучения.

3.     Методические задачи, решаемые средствами ИКТ

·         визуализация знаний;

·         доступ к большому объему информации, представленному в занимательной форме, благодаря использованию средств мультимедиа;

·         формирование умений обрабатывать информацию;

·         усиление мотивации обучения (средства мультимедиа);

·         развитие наглядно-образного мышления;

·         формирование культуры учебной деятельности.

Цели урока:

Образовательные

• Продолжить формирование навыков построения графиков функций, содержащих модуль; обратить внимание на геометрический смысл модуля.
• Научить применять полученные знания при построении графиков квадратичной функции.

Развивающие

• Развивать навыки построения графиков функций.
• Формировать навыки логического мышления (сравнение, анализ, обобщение, выделение главного).
• Развивать познавательную активность.

Воспитывающие

• Продолжить воспитание интереса к предмету математики, воспитание любознательности, чувства ответственности, самоконтроля и самоанализа.

Тип урока: Урок открытия новых знаний, обретения новых умений и навыков.

Вид урока:  Мультимедиа - урок.

Оборудование:  Индивидуальные карточки  для контроля и самоконтроля учащихся, презентация по теме, мультимедиа-проектор.

Методы обучения:

• Словесные: рассказ, беседа.
• Наглядные: метод демонстрации.
• Практический метод: работа по построению графиков функций.
• Частично-поисковый метод.

Способы контроля:

• Текущий контроль: во время письменных ответов на вопросы и заполнения таблиц.
• Итоговый контроль: в форме устного опроса  по теме урока.

Ожидаемые результаты: В результате данного урока учащиеся должны научиться строить графики функций, которые содержат знак абсолютной величины, знать основные приемы построения, обращать внимание на особые точки функций, уметь анализировать и оценивать свои действия и результаты.

Структура урока

Организационный момент

1.     Мотивационный этап (ребус, устный опрос - основные понятия и формулировки, математический диктант)

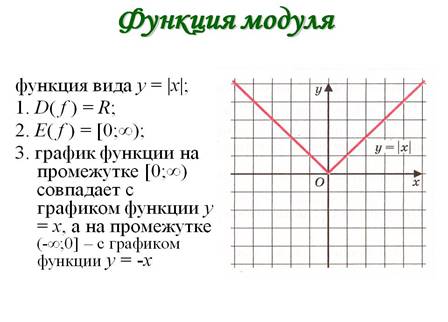
2.     Актуализация опорных знаний и осуществление первого пробного действия  (понятие модуля числа,  геометрический смысл модуля, график модуля)

3.     Выявление затруднений (устная работа с таблицей)

4.     Разработка проекта, плана по выходу из создавшегося затруднения, поиск оптимального решения

5.     Реализация выбранного плана. «Открытие новых знаний»

6.     Первичное закрепление новых знаний (разбор графиков на примерах).

7.     Включение в систему знаний и умений (построение графиков на примерах, задание - установить соответствие)

8.     Рефлексия, самоанализ, выставление оценок, рефлексия чувств и эмоций.

Ход урока

Организационный момент

1.     Мотивационный этап

(Модуль)

Вопросы:

1.     А что означает этот термин?

2.     Дайте определение модуля.

3.     Кто ввел понятие модуля?

4.     А кто ввел в обращение знак модуля?

5.     А когда?

6.     В чем заключается геометрический смысл модуля?

7.     Что собой представляет график функции модуля?

8.     ООФ, ОЗФ?

Математический диктант

1.     Может ли быть отрицательным значение суммы 2+|x|?

2.     Может ли равняться нулю значение разности 2|x| - |x|?

3.     При каких значениях y верно равенство – y = |-y|?

4.     Решите уравнение |x- 2| = 5

5.     В каких четвертях расположен график функции y = |x|

6.     Верно ли утверждение

7.      

Ответы:

2.     Актуализация опорных знаний и осуществление первого пробного действия

Термин (module) в буквальном переводе с латинского означает «мера». Это понятие было введено в математику в  19 веке английским учёным Р. Котесом учеником Ньютона. А немецкий математик К. Вейерштрасс ввёл в обращение знак модуля — символ, которым это понятие обозначается при написании.

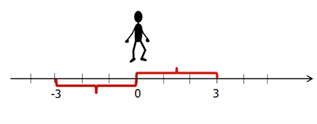
Геометрический смысл модуля заключается в том, что это расстояние от нуля до данного числа.

3.     Выявление затруднений  (Устная работа с таблицей)

Необходимо указать номера примеров, где есть ошибка.

Ответы:

Постройте схематично график функции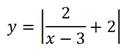

4.     Разработка проекта, плана выхода из создавшегося затруднения, поиск оптимального решения

Основные виды:    

y = x² – 8|x| + 12.

y = |x² – 8x + 12|.

y = |x² – 8|x| + 12|.

Изучение новой темы по плану:

1) Построение графика функции 

2) Построение графика функции 

3) Построение графика функции 

5.     Реализация выбранного плана. «Открытие новых знаний»

Целесообразно рассматривать построение графиков в следующей последовательности:

Построение графиков следует осуществлять двумя способами:

1.     на основании определения модуля;

2.     на основании правил (алгоритмов) геометрического преобразования графиков функций.

Построение графика функции 

Следовательно, график функции  состоит из двух графиков:  - в правой полуплоскости, - в левой полуплоскости.

Исходя из этого, можно сформулировать правило (алгоритм).

График функции  получается из графика функции  следующим образом: при x0 график сохраняется, а при x<0 часть графика в правой полуплоскости отображается симметрично относительно оси Oy.

Построение графика функции 

Отсюда вытекает алгоритм построения графиков функции .

а) Строим график функции f(x).

б) Часть графика, лежащая над осью Ox, сохраняется, часть его, лежащая под осью Ox, отображается симметрично относительно оси Ox.

Построение графика функции 

Правило (алгоритм) построения.

Чтобы построить график функции , надо сначала построить график функции y=f(x) при x>0, затем при x<0 построить изображение, симметричное ему относительно оси Oy, а затем на интервалах, где , построить изображение, симметричное графику относительно оси Ox.

6.     Первичное закрепление новых знаний

 (построение графиков функций на примерах)

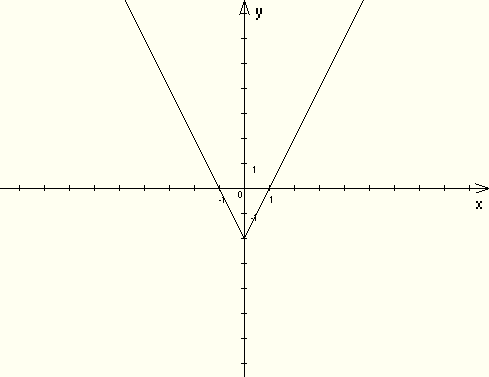
Пример 1.

Построить график функции 

Построение.

1-й способ.

Построим, опираясь на определение модуля действительного числа.

2-й способ.

Построим, используя способы преобразования графика функции.

а) Строим график функции  для x>0.

б) Достраиваем его левую часть для x<0, симметрично построенной относительно оси Oy.

Пример 2.

Построить график функции 

Построение.

1-й способ.

Строим график кусочной функции по определению модуля.

2-й способ.

Строим на основе преобразования графика уже известной нам функции.

а) Строим график функции y=x-2.

б) График нижней полуплоскости отображаем вверх симметрично относительно оси Ox.

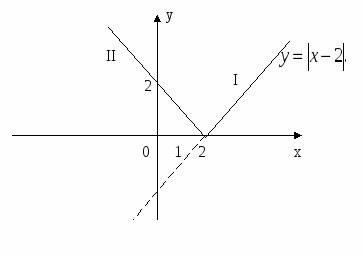
Пример 3.

Построить график функции .

Построение.

1-й способ.

Построим на основе определения модуля действительного числа.

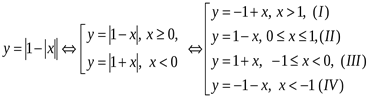
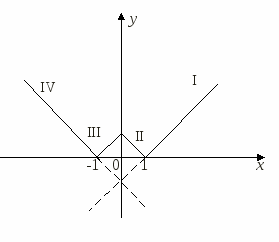
2-й способ.

Построим на основе простейших способов преобразования графика функции.

1) Строим график функции .

2) График функции , получаем из графика функции  отражением симметрично (при ) относительно оси Oy.

3) График функции , получаем из графика функции отображением симметрично оси Ox нижней части графика.

7.     Включение в систему знаний и умений

(построение графиков, задание – установи соответствие)

1. Начнем с построения графика

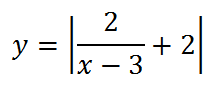
В “основе” его лежит график функции

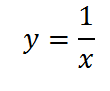
и все мы знаем, как он выглядит:

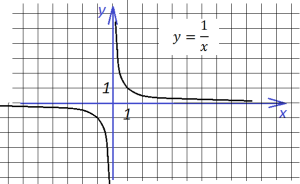
Теперь построим график

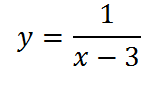
Чтобы получить этот график, достаточно всего лишь сдвинуть полученный ранее график на три единицы вправо. Заметим, что, если бы в знаменателе дроби стояло бы выражение х+3, то мы сдвинули бы график влево:

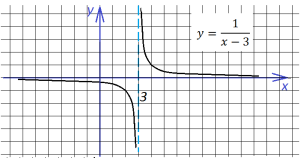
Теперь необходимо умножить на два все ординаты, чтобы получить график функции

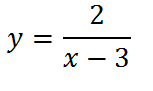
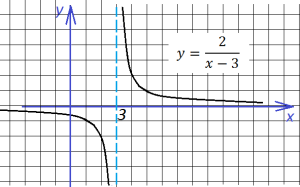
Наконец, сдвигаем график вверх на две единицы:

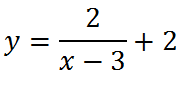
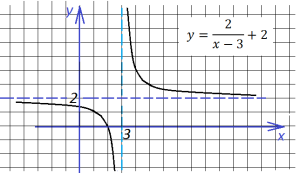
Последнее, что нам осталось сделать, это построить график данной функции, если она заключена под знак модуля. Для этого отражаем симметрично вверх всю часть графика, ординаты которой отрицательны (ту часть, что лежит ниже оси х):

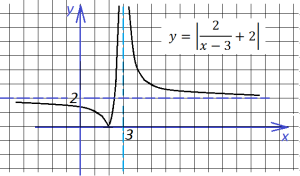
2. Теперь построим график функции

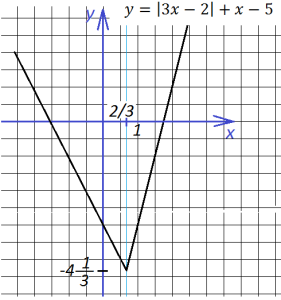
Выражение, стоящее под знаком модуля, меняет знак в точке х=2/3.

При х<2/3 функция запишется так:

При х>2/3 функция запишется так:

То есть точка х=2/3 делит нашу координатную плоскость на две области, в одной из которых (правее) мы строим функцию

а в другой (левее) – график функции

Строим:

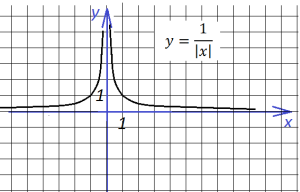
3. Теперь можем построить  график, похожий на один из предыдущих, и все же отличающийся:

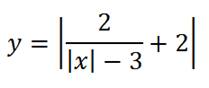
В основе опять знакомый нам график функции

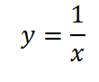
но, если в знаменателе x стоит под знаком модуля,

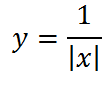
то график имеет вид:

Теперь произведем сдвиг на три единицы,

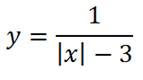
 при этом сдвинутся обе части: правая – вправо, левая – влево (своеобразное зеркало : отходишь дальше – видно больше)

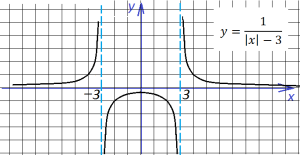
График этой функции, умноженной на два,

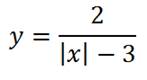
выглядит так:

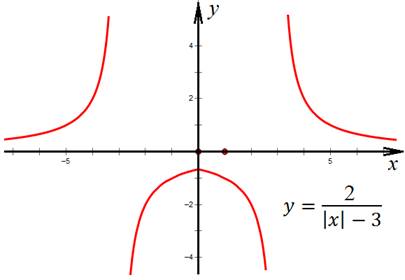
Теперь можно поднять график по оси у:

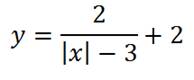
и тогда он будет таким: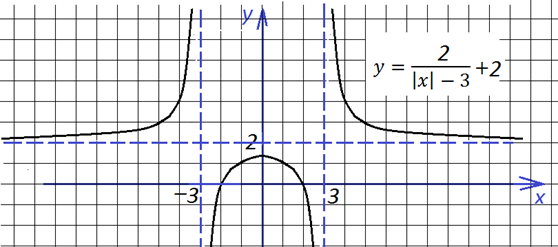

Наконец, строим окончательный вид графика, отражая все, что ниже оси абсцисс, вверх:

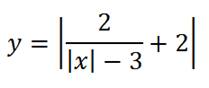
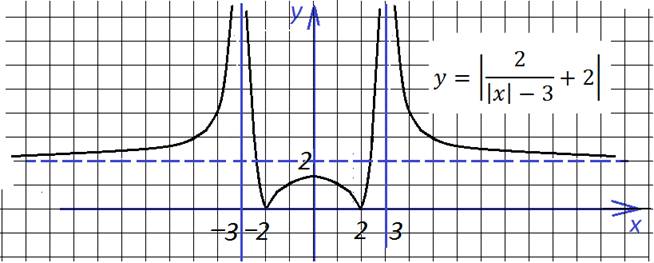
Очень интересно выглядит график функции

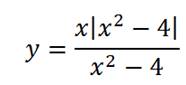
В точках 2 и (-2) знак подмодульного выражения меняет знак, поэтому функция состоит из трех кусков (точки 2 и (-2) выколоты). На участках  (-∞; -2) и (2; ∞) справедливо первое уравнение, а на участке (-2;2) – второе:

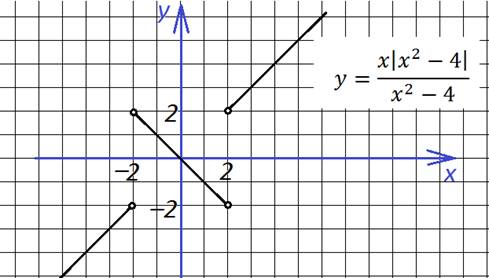
Установите соответствие между функцией и графиком функций, содержащих модуль.

1.     y = |x² – 8|x| + 12|

2.     y = x² – 8|x| + 12.

3.     y = |x² – 8x + 12|.

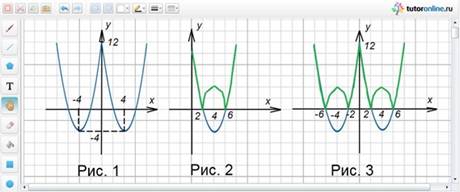
Ответы:

Пример 1.

y = x² – 8|x| + 12.

Решение.

Определим четность функции. Значение для y(-x) совпадает со значением для y(x), поэтому данная функция четная. Тогда ее график симметричен относительно оси Oy. Строим график функции y = x² – 8x + 12 для x ≥ 0 и симметрично отображаем график относительно Oyдля отрицательных x (рис. 1).

Пример 2.

y = |x² – 8x + 12|.

– Какова область значений предложенной функции? (y ≥ 0).

– Как расположен график? (Над осью абсцисс или касаясь ее).

Это значит, что график функции получают следующим образом: строят график функции y = x² – 8x + 12, оставляют часть графика, которая лежит над осью Ox, без изменений, а часть графика, которая лежит под осью абсцисс, симметрично отображают относительно оси Ox (рис. 2).

Пример 3.

y = |x² – 8|x| + 12|

Для построения графика функции y = |x² – 8|x| + 12| проводят комбинацию преобразований:

y = x² – 8x + 12 → y = x² – 8|x| + 12 → y = |x² – 8|x| + 12|. 

Ответ: рисунок 3.

8.     Рефлексия, самоанализ, выставление оценок, домашнее задание, рефлексия чувств и эмоций.

Выводы:

1.     Модуль — это не просто две палочки, а жизнерадостное, всегда положительное значение!

2.     Модулю без разницы находится он в прямой, параболе или еще где-то. Отражения происходят одни и те же.

3.     Любой нестандартный модуль можно разбить на кусочно-заданные функции, условия только вводятся на каждый модуль.

4.     Существует большое количество модулей, но парочку вариантов стоит запомнить, чтобы не строить по точкам:

• Если модуль «надет» на все выражение (например, y = |x² + x − 2|), то нижняя часть отражается наверх.
• Если модуль «надет» только на х (например, y = x² + |x| − 2), то правая часть графика отражается на левую часть. А «старая» левая часть стирается.
• Если модуль «надет» и на х, и на все выражение (например, y = |x² + |x| − 2|), то сначала отражаем график снизу вверх, после этого стираем полностью левую часть и отражаем справа налево.
• Если модуль «надет» на y (например, |y| = x² + x − 2), то мы оставляем верхнюю часть графика, нижнюю стираем. А после отражаем сверху вниз.

Ответы:

Математический диктант

Устная работа с таблицей

Необходимо указать номера примеров, где есть ошибка (истинно/ложно)

Установите соответствие между функцией и графиком функций, содержащих модуль.

12-13правильных ответов – 5

10-11 правильных ответов -4

7-9 правильных ответов – 3

Меньше 7 ответов – очень плохо! Учи!!!

Оценка _________

Индивидуальная карточка учащегося  _____ класса                дата ________

Фамилия, имя  ___________________________________

 Математический диктант

Ответы:

Устная работа с таблицей

Необходимо указать номера примеров, где есть ошибка (истинно/ложно)

Ответы:

Установите соответствие между функцией и графиком функций, содержащих модуль.

1.     y = |x² – 8|x| + 12|

2.     y = x² – 8|x| + 12.

3.     y = |x² – 8x + 12|.

12-13правильных ответов – 5

10-11 правильных ответов -4

7-9 правильных ответов – 3

Меньше 7 ответов – очень плохо! Учи!!!

Оценка _________

Скачано с www.znanio.ru