РАЗРАБОТКА КРУЖКА «МАТЕМАТИКА В ИГРЕ»

Математические игры и головоломки очень популярны, как, впрочем, и все игры. И далеко не всегда более сложная игра – более интересная. Часто миллионы людей с огромным интересом играют в самые простые игры, и именно эти игры больше всего ценят, именно они входят в историю математики и прославляют своих создателей.

Наиболее приближенными к математике являются головоломки, но много головоломок образовалось из, когда–то существовавших игр. Большинство таких основополагающих игр было придумано древнегреческими математиками.

В последнее время математическим играм внимание уделяется, в основном, для нахождения выигрышных стратегий, на что сильно повлияло распространение программирования: составить алгоритм, по которому в игру смог бы играть компьютер, часто бывает сложнее и интереснее, нежели самому научиться играть в неё, при этом глубже вникаешь в суть игры, после чего выиграть в неё можешь уже практически любого.

Простейшие математические игры часто используют как задачи, в которых нужно найти выигрышную стратегию, либо одно положение перевести в другое. Иногда задачи бывают весьма простыми, когда они решаются известными методами, такими как инвариант и раскраска, но есть и весьма простые, но до сих пор неразрешённые задачи, связанные с математическими играми.

 

 

 

 

 

 

§1 Программа кружка по математике для учащихся 7-х классов

«Математика в игре»

1.1. Пояснительная записка

С целью формирования устойчивого интереса к математике, а также активизации мыслительной деятельности учащихся составлена программа кружка «Математика в игре».

Программа кружка по математике составлена для учащихся 7–х классов, проявляющих высокий интерес к математике. В результате занятий учащиеся должны приобрести навыки и умения решать разнообразные задачи, и научиться использовать математические задачи для моделирования игр. Также ученики должны понять, что игры не только развлечение и найти взаимосвязь между игрой и математикой.

Программа кружка «Математика в игре», рассчитана на 1 час в неделю.  Она реализует требования государственных стандартов по математике, значительно углубляет их, дополняет разнообразием математических задач, непосредственно связанных с игровой деятельностью.

Задачи кружка:

ü  расширить и углубить знания по предмету в соответствии с интересами и склонностями учащихся;

ü  познакомить учащихся с историей возникновения математики на примере игр;

ü  развить познавательную и творческую активность учащихся;

ü  рассмотреть с учащимися некоторые методы решения арифметических и логических задач;

ü  воспитать настойчивость, инициативу;

ü  развить коммуникативные навыки путем включения школьников в различные виды деятельности.

Ведущие принципы:

1.      Содержание и структура программы рассматривается как особая дидактическая конструкция, создаваемая с учетом возрастных особенностей учащихся (психофизических интересов, склонностей);

2.      В основу содержания и структуры программы положен дидактический принцип личностно-ориентированного обучения, в качестве главного объекта учебно-воспитательного процесса рассматривающий учащегося с его индивидуальными особенностями восприятия и осмысления;

3.      Принцип компетентностного подхода, т.е. конечный результат обучения определяется не столько суммой приобретенных знаний, сколько умением применять их на практике, в повседневной жизни, использовать для развития чувственных, волевых, интеллектуальных и других качеств личности учащегося.

1.2. Рекомендации к организации кружка

Примерная структура занятия:

1.      Объяснение учителя и доклад «чтецов» по теме занятия.

2.      Разбор задач по теме занятия. После решения первой задачи всеми или большинством учащихся один из учащихся производит ее разбор. Учитель по ходу решения задач формулирует выводы, делает обобщения.

3.      Разбор игр и перевод их на язык математики происходит с помощью учителя и самостоятельно.

4.      Подведение итогов занятия (ответы на вопросы учащихся, обсуждение следующей встречи, домашнее задание).

При закреплении материала, совершенствовании знаний, умений и навыков целесообразно практиковать самостоятельную работу школьников. На занятиях кружка можно использовать различные современные образовательные технологии и сочетать все режимы работы: индивидуальный, парный, групповой, коллективный.

На первом занятии кружка надо наметить основное содержание работы, выбрать старосту кружка, договориться с учащимися о правах и обязанностях членов кружка, составить план работы и распределить поручения за те или иные мероприятия (выпуск математической стенной газеты, ведение документации работы кружка и т. п.).

Занятия кружка целесообразно проводить один раз в неделю, выделяя на каждое занятие по одному часу. К организации работы математического кружка целесообразно привлекать самих учащихся, поэтому на каждом уроке учитель выбирает несколько учеников (в дальнейшем «чтецы»), которым будет поручена подготовка небольших сообщений об основных математиках, чьи игры и задачи будут разбираться на занятии.

На занятиях математического кружка учитель должен создать "атмосферу" свободного обмена мнениями и активной дискуссии, поскольку разбор игр, даже со стороны математики, содержит в себе игровые моменты.

Изложение теоретического материала кружковых занятий должно осуществляться преимущественно с использованием активных методов обучения. В зависимости от цели и типа занятия используются различные формы работы, такие как групповые, парные, командные, индивидуальные. Ведущее место при проведении занятий должно быть уделено задачам, развивающим познавательную и творческую активность учащихся.

Основной тип занятий: комбинированный.

Система занятий должна вести к формированию следующих характеристик творческих способностей:

·         беглость мысли,

·         гибкость ума,

·         оригинальность,

·         любознательность,

·         умение выдвигать и разрабатывать гипотезы.

Для эффективной организации курса используются различные формы проведения занятий:

·         эвристическая беседа,

·         практикум,

·         интеллектуальная игра,

·         дискуссия,

·         творческая работа.

Таким образом, программа кружка «Математика в игре», отвечая предметным, метапредметным и личностным целям обучения, имея большую информационную насыщенность, даёт возможность учащимся значительно расширить математический кругозор, повысить глубину усвоения программы основного курса математики 7 класса, приобрести устойчивый интерес к изучению математики.

Кружок имеет и пропедевтическую направленность, его изучение позволит учащимся сформировать представления о своих возможностях в области математики.

Содержание программы может изменяться, расширяться или углубляться в рамках тем, выбранных для самостоятельного изучения. Программа может содержать разные уровни сложности изучаемого материала и позволяет найти оптимальный вариант работы для определенной группы учащихся, ее можно расширять, изменять с учетом конкретных педагогических задач и запросов детей.

 

 

1.3. Календарно – тематическое планирование кружка

 «Математика в игре»

№ Занятия	Тема занятия	Кол-во часов
Раздел 1: «Взаимосвязь математики и игр». История математики.
1	Наша жизнь и математика. Наша жизнь и игры. История взаимосвязи игр и математики до XVIIв во времена Античности. Задачи: Папирус Ахмеса; Игра сенет; Игры урских царей.	1
2	Игры и математика в Средневековье и эпохе Возрождения. Задачи: Числа Фибоначчи и его задача о квадратах; Легенда об изобретении шахмат; Игра Алькерк Задачи Тарталья Задачи Шюке	1
3	Турнир Математиков	1
4	Игры и математика с XVII века до наших дней. Золотой век математики. Задачи: Задачи из книги Мезириака; Задачи Ньютона о корове, и кубиках; Задачи Эйлера о магическом квадрате; Задача о кёнигсбергских мостах; Задача о 8 ферзях; Парадокс Хупера.	1
5,6	Игры и занимательная математика XIX и XX веках. Задачи: Задачи Льюиса Кэрролла; Задачи Эдуарду Люка; Задачи Генри Эрнест Дьюдени; Задачи Сэма Лойда; Игра Роберта Эббота; Задача о костяшках домино Якова Перельмана.	1
Раздел 2: «Стратегические игры». Алгебраические задачи.
7,8	Классификация игр.  Определение выигрышной стратегии. Задачи: НИМ; Вращаем кубик; Разрезаем прямоугольник; Пересекаем круг; Цзяньшицзу; Маргаритка.	2
9	Псевдоигры. Задачи: Нечетные фишки; Ряд фигур; Замкнуть треугольник; Плитка шоколада.	1
10	Турнир математиков	1
Раздел 3: «Азартные игры». Теория вероятности.
11	Игры и азарт. Задачи: Разделение ставок; Победители забега; Бридж;	1
12	Турнир математиков.	1
Раздел 4: «Современные игры». Подводим итоги.
13,14	Разбор современных игр с точки зрения математики.	2
Итого		14 часов

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

§2 Принципы отбора содержания

При разработке кружка, нельзя забывать о месте и роли его в процессе обучения школьников. Мы не должны забывать, что кружок должен дополнять и опираться на знания школьников, поэтому мы следовали некоторым принципам при отборе содержания:

1.      Принцип связи программы школьного курса математики 7 класса с программой кружка.

2.      Принцип взаимосвязи и пропедевтики изучения новых вопросов программы школьного курса.

3.      Принцип связи с историей и жизнью.

4.      Принцип формирования познавательного интереса.

5.      Принцип доступности и наглядности.

Рассмотрим применение этих принципов подробнее.

Принцип связи программы школьного курса математики 7 класса с программой кружка.

Отбирая материал из различных источников, мы руководствовались тем, может ли этот вопрос стоять при изучении школьного курса математики в 7 классе [1,17,18].  Анализ программы по математике и учебников показал, что, не нарушая логики, мы можем включить в программу кружка следующие вопросы:

·         Математические модели реальных ситуаций;

·         Решение задач с помощью уравнений;

·         Числовые последовательности;

·         Признаки делимости;

 

 

Принцип взаимосвязи и пропедевтики изучения новых вопросов программы школьного курса.

В разделе 3, при разборе азартных игр, ученики занимаются теорией вероятности. В новой программе, начиная с 5 и 6 класса, рассматриваются начала комбинаторики, перестановки [5]. Это позволило нам включить в программу задачи, основывающиеся на понятии и свойствах вероятностей, и для решения которых, нужно знать о перестановках, сочетаниях, размещения.

Одна из линий учебников, в которых последовательно с 5 по 9 класс проводится вероятностно-статистическая линия, органично и системно связанная с другими темами курса - это новый учебный комплект «Математика 5-6» по ред. Г.В. Дорофеева и И.Ф. Шарыгина, «Математика 7-9» под ред. Г.В. Дорофеева, а также в сборнике И.Л Гусевой "Тестовые материалы для оценки качества обучения", предназначенном для оценки качества обучения учащихся по математике в 6 классе, имеется раздел, посвящённый комбинаторике [1,7,13,19].

Принцип связи с историей и жизнью.

Ученики, изучая математику не должны забывать о её исторических началах, мы считаем необходимым включение в программу задач, которые будут показывать ученикам связь математики и их жизни, жизни наших предков. Именно этому посвящен Раздел 1 разработанного кружка. В нем ученики слушают историю взаимосвязи математики и игр, делают мини-доклады о выдающихся математиках, ищут взаимосвязи в играх современных и давних времен [10, 14, 25]

Принцип формирования познавательного интереса.

При отборе содержания мы учитывали, что кружок — это не только углубление теоретических знаний, закрепление практических умений и навыков по предмету, но и развитие творческих способностей учащихся, формирование познавательного интереса, организация досуга учащихся. В связи с этим мы посчитали необходимым включить в программу уроки - «турнир математиков». На данных уроках, ученики смогут побороться за лидерство, что немаловажно в их возрасте, а также они покажут умения, которые приобрели на занятиях.

Принцип доступности и наглядности.

Сохранение интереса к изучению математики при использовании новых комплектов учебников обеспечивается не только через дополнительные темы, но и через достаточное количество занимательных задач.

Занимательные задачи — инструмент для развития мышления, ведущего к формированию творческой деятельности школьника. К таким задачам относятся задачи «на соображение», «на догадку», головоломки, нестандартные задачи, логические задачи, творческие задачи.

При работе над вопросом задачи главное и наиболее трудное для ученика – определить, в какой связи эта искомая величина находится с данными, в задаче или игре, величинами.

Сначала учащийся анализируют конкретное содержание задачи, о чем говорится в ней, о каких фактах или явлениях, в какой последовательности они происходят. Читая и перечитывая условие, они выделяют из него данные, стараются уловить те связи, которые существуют между данными в задаче. Чтобы облегчить анализ условия задачи, их лучше наглядно представить в виде чертежа, рисунка или схемы. Это облегчает решение задачи, делает его более убедительным и доказательным.

Учитывая этот принцип, мы включили в программу игры и задачи, решая которые, ученику придется наглядно представить ее, или даже сыграть самому.

 

 

§3 Содержание кружка «Математика в игре»

Раздел 1: «Взаимосвязь математики и игр»

Занятие 1. «Наша жизнь и математика. Наша жизнь и игры. История взаимосвязи игр и математики во времена Античности»

Цель: познакомить учащихся с историей математики на примере взаимосвязи математики и игр, вспомнить составление математической модели реальных ситуаций и различные формы работы с дробями.

Форма проведения занятия: Комбинированное занятие: эвристическая беседа, практическая работа

Ход занятия:

1. Сообщение темы и цели урока.

2. Изучение нового материала.

Первое, что необходимо сделать на занятии, это провести обсуждение на темы: «Где математика встречается в вашей жизни? Где игра встречается в вашей жизни? Какова взаимосвязь между играми и математикой? Игры - это всего лишь развлечение, или же их можно использовать для моделирования реальных событий? Что нужно знать для анализа игры? Можно ли использовать математику в реальной жизни, чтобы анализировать поведение человека и при принятии решений?» 

Необходимо обсудить роль математики в науке, жизни, обществе, выдвинуть гипотезу, что развлекательный характер множества игр не означает, что они не требуют математических вычислений, напротив, тот кто лучше проведет нужные расчеты, тот и одержит победу.

Здесь, необходимо убедиться с учениками, что процесс обдумывания ходов в играх очень похож на решение математических задач, так как математика сама по себе может быть занимательной и стимулировать интеллект.

Далее, после установки взаимосвязи данных понятий, можно приступить к изучению непосредственно истории математики и игр. В первом разделе группа совершит краткий экскурс в историю математики с древнейших времен до наших дней, чтобы убедиться, что развлечениям для ума находилось место и в древности.

С древнейших времен история математики полна упоминаний об играх и занимательных задачах. В действительности с момента появления игр, параллельно ей появилась и развивалась математика. С этих времен серьезную и занимательную математику нельзя было отделить друг от друга.

В великих цивилизациях древности Вавилоне и Египте несмотря на то, что математика носила практический характер, встречаются настольные игры и занимательные задачи. В одной из древнейших рукописей мира о математике – папирусе Ахмеса (1650 года) встречаются помимо математических задач, занимательные игры.

Еще одна известная нам древнейшая игра «сенет». Задача этой игры, рассчитанной на двух игроков, - первым довести до конца доски семь фишек. Эта игра считалась игрой с судьбой, от которой зависела дальнейшая загробная жизнь.

3. Задачи для решения:

1) Египетская задача.

Египетский фараон Тутмос был широко известен своими завоевательными походами. Однажды среди трофеев у него оказалось 2000 золотых монет: больших, средних и маленьких. Большие монеты составили 35% от общего числа монет, а средние монеты - 17/20 от числа больших монет. Сколько было маленьких монет? Каких монет у Тутмоса оказалось больше - маленьких или больших, и на сколько?

 

2) Задача о быках.

Приходит пастух с 70 быками. Его спрашивают: - Сколько приводишь ты своего многочисленного стада? Пастух отвечает: - Я привожу две трети от трети скота. Сочти!" Сколько быков было во всем стаде?

3) «Ученики»

Спросил некто учителя: “Сколько у тебя в классе учеников, так как я хочу отдать к тебе в учении своего сына”. Учитель ответил: “Если придет еще учеников столько же, сколько имею, и четвертая часть, и твой сын, тогда будет у меня учеников 100”. Спрашивается, сколько было у учителя учеников?

4) «Целое и седьмая его часть дают 19»

Поскольку в 7 классе ученики уже умеют работать с математической моделью реальных ситуаций, то они смогут перевести задачи Ахмеса на язык математики. Помимо работы с математической моделью, ученики вспомнят правила работы с дробями и сравнят современные методы с методами Древнего Египта.

Занятия можно дополнить выступлениями из истории математики в Древнем Египте.

4. Домашнее задание: Чтецам подготовить выступления на 2-3 минуты о:

Леонардо Пизанском (Фибоначчи), Ибн-Халликана, Никколо Фонтана (Тарталья), Джероламо Кардано.

 

 Занятие 2. «Игры и математика в Средневековье и эпохе Возрождения»

Цель: познакомить учащихся с историей математики в Средневековье и эпохе Возрождения, и изучить древние задачи, повторить свойства степеней и правила работы с ними.

Форма проведения занятия: Комбинированное занятие: Эвристическая беседа, мини-доклады учащихся, практическая работа

Ход занятия:

1.      Сообщение темы.

2.      Изучение новой темы.

Мы познакомились с наиболее интересными фактами из древней истории взаимоотношений игр и математики, а теперь перенесемся в XIII век. Именно тогда жили Леонардо Пизанский (Фибоначчи), Ибн-Халликан (легенда об изобретении шахмат). Математику эпохи Возрождения представляют главным образом итальянские алгебраисты, которые занимались в основном решением уравнений. Предоставим несколько минут нашим чтецам.

Фибоначчи является автором «Книги квадратов», где описал математический турнир, проводимый в подлинно средневековом стиле, где каждый участник, должен был предложить сопернику определенное количество задач. Победителем турнира был тот, кто решит больше задач, за меньшее время. При этом участник предложивший задачу, должен был знать ее решение.

3.      Задачи (из турнира):

1)      Задача Фибоначчи:

Нужно найти такое число, что если прибавить или вычесть из его квадрата 5, то в обоих случаях результатами также будут квадраты.

2)      Задача Ибн-Халликана:

Из легенды об изобретении шахмат: Сколько зерен должен был бы положить

Ширхам на шахматную доску, если просьбой Сисса бен Дахира было положить пшеничное зернышко на первую клетку доски, 2-на вторую, 4-на третью, 8-на четвертую и так далее до 64 клетки, каждый раз удваивая число зерен. Смог бы выполнить эту просьбу индийский король Ширхам?

3)      Задачи Тарталья:

У некого человека 17 лошадей. Он оставляет их в наследство сыновьям, завещав разделить коней между ними в пропорции ½, 1/3, 1/9. Как сыновьям поделить наследство?

4)      Задача Николя Шюке:

Даны два сосуда. Один вмещает 3 пинты, второй -  5. Как отмерить ровно 4 пинты с помощью переливаний? На сосудах нет отметок.

5)      Игра Алькерк:

Алькерк - игра двух игроков, описанная в «Книге игр» Альфонсо Х Мудрого. Доска имеет размеры 5 на 5 клеток, у каждого игрока 12 фишек, они распологаются так, что центральная клетка-свободная. Цель игры- убрать с доски все фишки соперника.

 

 

4.      Домашнее задание:

Подумать над задачей Тарталья: У некого человека три фазана. Он хочет разделить их между двумя отцами и двумя сыновьями так, чтобы каждому из них достался фазан. Как это сделать?

Подготовить 2 задачи, для математического турнира, на подобие тех, которые видели.

Занятие 3. Турнир математиков.

1.      Форма проведения занятия: Интеллектуальная игра

2.      Цели игры:

·         Развитие познавательного интереса к предмету математика, применение математических знаний во внеурочной обстановке.

·         Развитие у учащихся познавательного интереса и любознательности.

·         Воспитание доброжелательности, инициативности, активности.

3. Ход проведения занятия:

1) Представление команд. За представление командам засчитывается до 4 баллов.

2) Разминка. Для рассмотрения предлагается следующие задачи:

    1. Найдите закономерность: 2, 4, 8, 64, ….

За найденную закономерность команде засчитывается 1 балл.

   2. У семи лиц по семи кошек, каждая кошка съедает по семи мышей, каждая мышь съедает по семи колосьев ячменя, из каждого колоса может вырасти по семи мер зерна. Сколько мер зерна сохраняется благодаря этим кошкам? (Египетский папирус – около 2000лет до н.э.)   (16 807 мер)

     3. Наполненный доверху водой сосуд имеет массу 5 кг, а заполненный наполовину – 3 кг 500 г. Сколько воды вмещает сосуд? (3 кг воды)

Правильное решение задач – 5 баллов.

3) Проверка домашнего задания. Оценивается в 5 баллов.

4) Турнир начинается:

Из каждой команды, выходят по 1 человеку, со своими задачами, и загадывают по очереди их противнику. За выигрыш каждого команда получает 1 балл. Все задания выполняются своевременно, затем происходит отчет.

Подсчитывается итоговый результат и определяется победитель, награждаются обе команды грамотами: за победу и за участие.

Занятие 4. Игры и математика с XVII века до наших дней. Золотой век математических игр.

Цель: познакомить учащихся с золотым веком математических игр, решить известные исторические задачи.

Форма проведения занятия: Комбинированное занятие: Эвристическая беседа, мини-доклады учащихся, практическая работа

Ход занятия:

1. Сообщение темы и цели урока.

2. Изучение нового материала.

Серьезная и занимательная математика существовали с древнейших времен вместе, и в ХVII веке появляется особое ответвление, посвящённое играм. Книга де Мезириака – своеобразный конспект по занимательной математике той эпохи.  (Выступления чтецов.)

3. Задачи:

1) Задачи из книги Мезириака:

 

·         Задача о козе, волке, и капусте.

Крестьянину нужно перевезти через реку волка, козу и капусту. Но лодка такова, что в ней может поместиться только крестьянин, а с ним или один волк, или одна коза, или одна капуста. Но если оставить волка с козой, то волк съест козу, а если оставить козу с капустой, то коза съест капусту. Как перевез свой груз крестьянин?

·         Задача о гирях.

Найти минимальное число гирь и их массу, с помощью которых на простых весах с двумя чашками можно измерить любой вес, выраженный целым числом от 1 до 40.  

2) Задачи Ньютона:

Трава на лугу растёт одинаково густо и быстро. Известно, что 70 коров съели бы всю траву за 24 дня, а 30 коров – за 60 дней. Сколько коров съест всю траву на лугу за 96 дней?

·         Вероятность какого из следующих событий наибольшая?

1.При броске 6 кубиков выпадет хотя бы одна шестерка.

2.При броске 12 кубиков выпадут хотя бы две шестерки.

3.При броске 18 кубиков выпадут хотя бы три шестерки.

 

3) Задачи Эйлера:

·         Прообраз судоку

Расположить n символов в квадрате n на n клеток так, чтобы в каждой строке и в каждом столбце находились все возможные символы.

 

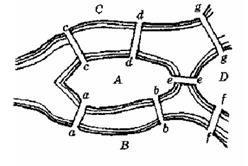
·         Задача о кёнигсбергских мостах:

Можно ли обойти все семь мостов, стоявших тогда в городе Кёнигсберге, побывав на каждом по одному разу?

4) Задача Гаусса:

Расставить на стандартной 64-клеточной шахматной доске 8 ферзей так, чтобы ни один из них не находился под боем другого.

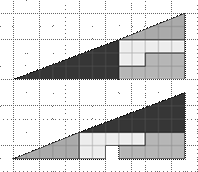
1)      Парадоксы Хупера (рекомендовано показать наглядно)

·         Задача о треугольнике

Дан прямоугольный треугольник 13×5 клеток, составленный из 4 частей. После перестановки частей при визуальном сохранении изначальных пропорций появляется дополнительная, не занятая ни одной частью, клетка).

·         Задача о квадрате:

Большой квадрат составлен из четырёх одинаковых четырёхугольников и маленького квадрата. Если четырёхугольники развернуть, то они заполнят площадь, занимаемую маленьким квадратом, хотя площадь большого квадрата визуально не изменится. При следующем развороте маленький квадрат появится снова.

 

 

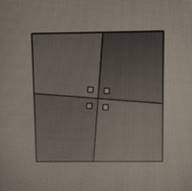
4. Домашнее задание:

Чтецам подготовить рассказы о Льюисе Кэрролл, Эдуарду Люка.

Занятие 5,6. Игры и занимательная математика XIX и XX веках.

Цель: познакомить учащихся с математикой XIX-XX вв, решить известные исторические задачи.

Форма проведения занятия: Комбинированное занятие: Эвристическая беседа, мини-доклады учащихся, практическая работа

Ход занятия:

1. Сообщение темы и цели урока.

2. Изучение нового материала.

Игры и занимательная математика в ХIX-XX веках начали бурно развиваться, и в эти века было очень много достижений, о которых невозможно рассказать в рамках курса, однако мы с вами остановимся на самых интересных персонажах этого времени. (выступление чтецов)

3.Задачи:

1) Задачи Льюиса Кэролл:

·         Часы.

Есть двое часов. Одни стоят, другие опаздывают на одну минуту. Какие часы показывают время точнее?

·         Лестница слов.

 Как превратить козу в волка?

  (КОЗА-ПОЗА-ПОЛА-ПОЛК-ВОЛК)

 

2) Задачи Эдуарда Люка:

·         Ханойские башни.

Ханойская башня является одной из популярных головоломок XIX века. Даны три стержня, на один из которых нанизаны восемь колец, причем кольца отличаются размером и лежат меньшее на большем. Перенесите пирамиду из восьми колец за наименьшее число ходов на другой стержень, при условии, что за один раз разрешается переносить только одно кольцо, причём нельзя класть большее кольцо на меньшее.

·         «Французские военные игры»

Игра рассчитана на двух игроков, у одного 3 белые фишки, у другого –одна черная. Первым ходит тот, у кого черная фишка. Фишки располагаются на доске из 11 клеток. Задача белых фишек- окружить черную, которая пытается сбежать. Черные фишки могут двигаться в любом направлении, а белые не могут отступать назад.  Каково минимальное число ходов вам потребуется, чтобы выиграть?

3) Задачи Генри Эрнест Дьюдени:

·         Задача галантерейщика

Необходимо разрезать равносторонний треугольник на 4 части и составить из них квадрат.

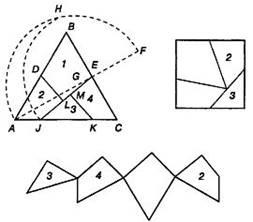
·         Криптарифмы:

РЕШИ+ЕСЛИ=СИЛЕН

Нужно заменить буквы цифрами так, чтобы получилось верное равенство. Причем в числе СИЛЕН наибольшая цифра не превышает

         4) Задача Сэма Лойда:

Задача о соединении 9 точек, расположенных в форме квадрата 3 на 3, четырьмя прямыми линиями, не отрывая карандаша от бумаги.

Расположите числа от 1 до 8 в вершинах куба так, чтобы сумма чисел на каждых четырех вершинах одной грани была одинаковой.

5) Задача Якова Перельмана:

Четыре костяшки домино расположены в виде квадрата так, что суммы чисел на его сторонах равны. Задача – составить семь таких квадратов из полного набора домино.

Некоторые задачи могут использоваться в качестве домашнего задания.

4. Домашнее задание:

1) Задача о соединении 16 точек, расположенных в форме квадрата 4 на 4, четырьмя прямыми линиями, не отрывая карандаша от бумаги.

 

2) Придумать задачу, аналогичную задаче галантерейщика Генри Эрнест Дьюдени

3) Чтецам: рассказать о происхождении игры НИМ (2-3 минуты).

Раздел 2 «Стратегические игры».

Занятие 7.  Классификация игр.  Определение выигрышной стратегии.

Цель: познакомить учащихся с классификацией игр, ввести понятие выигрышной стратегии.

Форма проведения занятия: Комбинированное занятие: Эвристическая беседа, мини-доклады учащихся, практическая работа

Ход занятия:

1. Сообщение темы и цели урока.

2. Изучение нового материала.

Игра может обозначать как собственно игру, в которой участвует несколько игроков, так и математические развлечения, и головоломки. Мы будем говорить об играх, в которых имеется как минимум два игрока. Цель игры-одержать победу в партии.

Применительно к математике игры можно разделить на две группы в зависимости от того, присутствуют в них элемент неопределенности или нет. Стратегическими будем называть игры с полной информацией, а азартными игры, где присутствует элемент неопределенности.

После изучения правил и сути игры, люди обычно задаются вопросом: какие ходы надо совершать, чтобы одержать победу? В азартных играх, такой вопрос не будет актуален, поскольку все зависит от случая, а не от игроков, поэтому путь выигрыша определить невозможно, тогда как в стратегических играх, в любой момент можно узнать все возможные ходы и их последствия.

Рассмотрим для начала стратегические игры, поскольку в стратегических играх выигрыш зависит от игроков, то введем понятие выигрышной стратегии. Выигрышная стратегия-множество условий, позволяющих одному из игроков определить, как следует действовать, чтобы одержать победу.

Рассмотрим свойства стратегической игры:

1)      Все игроки обладают информацией, которая позволит определить следующий выигрышный ход;

2)      Игроки совершают ходы поочередно;

3)      Нет элемента неопределенности;

4)      Любая игра оканчивается победой одного из игроков, после числа конечного числа ходов.

(Стоит обсудить с учениками ряд проблем, возникающих при решении задач и привести примеры стратегических и азартных игр.)

Стратегические игры можно разделить также на 2 группы. Первая группа включает в себя игры, которые описываются простыми правилами и длятся достаточно короткое время, поскольку количество информации их сравнительное не велико. Вторая группа включает в себя игры, которые длятся большее количество времени, имеют сложные правила и множество вариантов возможных ходов.

На примере первой группы мы можем рассмотреть, как математика используется в анализе игр. Процесс игры очень похож на решение задач, поэтому при определении выигрышной стратегии используются эвристические методы: способ «от обратного», предположение, что игра «решена», применение симметрии, проведение аналогии.          Приступим к рассмотрению различных игр.

 

3.      Задачи:

Игра НИМ.

Рассмотрим игру НИМ. Суть игры, заключается в том, что игроки выкладывают на стол одну или несколько групп фишек и определяют правила, по которым нужно снимать фишки со стола. Цель игры – взять последнюю фишку либо, наоборот, заставить противника взять последнюю фишку.

Проанализируем игры с одной группой фишек:

На стол выкладывается 20 фишек одного цвета. На каждом ходу один из двух игроков может брать одну или две фишки. Тот, кто берет последнюю фишку выигрывает. Какой из игроков имеет преимущество-тот, кто ходит первым, или второй участник? Как нужно играть, чтобы всегда выигрывать? Что произойдет, если изменится число фишек? Что произойдет, если мы изменим правила игры и тот, кто берет последнюю фишку, проигрывает?

Чтобы составить решение общего вида, стоит найти решение для задачи:

Пусть на столе k фишек, и каждым ходом можно брать от 1 до m фишек. (m<k). Выигрывает тот, кто забирает последнюю фишку. Для какого из игроков существует выигрышная стратегия? В чем она заключается?

4. Домашнее задание:

А) Первый игрок пишет на бумаге число от 1 до 10. Второй игрок придумывает число от 1 до 10 и записывает результат сложения этого числа с первым. На каждом ходу игрок прибавляет к общей сумме новое придуманное им число от 1 до 10. Тот игрок, который запишет трехзначное число, проигрывает. Как нужно играть чтобы выиграть? Какой из игроков имеет преимущество: тот, кто ходит первым или вторым? Что произойдет, если изменится цель или правила игры?

Б) Придумайте задачу типа НИМ.

Занятие 8.  Определение выигрышной стратегии.

Цель: продолжить знакомить учащихся с стратегическим играми.

Форма проведения занятия: Комбинированное занятие: Эвристическая беседа, мини-доклады учащихся, практическая работа

Ход занятия:

1.      Сообщение темы и цели урока.

2.      Проверка д/з.

Ученики меняются придуманными играми, решают их и проверяют.

На прошлом занятии мы разобрали классификацию игр и рассмотрели один из видов стратегических игр – игру НИМ и ее вариации. Сегодня мы познакомимся с еще более интересными стратегическими играми.

3.      Задачи:

(Разделимся на 2 группы, каждая из которых выберет по 2 человека(игроков), задача состоит в нахождении выигрышной стратегии, в итоге краткое обсуждение обеих задач)

·         Вращаем кубик (1 группа)

Игра рассчитана на двоих, сидящих за партой. Первый игрок ставит кубик на стол выбранной стороной вверх. Второй игрок поворачивает кубик на четверть оборота так, чтобы на верхней грани было другое количество очков, и прибавляет это число к первому. Затем каждый игрок вращает кубик на четверть оборота и прибавляет число очков на верхней грани к общей сумме. Тот, кто первый набирает 31 очко, выигрывает.

Какой из игроков имеет преимущество? Как нужно играть, чтобы всегда выигрывать?

 

·         Разрезаем прямоугольник (2 группа)

На листе бумаги в клетку нужно нарисовать прямоугольник размерами 17 на 15 клеток. Затем нужно пометить квадратик в нижнем правом углу. Каждый из игроков своим ходом делит прямоугольник на две части с помощью вертикальной или горизонтальной линии и удаляет ту часть прямоугольника, которая не содержит маленький отмеченный квадрат. Тот, кто не сможет разделить прямоугольник, а для этого должен остаться только отмеченный квадратик, проигрывает.

Кто из игроков имеет преимущество? Как нужно играть, чтобы всегда выигрывать?

·         Игра цзяньшицзы.

(Цзяньшицзы — китайская национальная игра. Буквальный перевод слова Цзяньшицзы — выбирание камней.)

Положив на землю две кучки камней, играющие поочередно берут камни из этих кучек, соблюдая следующие правила:

а) из одной кучки можно брать любое количество камней (даже сразу всю кучку),

б) можно брать камни одновременно из двух кучек, непременно по одинаковому количеству из каждой кучки.

Выигрывает тот, кто, соблюдая эти правила, сможет взять последний камень.

·         Маргаритка

Нарисуем маргаритку с 11 лепестками и поставим по одной фишке на каждом лепестке. На каждом ходу игрок может брать одну или две фишки, причем две фишки можно брать только с соседних лепестков. Тот, кто берет последнюю фишку, выигрывает.

4.      Домашнее задание:

Решить задачу: «Пересекаем круг». На листе бумаги нужно нарисовать окружность и обозначить на ней восемь произвольных точек. На каждом ходу игрок соединяет две точки отрезком. Он может соединить любые две точки, кроме уже соединенных, но нарисованный им отрезок не должен пересекать никакой другой отрезок. Игрок, которому не удастся провести такой отрезок проигрывает. Какой из игроков имеет преимущество? Что изменится, если изменить начальное число точек?

Занятие 9.  Псевдоигры.

Цель: познакомить учащихся с псевдоиграми, научить определять разницу между стратегическими играми и псевдоиграми.

Форма проведения занятия: Комбинированное занятие: Эвристическая беседа, мини-доклады учащихся, практическая работа

Ход занятия:

1.      Сообщение темы и цели урока.

2.      Проверка д/з      

3.      Изучение нового материала.

Мы с вами уже хорошо знаем, что представляют из себя стратегические игры, и, как нам кажется, мы сразу же сможем их определить, однако существуют такие игры, которые похожи на те, что мы с вами разбирали, но их нельзя назвать стратегическими. Выигрышную стратегию определить для псевдоигр невозможно, но можно доказать, что результаты зависят от игроков и правил. Рассмотрим псевдоигры.

4.      Задачи:

·         Нечетные фишки

На столе лежит 20 фишек. Каждый из двух игроков своим ходом может взять 1,3,5 фишек. Выигрывает тот, кто берет последнюю фишку. Какой из игроков имеет преимущество? Что произойдет если изменится число фишек? Эта игра является стратегической?

(Решив первую задачу, ученики должны прийти к выводу, что второй игрок всегда выигрывает. Выигрышную стратегию определить нельзя, поскольку игра зависит только от количества фишек и победитель заранее определен правилами игры)

·         Ряд фигур

Нарисуем в ряд несколько кругов и квадратов. Каждый игрок может:

- убрать две одинаковые фигуры и заменить их одним кругом;

- забрать две разные фигуры и заменить их одним квадратом;

В конце игры останется одна фигура, если останется квадрат выигрывает первый игрок, если круг, то второй. Существует ли выигрышная стратегия?

                        

·         Замкнуть треугольник

На листе бумаги нужно нарисовать окружность и обозначить на ней шесть произвольных точек. На каждом ходу игрок соединяет две точки отрезком, кроме тех, которые уже соединены. Игроки используют разные цвета ручки.  Тот, кто нарисует треугольник со сторонами одного цвета, выигрывает.

Какой из игроков имеет преимущество? Как нужно играть, чтобы всегда выигрывать? Что изменится, если изменить количество точек? Что произойдет если изменить правила игры?

 

·         Плитка шоколада

Плитка шоколада состоит из 28 окошек, расположенных в 4 ряда по 7 квадратиков. Первый игрок делит плитку на две части, не ломая ни одно из окошек. Второй берет одну из получившихся частей и снова делит ее. На каждом ходу игрок берет одну из двух частей и делит ее на две части. Тот, кто не сможет разделить плитку, проигрывает.

Как нужно играть чтобы выиграть? Что изменится, если плитка будет состоять из 27 окошек, расположенных в 3 ряда по 9?

5.      Домашнее задание:

1) Плитка шоколада состоит из 50 квадратных окошек, расположенных в 5 рядах по 10. Каждый игрок делит плитку вдоль вертикальной или горизонтальной линии, не ломая ни одно из окошечек. Ни одна из частей не откладывается в сторону, все они продолжают участвовать в игре. Первый игрок, который своим ходом получит одно отдельное окошко, проигрывает. Как нужно играть, чтобы выигрывать?

2) Придумать 2-3 задачи для стратегических игр для математического турнира.

Для чтецов на занятие 11: подготовить рассказ о Блезе Паскале, Пьере Ферма (на2-3 минуты), об игре Бридж.

Занятие 10.  Стратегические игры. Турнир математиков.

 Аналогично занятию 3. Турнир математиков.

Форма проведения занятия: Интеллектуальная игра

Цели:

·         Развитие познавательного интереса к предмету математика, применение математических знаний во внеурочной обстановке.

·         Развитие у учащихся познавательного интереса и любознательности.

·         Воспитание доброжелательности, инициативности, активности

Раздел 3 «Азартные игры».

Занятие 11.  Игры и азарт

Цель: познакомить учащихся с азартными играми, вспомнить элементы теории вероятности и научиться применять их в разборе азартных игр.

Форма проведения занятия: Комбинированное занятие: Эвристическая беседа, мини-доклады учащихся, практическая работа

Ход занятия:

1.      Сообщение темы и цели урока.

2.      Изучение нового материала.

Мы с вами уже говорили о классификации игр, сегодня мы с вами познакомимся с азартными играми. В этом разделе пойдет речь о взаимосвязи игр и теории вероятностей.

Во время изучения темы «Азартные игры», необходимо обсудить с учениками вред азартных игр.

В реальном мире сложные на ваш взгляд темы теории вероятности применяются в самых различных областях. Однако начало теория вероятности берет именно в азартных играх, а именно во Франции в середине XVII века. Антуан Гомбо, известный как Шевалье де Мере, посвятил большую часть своей жизни азартным играм, это, можно сказать, было его работой. Он играл в игры, где вероятность выигрыша и проигрыша одинакова, например, «нужно выбросить минимум одну шестерку броском четырех игральных костей».  Однако, Мере знал, что в этой игре один из игроков имеет преимущество, и тогда он предложил свою игру «минимум один раз выбросить две шестерки за 24 броска двух костей». Он считал, что преимущество одного из игроков будет таким же, но спустя некоторое время убедился, что все происходит наоборот. Тогда он обратился к Паскалю, чтобы тот помог ему найти ошибку в этой игре.

Вы уже знакомы с понятием вероятности, но, чтобы вспомнить, давайте решим задачи, предложенные Шевалье де Мере.

3.      Задачи:

·         Какова вероятность выбросить 6 очков минимум один раз, бросив игральные кости четыре раза?

Вам поможет: свойство вероятности - вероятность того, что произойдет некоторое событие либо обратное ему, равна 1. И вероятность события рассчитывается по правилу: p(события) = число благоприятных исходов/ общее число исходов.

·         Какова вероятность выпадения двух шестерок при броске пары кубиков 24 раза?

Рекомендуется повторить с учениками основы комбинаторики и составить таблицу свойств на примере игры в кости, где будет описываться событие и его вероятность.

·         Задача о разделении ставок.

Двое мужчин играют в игру, выигрывает тот, кто первым наберет 10 очков. В каждом раунде оба имеют равные шансы на победу. Победитель раунда получает 1 очко. После 17ой партии один из игроков выигрывает со счетом 9:8, после чего игра прекращается. Так как никто не набрал 10 очков, игроки решают разделить выигрыш. Как справедливо разделить выигрыш между игроками?

·         Забег.

В забеге участвуют 12 бегунов. Сколькими способами можно сформировать тройку призеров?

 

·         Игра в бридж.

В игре бридж каждому игроку раздается по 13 карт из колоды карт (52). Сколькими различными способами можно выдать игроку 13 карт?

·         Серия пенальти.

Если финал футбольного чемпионата завершится ничьей, пробивается серия пенальти. Как правило, серия пенальти состоит из 5 ударов, все они выполняются разными игроками. Сколько списков из 5 пенальтистов можно составить из 11 игроков, которые находились на поле?

4. Домашнее задание:

 1) Игрок в бридж при раздаче карт получает 13 карт. Сколькими способами он может упорядочить карты?

2) Выбрать одну азартную игру и составить по ней 2 задачи.

Занятие 12.  Азартные игры. Турнир математиков.

 Аналогично занятию 3,9.

Форма проведения занятия: Интеллектуальная игра

Цели:

·         Развитие познавательного интереса к предмету математика, применение математических знаний во внеурочной обстановке.

·         Развитие у учащихся познавательного интереса и любознательности.

·         Воспитание доброжелательности, инициативности, активности.

Ход занятия:

1. Сообщение темы и цели урока.

2. Задачи, рекомендованные для рассмотрения:

1. Парадокс дней рождения

 (Если дана группа из 23 или более человек, то вероятность того, что, хотя бы у двух из них дни рождения (число и месяц) совпадут, превышает 50%.)

2. Проходит Телеконкурс.

 Одно из заданий телеконкурса состоит в том, что нужно угадать, за какой дверью находится приз. Конкурсанта просят подойти к одной из дверей. Затем, ведущий открывает одну из дверей, не выбранных конкурсантом, за которой нет приза, и предлагает поменять изначально выбранную дверь на другую закрытую. Стоит ли принимать предложение ведущего, чтобы повысить свои шансы на победу?

Раздел 4: «Современные игры»

Занятие 13,14. Разбор современных игр с точки зрения математики.

Форма проведения занятия: определяется учителем.

Изучив предыдущие разделы, ученики понимают, что чем сложнее анализируемые ситуации, и чем они ближе к реальности, тем менее категоричны математические методы, используемые при решении.

Цель: применить полученные навыки перевода игр на математический язык.

В процессе игры вырабатывается привычка сосредоточиваться, мыслить самостоятельно, развивается внимание, стремление к знаниям. Увлекшись, учащиеся не замечают, что учатся: познают, запоминают новое, пополняют запас представлений, развивают фантазию. Данные игры помогают развивать логику, учиться просчитывать ходы на перед, помогает запомнить степени 2. Игры, рекомендованные для рассмотрения:

 

·         Крестики нолики. 

(ученики всегда знают выигрышную стратегию, но необходимо обсудить с ними почему, те или иные последовательности ходов являются выигрышными)

·         2048.

Математическая игра, созданная итальянским разработчиком Gabriele Cirulli. Игровое поле состоит из сетки 4х4. Когда игра начинается на «сцене» две плитки с номиналом 2.Передвигая плитки нужно сложить плитки одного «номинала». Движение возможно в 4 стороны. 

1) Существует ли выигрышная стратегия?

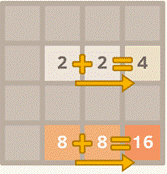
2) Являются ли перечисленные ниже действия выигрышной стратегией?

1.      Создаем «систему» из 4-х плиток. Плитка, с крупным «номиналом» будет «центральной ячейкой», а с меньшими значениями «малыми ячейками».

2.      Расположить ячейки линейно по горизонтали на нижней платформе, при этом исключить движение вверх.

3.      Сумму продвигать справа налево, в «центральную ячейку», через сеть «малых».

·         Drew line.

Draw Line Classi - классическая головоломка. Суть игры состоит в том, чтобы соединить точки по цветам при этом заполнив всю площадь поля. К какому типу игр эта игра относится? В чем ее суть? 

 

·         Карточная игра «Пьяница».

В игре используется колода из 36, 52 или 54 карт. В игре могут участвовать от двух до восьми игроков. Колода раздаётся поровну всем игрокам. Игроки не смотрят в свои карты (как в игре «Дурак»), а кладут их в стопку рядом с собой. Первый ходящий снимает верхнюю карту из своей стопки и кладет её в центр стола в открытом виде. Другие игроки по кругу делают то же самое. Тот игрок, чья карта оказалась старше всех остальных, снимает свою и «битые» карты и кладёт их в другую стопку (вариант: в низ своей стопки); порядок складывания карт в разных вариантах игры может подчиняться тем или иным правилам или быть произвольным, что позволяет вести ту или иную стратегию с целью захватить у соперника как можно более старшие карты. Игрок, потерявший все свои карты, выбывает из игры. Победителем считается игрок, в стопке у которого окажется вся колода. Возможна и игра в поддавки, в которой выигрывает тот, кто раньше остальных избавляется от своих карт.

1)      К какому типу игр относится эта игра?

2)      Существует ли выигрышная стратегия?

В Занятии 14 ученикам дается творческое задание, составить выступление с разбором своей любимой современной игры.

Выступление должно содержать:

-        описание игры;

-        ее математические аспекты;

-        разбор выигрышной стратегии (если такая имеется)

-        составление задач по игре.

Ученики могут предоставить результаты своей работы в виде плаката, газеты, мультимедийного пособия и в других видах.

 

БИБЛИОГРАФИЯ

1.      Алгебра 7-9 класс [Текст] : учебник для общеобразоват. учреждений / Г. В. Дорофеев, Е. А. Бунимович, С. Б. Суворова и др. ; под ред. Г. В. Дорофеева, И. Ф. Шарыгина; Рос. акад. образования. – 5–е изд. – М.: Мнемозина, 2010. – 288 с.

2.      Аникеева, Н. П. Воспитание игрой [Текст] : книга для учителя / Н. П. Аникеева - М.: Просвещение, 1987. – 144 с.

3.      Балк, М. Б. Организация и содержание внеклассных занятий по математике [Текст] / М. Б. Балк - М.: ГУПИ МП РСФСР, 1956. – 248 с.

4.      Болл, У.  Математические эссе и развлечения [Текст] / У. Болл, Г. Коксетер – М.: Мир, 1986. – 470 с.

5.      Болотов, В. А. Письмо Министерства образования Российской Федерации  № 03-93 ин/13-03 о введении элементов комбинаторики, статистики и теории вероятности в содержание математического образования основной школы [Электронный ресурс] – Режим доступа: http://www.math.ru/teacher/doc/9 , свободный.

6.      Большой психологический словарь [Текст] /Б. Г. Мещеряков, В. П. Зинченко. – СПб.: прайм – ЕВРОЗНАК, 2005. – 672 с.

7.      Бунимович, Е. А. Вероятность и статистика 5-9 класс [Текст] / Е. А. Бунимович, В. А. Булычев – М.: Дрофа, 2002. – 160 с.

8.      Выготский, Л. С. Педагогическая психология [Текст] / Л. С. Выготский – М.: АСТ, 2008. – 671 с.

9.      Газман, О. С. Каникулы. Игра, воспитание. О педагогическом руководстве игровой деятельностью школьников [Текст] : книга для учителя / О. С. Газман, З. В. Баянкина и др. – М.: Просвещение, 1988. – 159 с.

10.  Гнеденко, Б. В. Математика в современном мире [Текст] / Б. В. Гнеденко - М.: Просвещение, 1977. – 128 с.

11.  Горев, П. М. Уроки развивающей математики. Задачи математического кружка [Текст] : учеб. пособие для 5-6 кл. / П. М. Горев, В. В. Утемов – Киров: МЦИТО, 2014. – 207 с.

12.  Григорьев, В. М Теория и история игры [Текст] / В. М. Григорьев, С. В. Григорьев. – М.: ОДИ-International, 1995. – 107 с.

13.  Гусева, И. Л. Математика. 6 класс. Тестовые материалы для оценки качества обучения [Текст] : учеб. пособие / И. Л. Гусева – М.: Интеллект-Центр, 2015. – 96 с. 

14.  Дубровский, В. Н. Математические головоломки [Текст] : учеб. пособие / В. Н. Дубровский, А. Т. Калинин – М.: Знание, 1990. – 144 с.

15.  Крутецкий, В. А. Психология обучения и воспитания [Текст] / В. А. Крутецкий – М.: Просвещение, 1976. – 317 с.

16.  Леонтьев, А. Н. Психологические основы дошкольной игры / А. Н. Леонтьев // Советская педагогика. – 1944. – № 8 - 9, с. 37—47.

17.  Математика 6 класс [Текст] : учебник для общеобразоват. учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков. – 25–е изд. – М. : Мнемозина, 2009. – 288 с.

18.  Математика 6 класс [Текст] : учебник для общеобразоват. учреждений / Г. В. Дорофеев, И. Ф. Шарыгин, С. Б. Суворова и др. ; под ред. Г. В. Дорофеева, И. Ф. Шарыгина ; Рос. акад. образования. – 11–е изд. – М.: Просвещение, 2010. – 303 с.

19.  Матюхина, М. В. Возрастная и педагогическая психология [Текст] : учеб. пособие для студентов пед. ин–тов. по спец. № 2121 «Педагогика и методика нач. обучения» / М. В. Матюхина, Т. С. Михальчик, Н. Ф. Прокина и др. ; под ред. М. В. Гамезо и др. – М.: Просвещение, 1984. – 256 с.

20.  Мухина, В. С. Возрастная психология [Текст] : учебник для студентов высших учеб. заведений / В. С. Мухина. – 14-е изд. – М.: «Академия», 2012. – 655 с.

21.  Нестерова, О. В. Педагогическая психология в схемах, таблицах и опорных конспектах [Текст] / О. В. Нестерова – М.: Айрис-пресс, 2006. – 112 с.

22.  Перельман, Я. И. 101 головоломка [Текст] / Я. И. Перельман – М.: АСТ, 2015. – 192 с.

23.  Перельман, Я. И. Весёлые задачи [Текст] / Я. И. Перельман – М.: АСТ, 2014. – 288 с.

24.  Петраков, И. С. Математические кружки в 8-10 классах [Текст] / И. С. Петраков – М.: Просвещение, 1987. – 224 с.

25.  Рыбников, К. А. История математики [Текст] / М.: Издательство Московского Университета, 1963. – 336 с.

26.  Саранцев, Г. И. Методика обучения математике в средней школе [Текст] : учеб. пособие для студентов мат. специальностей пед. вузов и ун-тов, обучающихся по специальности 032100 Математика / Г. И. Саранцев. – М.: Просвещение, 2002. – 223 с.

27.  Фарков, А. В. Внеклассная работа по математике. 5-11 классы. [Текст] / А. В. Фарков – М.: Айрис-пресс, 2008. – 288 с.

28.  Федеральный государственный образовательный стандарт основного общего образования [Текст] / ред. И. А. Сафронова – М.: Просвещение, 2014. – 48 с.

29.  Фридман, Л. М. Психолого-педагогические основы обучения математики в школе [Текст] / Л. М. Фридман – М.: Просвещение, 1983. – 160 с.

30. Heims, S. John Von Neumann and Norbert Wiener: from mathematics to the technologies of life and death [Text] / MIT Press, 1980. — 568 p.

 

31.  Скачано с www.znanio.ru