Разработка урока по геометрии 9 класс по теме «Теорема о площади треугольника»

Разработка урока по геометрии 9 класс по теме «Теорема о площади треугольника.»

Цели:

- доказать теорему о площади треугольника;

- научить учащихся решать задачи на применение теоремы о площади треугольника;

-активизировать познавательную деятельность учащихся, поддержать интерес к предмету;

- воспитывать уважение друг к другу, взаимопонимание, уверенность в себе.

Ход урока.

1. Организационный момент.

1.  Фронтальная работа с классом.

1)  Какие формулы используются для вычисления координат точки А?

(Ответ: х = ОА ∙ cosα; у = ОА ∙ sinα.)

2) Какие формулы используются для вычисления площади:

а) треугольника; б) параллелограмма?

Формулы площади треугольника:

S=ab, где а, b - катеты прямоугольного треугольника,

S= ah, где а - основание треугольника, h- высота,

Формула Герона:

S = , р =  - полупериметр

а, b, с-стороны треугольника

2. Решение задач по готовым чертежам

Найдите площадь треугольника

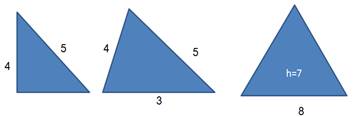
Ответы: 6; 6; 28

3. Изучение нового материала

Вывод формулы о площади треугольника можно получить в процессе решения задачи в творческих группах с последующим обсуждением всех вариантов решений.

Задача:

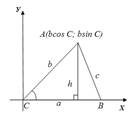
Дано:  Треугольник ABC, BC=a, CA=b, S-площадь треугольника.            

Доказать: S=absinC

Доказательство: S=ah, h=bsinC.

Следовательно: S=absinC

Итак, мы доказали теорему о площади треугольника

Теорема: Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

4. Решение задач на закрепление:

1) № 1020(а)

Дано:      АВС, АВ = 6см, АС = 4 см,  <А = 60˚

Найти: S = ?

Ответ: 12

2) № 1022

Дано: S = 60 см, АС = 15 см, <А = 30˚

Найти: АВ = ?

Ответ: 16 см.

3) Найти площадь равнобедренного треугольника с углом при основании 15˚ и боковой стороной, равной 5 см.

Ответ: см.

4) В параллелограмме АВСD  АВ = 6, АD = 4, sinA = 0,8. Найдите большую высоту параллелограмма.

Ответ: 4,8

5) . Основания равнобедренной трапеции равны 6 и 12. Синус острого угла трапеции равен 0,8. Найдите боковую сторону трапеции

Ответ: 5

5. Самостоятельная работа

6. Домашнее задание:

П. 96, в. 7, № 1020(б, в), № 1021, № 1023

Подведение итогов урока