Разработка урока "Сравнение обыкновенных дробей", 5 класс

Тема. Сравнение обыкновенных дробей.

5 класс

Цели урока:

                                  Обучающая:

·         познакомить с правилом сравнения обыкновенных дробей с одинаковыми знаменателями;

·         сформировать первые навыки записи дробей в порядке возрастания (убывания);

·         закрепить знание взаимного расположения точек на луче в зависимости от их координат.

Развивающая:

·         развивать способность применять знания в новой ситуации;

·         учить формулировать самостоятельно вывод.

Воспитательная:

·         воспитывать скромность и аккуратность.

Ход  урока.

I.Организационный момент.

II.Подготовка к изучению нового материала.

            Какую запись называют обыкновенной дробью?

Запись вида а/в, где а- числитель , а в- знаменатель называют обыкновенной дробью .

         Что показывает знаменатель дроби?

Знаменатель показывает, на сколько долей делят.

         Что показывает числитель дроби?

Числитель показывает, сколько таких долей взято.

         По рисунку 1.

О     С     А             В                             Е

0                                                              1

Рис. 1

         Какая из отмеченных точек имеет координату 1/2, 1/8, 1/4?

В(1/2), С(1/8), А(1/4).

            Сколько  клеток нужно отсчитать от начала отсчета, что бы отметить на рисунке 1 точку М(3/4),  Д(7/8)?

( объяснить).

III.Ознакомление с новым материалом.

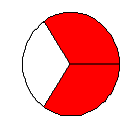
                                                           Запишите, какая часть круга закрашена?  2/3.

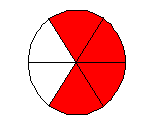
                                                           А сейчас какая часть круга закрашена?  4/6.

Но ведь это одна и та же часть круга! Значит можно сказать, что эти дроби равны?

              Записали 2/3 = 4/6.

Условия, при которых дроби равны, мы будем изучать намного позже, а сейчас важно посмотреть, как будут располагаться точки с равными координатами на луче. Отметьте на координатном луче т А(4/6) и В(2/3), если единичный отрезок равен 12 клеткам.

A (4/6) следовательно =8

B (2/3) следовательно =8

             Выполняют построение в тетради.

О                                                             А                             Е

 0                                                             В                                 1

                                                         Посмотрите, точки на луче совпадают, если дроби равны.

На координатном луче равные дроби соответствуют одной и той же точке.

Далее, вы знаете, что дроби указывают части целого. Как узнать какая дробь больше?

Сравнение обыкновенных дробей.

      Как и натуральные числа, дроби можно сравнивать друг с другом. Проще всего сравнивать дроби с одинаковыми знаменателями.                   

       Правило сравнения таких дробей очевидно из самого понятия дроби. Ясно, что если мы делим какую – то сумму денег на несколько равных частей, то чем больше мы возьмём таких частей, тем больше денег нам достанется. Например, 2/5 < 4/5.

      Легко сравнить и две дроби с одинаковыми числителями. Если мы делим предмет на большее число частей, то каждая часть получается меньше. Например, 1/5 < 1/3. Но тогда  и несколько «маленьких» частей вместе меньше, чем такое же количество «больших» частей: 2/5 < 2/3.

Точка на координатном луче, имеющая меньшую координату, лежит слева от точки, имеющей большую координату.

4. Первичное закрепление

698, 700, 706, 708, 711

Доп. Задание.

Отметьте на координатном луче точки, координаты которых равны:

1/5; 2/5; 3/5;4/5.

О     А     В     С     D     Е

0      1/5   2/5   3/5   4/5   1

Дополнительные вопросы к № 918.

Какая дробь самая маленькая из всех отмеченных?  4/5

Какая дробь самая большая из всех отмеченных?   1/5

Скажите, в каком порядке располагаются дроби на луче? Возрастания или убывания?

Возрастания.

Скажите, какая из дробей будет расположена левее на луче 1/4 или 3/4?  1/4  

Почему?

Потому что 1/4  меньше, чем 3/4.

5. Постановка домашнего задания.

п.23. №-№ 699, 701, 707, 714

   IV.   Итог урока.

Какая дробь из двух дробей с одинаковыми знаменателями меньше, а какая больше?

Как изображаются равные дроби на координатном луче?

Какая из точек лежит на координатном луче левее – с меньшей или с большей координатой?