Реферат

              Министерство образования и науки Российской Федерации

              Муниципальное казенное общеобразовательное учреждение

               «Марковская СОШ» Каменского муниципального района

                                                Воронежской области

 

 

                                           ТАЙНЫ  КРИПТОГРАФИИ

                                                           (реферат)

 

 

 

 

                                                                       Выполнил:

                                                                       учащийся 7 класса

                                                                       МКОУ «Марковская СОШ»

                                                                       Венцель Дмитрий

 

                                                                       Научный руководитель:

                                                                       учитель математики

                                                                       Ромасева Л.В.

 

                                                       с. Марки 2020                                                                     

                                          СОДЕРЖАНИЕ

   Цели и задачи……………………………………………………...      3

I.   Введение………………………………………………………….      4

II.   Основная часть…………………………………………….........      5

    Глава 1. История криптографии...……………………………….      5

    Глава 2. Основы криптографии……………... ………………….      7

    Глава 3. Шифры………………………………..………………....      8

    Глава 4. Шифровальные приборы..……………………………...     10

    Глава 5. Великие математики и криптография………………….    11                 

    Глава 6. Шифрование информации в России.……………….......    13

    Глава 7. Криптография во Второй Мировой войне..……………    14

    Глава 8. Вклад советских математиков криптографов в победу над   

                  Германией………………………………………..……….    15

    Глава 9. Мои исследования……………………………………….    19

III.  Заключение………………………………………………………     20

Список литературы и ресурсы интернета…………………………..     22

Приложение…………………………………………………………..     23

 

 

 

 

 

 

                                          

 Объект исследования: шифры   и их использование.

Предмет исследования: история и основы криптографии; применение шифров великими математиками и вклад криптографов в Победу. 

Проблема: Что такое криптография и её тесное взаимодействие с математикой? Какой вклад внесли криптографы в победу в Великой Отечественной войне?

Актуальность исследования: Необходимость защиты информации и предотвращение возможного вреда от её разглашения. Математический аппарат продолжает оставаться основным в криптографии, поэтому мы должны знать видных математиков, имена которых вписаны в многовековую историю криптографии, факты о вкладе криптографов в Победу над фашистской Германией.

Период исследования: декабрь 2019 –  март 2020г.

Гипотеза исследования: Без тайн не может быть не только государства, но даже малой общности людей - без них нельзя выиграть сражение или выгодно продать товар, одолеть своих политических противников в жесткой борьбе за власть или сохранить первенство в технологии. Тайны составляют основу науки, техники и политики любого человеческого общества.

Цели и задачи исследования. Познакомиться с криптографией; шифрами, их видами и свойствами; показать некоторые связи между математикой и криптографией; познакомиться с математиками, внесшими свой вклад в историю криптографии; определить вклад российских криптографов в победу над фашизмом. Выявить в ходе экспериментов наиболее простые и эффективные способы шифрования. Оформить результаты своих исследований с помощью ИКТ (презентация, буклет).

Методы исследования: изучение литературных источников и источников Интернет; сравнительный анализ полученной информации; отбор информации для работы; анкетирование; эксперимент.

                                    «Рано или поздно всякая правильная математическая идея     

                                            находит применение в том или ином деле».

                                                                                                            А. Н. Крылов

                                                  ВВЕДЕНИЕ

           Все дальше и дальше идут в прошлое года второй мировой войны, но победа в Великой Отечественной войне и победа над фашизмом нашего народа навсегда есть и будет в наших мыслях и сердцах, а также в истории как одно из величайших событий, которое повлияло на мировое развитие. В этом году исполняется 75 лет со дня Победы советского народа в Великой Отечественной войне, немалый вклад в которую внесли наши криптографы. Они не только сумели вскрыть многие шифры нацистской Германии и предоставить руководству ценнейшую разведывательную информацию, но и не позволили противнику получать сведения о наших замыслах и действиях. Разработчики шифров и шифрмашин, шифровальная служба обеспечивали безопасность советских линий связи. Радиоразведчики и дешифровальщики успешно перехватывали и дешифровывали криптограммы фашистской Германии, её европейских союзников, милитаристской Японии.

          Математика и криптография всегда взаимно дополняли и обогащали друг друга. То, что информация имеет ценность, люди осознали очень давно - недаром переписка сильных мира сего издавна была объектом пристального внимания их недругов и друзей, поэтому на протяжении веков руководители государств, политические деятели и высокопоставленные военные активно использовали криптографию.  Тогда-то и возникла задача защиты этой переписки от чрезмерно любопытных глаз, потому что информация может быть настоящим сокровищем. Обычно в таких случаях говорят, что информация содержит тайну или является защищаемой, приватной, конфиденциальной, секретной, введены даже специальные понятия: государственная тайна, военная тайна, коммерческая тайна, юридическая тайна, врачебная тайна и т.д. Нередко успехи и неудачи криптографов оказывали серьезное влияние на ход войн, революций, а также определяли внешнюю и внутреннюю политику государств. Характерным примером служит операция «Ультра», в результате которой английские криптографы во время Второй мировой войны смогли дешифровать переписку в сетях связи вооруженных сил Германии, что послужило   переломом   в ходе боевых действий в Атлантическом океане, Средиземноморье и на Западном фронте в пользу антигитлеровской коалиции.  

       О шифрах я знал только по рассказу Конан Дойля «Пляшущие человечки», а потом, посмотрев фильм «Семнадцать мгновений весны» и познакомившись с шифрами на внеклассном занятии по математике, мне очень захотелось окунуться в удивительный мир криптографии. Захотелось узнать её историю, шифры их виды и свойства, найти связь между математикой и криптографией, узнать о вкладе криптографов в победу над фашизмом и, конечно, попробовать свои силы в одной из наиболее бурно развивающихся областей человеческого знания.

                          ГЛАВА 1. ИСТОРИЯ КРИПТОГРАФИИ

             История криптографии насчитывает около 4 тысяч лет. Криптография - ровесница письменности. Она возникла задолго до Египетских пирамид и к нашему времени, пройдя через этапы «криптография как искусство» и «криптография как ремесло», превратилась в самостоятельную, бурно развивающуюся науку со своими весьма специфическими, но во многом опирающимися на математику методами исследования.  В качестве основного критерия периодизации криптографии возможно использовать технологические характеристики используемых методов шифрования.

Ø Первый период (приблизительно с 3-го тысячелетия до н. э.) характеризуется господством   моноалфавитных шифров (основной принцип — замена алфавита исходного текста другим алфавитом через замену букв другими буквами или символами).

Ø Второй период (хронологические рамки — с IX века на Ближнем Востоке (Ал-Кинди) и с XV века в Европе (Леон Баттиста Альберти) — до начала XX века) ознаменовался введением в обиход полиалфавитных шифров.

Ø Третий период (с начала и до середины XX века) характеризуется внедрением электромеханических устройств в работу шифровальщиков. При этом продолжалось использование полиалфавитных шифров.

Ø Четвертый период — с середины XX до 70-х годов XX века — период перехода к математической криптографии. В работе Шеннона появляются строгие математические определения количества информации, передачи данных, энтропии, функций шифрования. Обязательным этапом создания шифра считается изучение его уязвимости к различным известным атакам — линейному и дифференциальному криптоанализам. Однако до 1975 года криптография оставалась «классической», или же, более корректно, криптографией с секретным ключом.

Ø Современный период развития криптографии (с конца 1970-х годов по настоящее время) отличается зарождением и развитием нового направления — криптография с открытым ключом. Её появление знаменуется не только новыми техническими возможностями, но и сравнительно широким распространением криптографии для использования частными лицами (в предыдущие эпохи использование криптографии было исключительной прерогативой государства). Правовое регулирование использования криптографии частными лицами в разных странах сильно различается — от разрешения до полного запрета.

          Для знакомства с криптографической терминологией очень полезным может оказаться словарь терминов сайта www.cryptofaq.ru. Приведу лишь основные определения.

          Открытый текст — секретное сообщение, как правило, это последовательность двоичных битов.

          Шифртекст — результат зашифрования.

          Зашифрование — процесс преобразования открытого текста в шифрованный с помощью шифра.

          Шифр — семейство обратимых отображений множества последовательностей открытых текстов в множество последовательностей шифртекстов.  Каждое отображение определяется параметром, называемым ключом. Ключ является сменной частью шифра.

          Расшифрование — процесс, обратный зашифрованию, реализуемый при известном значении ключа.

          Дешифрование — процесс получения открытого текста без предварительного знания ключа, взлом.

          Криптография — научная и практическая деятельность, связанная с разработкой криптографических средств защиты информации, а также анализом и обоснованием их криптографической стойкости. В отличие от организационных и других способов защиты информации, под криптографическими понимаются такие, которые используют математические методы преобразования информации;

         Криптоанализ — научная и практическая деятельность по исследованию криптографических алгоритмов с целью получения обоснованных оценок их криптографической стойкости.

                           ГЛАВА 2. ОСНОВЫ КРИПТОГРАФИИ

 

 Одним из разделов математики, который используется в криптографии, является комбинаторика. Она занимается разного рода наборами, которые можно образовывать из элементов некого конечного множества. Элементами комбинаторики являются сочетания, перестановки, размещения

 Для криптографии важным являются такие алгоритмы комбинаторики как правило умножения, выборки и перестановки. На этих алгоритмах основываются способы формирования секретных ключей для симметричных шифров.

Алгоритм - правило умножения.

Если выбор объекта происходит в два этапа и на первом этапе существует n возможностей, а на втором – m возможностей, то итоговое количество вариантов выбора равно n x m. Данное правило используется в 6 классе.

Алгоритм -выборки

Пусть имеется n объектов, и мы выбираем из них m объектов. Это и есть выборки. Количество выборок зависит от следующих факторов:

1) Считаем ли мы различными выборки из одинаковых элементов, но идущих в разном порядке (например, считаем ли мы выборки «abc» и «cab» одинаковыми или различными);

2) Возможно ли выбирать уже выбранный элемент повторно (например, в алфавите «abc», «ccc», «abb» и т.д.);

Алгоритм - перестановки

Часто требуется не выбирать какие-либо элементы, а просто изменять их порядок следования. Для этого применяются перестановки.

 Придумывание хорошего шифра – дело трудоемкое и дорогостоящее. Поэтому желательно увеличить «время жизни» хорошего шифра и использовать его для шифрования как можно большего количества сообщений. Безопасность защищаемой информации определяется в первую очередь ключом, поэтому законные пользователи должны тайно от противника ими обмениваться

  Криптосистемы разделяются на симметричные и ассиметричные. В симметричных криптосистемах и для шифрования, и для дешифрования используется один и тот же ключ. В ассиметричных системах (с открытым ключом) используются два ключа - открытый и закрытый, которые математически связаны друг с другом. Информация шифруется с помощью открытого ключа, который доступен всем желающим, а расшифровывается с помощью закрытого ключа, известного только получателю сообщения.

 

                                              ГЛАВА 3. ШИФРЫ

       Приведу примеры шифров, которые человечество использует с глубокой древности.

      Шифр простой замены характеризуется тем, что при его использовании отдельные части открытого текста заменяются некоторыми эквивалентами.

      Шифр Полибия является оригинальным шифром простой замены. Буквы алфавита в произвольном порядке вписываются в прямоугольник 5х6 (заполнение квадрата и является ключом).

      Шифр Цезаря представлял собой упрощенный вариант шифра простой замены. Чтобы разобрать и прочитать текст, нужно читать всякий раз четвертую букву вместо первой, D вместо А и так далее».

       Шифр Атбаш. Один из первых шифров. Порой священные иудейские тексты шифровались методом замены, когда вместо первой буквы алфавита писалась последняя буква, вместо второй – предпоследняя и так далее.

       Шифр вертикальной перестановки. Шифром перестановки называется некоторая вполне определенная перестановка элементов открытого текста. За элементы перестановки принимаются отдельные буквы текста. Ключом в данном шифре является порядок перестановки букв.

       Шифр «Штакетник»; Шифр «Змейка»

       Шифр Ришелье.  Кардинал Ришелье (1585-1642) фактический правитель Франции уделял большое внимание как защите информации с помощью шифров, так и вопросами дешифрования. Это оригинальный шифр перестановки с переменным ключом.

       Магический квадрат. Магическими квадратами называют квадратные таблицы с вписанными в их клетки последовательными натуральными числами, начиная от 1, которые дают в сумме по каждому столбцу, каждой строке и каждой диагонали одно и то же число.

        «Решетка Кардано». Из плотного материала вырезался прямоугольник произвольных размеров, например, 7'10 клеток. В прямоугольнике проделывались окна. Секретный текст вписывался в эти окна, затем решетка снималась и оставшиеся клетки заполнялись так, чтобы получалось сообщение, не вызывающее подозрений.

 

                                    ГЛАВА 4. ШИФРОВАЛЬНЫЕ ПРИБОРЫ.

 

      Первый шифровальный прибор – сциталу (скитала) создали в Спарте примерно в V–VI веках до нашей эры.  Он представлял собой два цилиндра одинакового диаметра.

      «Диск Энея». Эней Тактик в IV веке до н.э. предложил устройство, названное впоследствии "диском Энея". Принцип его был прост. На диске диаметром 10-15 см и толщиной 1-2 см высверливались отверстия по числу букв алфавита. В центре диска помещалась "катушка" с намотанной на ней ниткой достаточной длины. При зашифровании нитка "вытягивалась" с катушки и последовательно протягивалась через отверстия, в соответствии с буквами шифруемого текста. Диск и являлся посланием.    

     «Диск Альберти» - устройство, реализующее шифр многоалфавитной замены, изобрел Леон Баттиста Альберти (1404-1472) итальянский ученый, архитектор. «Диск Альберти» состоял из двух дисков – внешнего неподвижного (на нем были нанесены буквы в алфавитном порядке и цифры 1,2,3,4) и подвижноговнутреннего диска на котором буквы были переставлены. Процесс шифрования заключался в нахождении буквы открытого текста на внешнем диске и замене ее на букву с внутреннего диска, стоящую под ней. После этого внутренний диск сдвигался на одну позицию и шифрование второй буквы производилось уже по-новому шифралфавиту. «Диск Альберти» является одним из первых механических устройств шифрования. В области криптографии его заслугой стал так же «Трактат о шифрах».

       Шифровальной техникой времен Второй мировой войны считают знаменитую немецкую шифровальную машину «Энигма» (загадка) — изобретение инженера Артура Шербиуса 1918 года. Этим дисковым шифратором с 1926 года стали оснащаться вооружнные силы и спецслужбы Германии. По некоторым оценкам для вооружения немецкой армии было выпущено до 100 000 её экземпляров.

       В 30-е годы образцы советской шифровальной техники создавались под руководством талантливого инженера Ивана Павловича Волоска. Шифрмашины того времени реализовывали наложение случайной последовательности (гаммы) на открытое текстовое сообщение. В-4, М-100 — одни из первых советских шифрмашин, реализующих шифры гаммирования. М-100 состояла из трех основных узлов: клавиатуры с контактными группами, лентопротяжного механизма с трансмиттером и приспособления, устанавливаемого на клавиатуру пишущей машинки, и семи дополнительных блоков. Общий вес комплекта достигал 141 кг. Только одни аккумуляторы для автономного питания машины весили 32 кг. В 1938 году началось их серийное производство. К первому периоду войны относится разработка портативной, исполненной в виде чемодана, засекречивающей аппаратуры СИ- («Синица») и САУ-16 («Снегирь»), которая использовалась в основном при выездах высшего командного состава в пункты, не имевшие ВЧ-станций.

         Позднее появились и более компактные машины. Например, К-37 («Кристалл»), М-101 («Изумруд»), «Агат», М-125 «Фиалка» и другие. Широко использовалось и ручное шифрование. Телеграммы отправлялись с помощью легких, весом в 3 кг, радиостанций «Север».

  ГЛАВА 5. ВЕЛИКИЕ МАТЕМАТИКИ И КРИПТОГРАФИЯ.

     Криптография всегда развивались в тесном взаимодействии с математикой. Математический аппарат продолжает оставаться основным в криптографии. Ведь не случайно в многовековую историю криптографии вписано много имен видных математиков.

     Одним из первых дешифровальщиков древности был знаменитый греческий философ Аристотель (384-322 до н.э.) автор способа дешифрования сциталы. Он предложил использовать для этого конусообразное «копье», на которое наматывался перехваченный ремень, который передвигался по оси до того положения, пока не появлялся осмысленный текст.

     Применял шифрование и другой великий математик древности – Пифагор. Знаменитый греческий философ Платон отмечает, что "с великим трудом и большой ценой добыл один из манускриптов Пифагора, который никогда не записывал свое эзотерическое учение иначе, как тайными знаками и под различными символами". Впоследствии Платон передал шифрованный текст Пифагора Аристотелю.

          Джероламо Кардано (1501-1576) итальянский математик, философ, врач и изобретатель. Издал ряд трудов по алгебре, а также является автором первой в мире книги по теории вероятности. В криптографии известен изобретением оригинального шифра, называемого «решеткой Кардано».

      Франсуа Виет (1540-1603) французский математик, «отец алгебры». В криптографии известен успешной дешифровальной работой при дворе французских королей Генриха III и Генриха IV, он сумел расшифровать код перехваченной переписки короля Испании с его представителями в Нидерландах. Код был сложным, содержал до 600 различных знаков, которые периодически менялись. Будучи чем-то увлечен, ученый мог работать по трое суток без сна.                      

          Исаак Ньютон (1643-1727). Знаменитый английский ученый в молодости интересовался криптографией и разработал ряд собственных шифров, в последующие годы занялся «дешифрованием» Библии.

          Почетные члены Санкт-Петербургской академии наук (АН) ученые-  математики Леонард Эйлер (1707-1783) и Карл Фридрих Гаусс (1777-1855) активно интересовались криптографией, а Эйлер даже принимал участие в разработке российских государственных шифров и занимался дешифровальной работой. Их достижения в области теории чисел вместе с результатами знаменитого французского математика Пьера Ферма (1601-1665) во второй половине ХХ века были использованы при разработке принципов нового направления в криптографии – систем шифрования с открытым ключом.

             Фурье Жан Батист Жозеф (1768-1837) французский математик и физик, почетный член Санкт-Петербургской АН. Со второй половины ХХ века по настоящее время преобразование Фурье широко используется при создании аппаратуры засекречивания речевого сигнала, а также для криптоанализа подобных систем.

                       ГЛАВА 6. ШИФРОВАНИЕ ИНФОРМАЦИИ В РОССИИ.

      В России шифрование информации использовалось с момента становления государства. Первые профессиональные криптографы   появились при Иване Грозном (1530–1584). Криптографы разрабатывали так называемые «азбуки», «цифири», «цифры» или шифры, как они стали называться позднее. Особое значение криптография приобрела при императоре Петре I. Именно он поставил шифровальную службу действительно на профессиональную основу. Авторство некоторых цифирей принадлежало лично Петру I.

      Дешифровальная служба России достигла больших успехов во время правления императриц Елизаветы Петровны и Екатерины II. Её возглавлял один из первых академиков Санкт-Петербургской АН математик, работавший в области математического анализа и теории чисел Христиан Гольдбах (1690-1764). Криптографическая служба России в то время находилась на достаточно высоком профессиональном уровне. Очень быстро и эффективно работали «чёрные кабинеты» -  тайные комнаты, имевшихся во всех крупных почтовых отделениях в которых вскрывались письма.

          Павел Львович Шиллинг — крупнейший криптограф XIX века, с 1803 года работал в МИД. Именно он организовал министерскую литографию — способ плоской печати, только что входивший в употребление в Европе. До этого шифрдокументы копировались от руки. Ему принадлежит изобретение биграммного шифра, в котором шифровались не отдельные буквы, а их двойные сочетания, биграммы.

     Важную роль сыграли наши дешифровальщики в достижении победы над Наполеоном, в Первой мировой войне, во время военных конфликтов 1920-х-1930-х годов (Испания, Китай, Халхин-Гол и др.).   Эта информация позволяла изменять ход военных действий в нашу пользу. Большое влияние на развитие криптографии в XIX веке оказало изобретение телеграфа, телефона, радио, т. к. резко увеличилась скорость передачи информации. В 1921 году был создан Спецотдел, который стал заниматься как разработкой шифров для правительства, дипломатов и армии, так дешифрованием сообщений противников СССР.  Возглавил новую криптографическую службу с1921 года Глеб Иванович Бокий (1879– 1937). В 1924 году на основе 52 различных шифров был создан так называемый «русский код», дешифровать который не удалось никому.

ГЛАВА 7. КРИПТОГРАФИЯ ВО ВТОРОЙ МИРОВОЙ ВОЙНЕ.

           Наши криптографы накануне Великой Отечественной войны предупредили руководство страны о нападении Германии.  Они построили математическую теорию таких шифров, что дало возможность еще в ходе войны создать отечественные машины и обосновать невозможность их дешифрования с помощью сверхмощной, для того времени, вычислительной техники. Криптографы предоставили политическому и военному руководству СССР большое количество важнейшей информации. Радиодивизионы особого назначения (ОСНАЗ) вели перехват открытых и шифрованных сообщений немцев и их союзников в прифронтовой полосе. Занимались пеленгацией вражеских передатчиков, создавали радиопомехи. Участвовали в операциях по дезинформации противника, совместно с другими видами разведки удалось вскрыть создание немцами ударных группировок для наступления на Москву в самые драматические дни октября 1941 года.  В то же время шифровальная служба не позволила противнику получить сведения о наших замыслах и действиях. Эта информация поступала во время всех важнейших сражений (в т.ч.  Сталинградской битвы, сражения на Курской дуге и т.д.) и способствовала нашим победам. Вот как оценивает работу советских шифровальщиков прославленный полководец Великой Отечественной. Г.К. Жуков: «Хорошая работа шифровальщиков помогла выиграть не одно сражение»

       Многое дают понять эти слова А. Гитлера.   «Эти проклятые русские шифровальные машины, мы никак не можем их расколоть!»  Однако немцам так и не удалось дешифровать сообщения, зашифрованные с помощью советской техники, а с 1942 года эти сообщения перестали перехватывать.   За период войны было обработано свыше 1,6 миллионов шифротелеграмм. Офицеры спецсвязи на грани жизни и смерти, часто с тяжелейшими ранениями, уничтожали шифровальные документы перед приходом врага. Советские шифровальщики под страшными пытками не выдавали ни наших кодовых таблиц, ни особенностей использования нашей шифровальной техники.

ГЛАВА 8. ВКЛАД СОВЕТСКИХ МАТЕМАТИКОВ КРИПТОГРАФОВ В ПОБЕДУ НАД ГЕРМАНИЕЙ.                               

            А какой же вклад внесли в победу над фашистской Германией математики криптографы? Об этом я и хочу вам рассказать.

            Андрей Андреевич Марков (1903-1979) - член-корреспондент АН СССР, математик, занимался проблемами математической логики, алгоритмической сложности и др. До сих пор остается актуальной его теорема о шифрах не размножающих искажений, а теория марковских цепочек для шифрования оказалась в дальнейшем невероятно продуктивной.

           Михаил Спиридонович Одноробов (1910-1997) – подполковник, криптографом военной мобилизации с 1941 года. Внес заметный вклад в совершенствование криптографии и подготовку кадров для нее.  Еще в апреле-мае 1941 г. его и около полусотни молодых ученых из МГУ — математиков и (меньше) физиков, мобилизуют в советскую криптографическую службу. Они не только смогли быстро найти в ней свое место, но и привнесли в криптоаналитическую работу новые идеи, анализируя логику построения лишь частично известного ключа, находили алгоритмы его существенного пополнения, создавали и внедряли в анализ шифров вспомогательную технику.  Эти факторы способствовали совершению качественного скачка в раскрытии часто изменяющихся ключей вермахта. После войны М. С. Одноробов неоднократно выполнял поручения Правительства по оказанию помощи дружественным странам в организации шифрованной связи. Награжден 4 орденами (Красного Знамени, Отечественной войны и Красной Звезды дважды) и 25 медалями.

          Георгий Иванович Пондопуло (1910-1996) полковник, кандидат физико-математических наук, профессор, заслуженный деятель науки РСФСР. Одаренный криптограф. Им лично и под его руководством было раскрыто много сложных шифров иностранных государств. Созданная им методика раскрытия ряда систем ручного шифрования имела большое практическое значение. Активно участвовал в обучении криптографов - начальник кафедры криптографии (впоследствии спецкафедра-7) Высшей школы КГБ СССР. Награжден орденом «Знак Почета» и многими медалями.

          Михаил Иванович Соколов (1914-1999) - кандидат физико-математических наук, полковник, доцент, старший научный сотрудник. С 1941 года работает в Специальной службе Генерального штаба Красной Армии, а затем в Специальной службе органов госбезопасности. Внес большой вклад в дешифрование переписки Германии и ее союзников во время Великой Отечественной войны. После войны работал в криптографических подразделениях и участвовал в обучении молодых криптографов, преподавая им новые математические методы анализа шифров и дешифрования шифрпереписки.  Им написан оригинальный учебник по криптографии, в котором обобщен опыт практической работы по различным видам, так называемых, ручных шифров. Эта книга до сих пор является обязательным пособием при подготовке криптографов - математиков любого уровня.  Автор многих научных работ и учебника по криптографии.  Награжден 2 орденами и 20 медалями.

            Андрей Николаевич Колмогоров (1903-1987) - академик АН СССР, внес существенный вклад во многие разделы математики. Особое значение для приложения математических методов к естествознанию и практическим наукам имел закон больших чисел. В криптографии нашли применение его работы по теории информации и теории вероятностей, в частности, его критерии случайности последовательностей, а также метод “отгадывания” по исследованию среднего количество информации, передаваемой буквой открытого текста. А.Н. Колмогоров не оставлял преподавания в средней школе в течение всей своей жизни. Он - создатель учебников по математике. Академик Колмогоров - почетный член многих иностранных академий и научных обществ, удостоен "Нобелевской премией математиков", Герой Социалистического Труда.                

           Владимир Александрович Котельников (1908-2005) академик АН СССР опубликовал фундаментальные труды в области радиотехники, теории помехоустойчивой связи, радиолокации. Под его руководством в 1930 годы были созданы первые отечественные аппараты для шифрования речевого сигнала.  В 1941 году Владимир Александрович доказал, что можно создать математически недешифруемую систему засекречивания, если каждый знак сообщения будет засекречиваться выбираемым случайно и равновероятно знаком гаммы, математически формализовал требования к стойкости шифров. Подобные системы он стал называть совершенно секретными шифрами, доказал теорему отсчетов (другое название — теорема дискретизации) в которой говорится о возможности восстановления непрерывных функций с ограниченным спектром по их значениям через определенные интервалы времени.  Под руководством Котельникова была разработана сложная засекречивающая аппаратура С-1 («Соболь»), в которой, для хорошей маскировки речевого сигнала, использовались частотные преобразования и временные перестановки отрезков речи одновременно и, которая стала широко использоваться в действующей армии. Уже к осени 1942 года сотрудники лаборатории Котельникова изготовили несколько образцов оборудования «Соболь-П», который использовался для обеспечения секретной связи самого высокого уровня, причем впервые такая связь осуществлялась с помощью радиоканала. Достигнутые им криптографические успехи без преувеличения внесли огромный вклад в нашу победу, а сам В. А. Котельников снискал себе негласный титул «патриарха секретной телефонии». Как вспоминали ветераны ВОВ, применение шифраторов Котельникова в ходе решающих боев на Курской дуге в значительной степени определило успешный исход битвы.  По сведениям советской разведки, А. Гитлер заявлял, что за одного криптоаналитика, способного «взломать» советскую радиосвязь, он не пожалел бы трех отборных дивизий. Результаты своих исследований В. А. Котельников представил в секретной научной работе «Основные положения автоматической шифровки» (1941). С этого времени и началась криптография как наука.  С 1954 года В. А. Котельников возглавил недавно созданный Институт радиотехники и электроники (ИРЭ), в 90-е годы был одним из шести основателей Академии Криптографии. В. А. Котельников — лауреат Ленинской премии, дважды лауреат Государственной премии СССР, дважды Герой Социалистического труда. Он награжден шестью орденами Ленина, орденом «За заслуги перед Отечеством» I степени, другими орденами и медалями, в частности орденом «За заслуги перед Москвой». Ему были присуждены высшие международные награды — премия Э. Рейна и Золотая медаль А. Белла. Решением Международного астрономического союза астероид №2726 носит имя «Kotelnikov». Президент Международного Института электронной и электрической инженерии Брюс Эйзенштейн (США) признавал самый существенный вклад Котельникова в развитие радиосвязи и криптографии.

              Владимир Яковлевич Козлов (1914 - 2007) крупный советский и российский математик, генерал-майор, член-корреспондент Академии наук СССР (РАН), действительный член Академии криптографии РФ, занимался разработкой аппаратуры и теоретическими исследованиями. Это: теоретическая и прикладная криптография, методы кодирования в криптографии, разработка и исследование свойств шифраппаратуры, технологии автоматического распознавания речевых образов, компрессия речевых сигналов, обучаемые и самообучающиеся, алгоритмы распознавания сигналов, а также другие самые современные разделы математики, которые активно внедрялись в отечественную криптографию и формировали новые математические по своей основе разделы криптографии. В.Я. Козлов не только формулировал и ставил стратегические задачи, определял основные направления развития криптографии, но также создал соответствующую научную школу. Значительной вехой является выработка научных критериев оценки качества – стойкости шифров, совершённая по его инициативе. Так же, благодаря ему, в 1989 году в стране появился новый академический журнал «Дискретная математика», в котором статьи по различным направлениям дискретной математики и решает математические проблемы криптографии и защиты информации. Он принимал участие в разработке российского стандарта шифрования. Среди криптографов-математиков В.Я. Козлов – первый, кому было присвоено генеральское звание, и кто был избран в 1966 году членом-корреспондентом Академии наук СССР. Он награждён 5 орденами – орденом Ленина, орденом Октябрьской Революции, двумя орденами Трудового Красного Знамени, орденом Знак Почёта и многими медалями, удостоен звания лауреата Государственной премии СССР в 1986 году. Научно-инженерная школа, выстроенная талантливым «математиком в погонах» Владимиром Яковлевичем Козловым, продолжает служить отечественной криптографии.

                    Не будем забывать про их успехи. Подвиг их бессмертен!

 ГЛАВА 9. МОИ ИССЛЕДОВАНИЯ.

          Познакомившись с различными способами шифрования текстов, я провел небольшое исследование. В исследовании приняли участие 19 учеников 6-8 классов и вот какие результаты у меня получились. (Приложение).

          Вывод: Большинство учащихся о криптографии ничего не знают, хотя понятие шифр им знакомо и им бы хотелось узнать побольше о способах шифрования информации и, конечно, научиться шифровать самим.

          Изучив некоторые шифры, я предпринял попытку закодировать какое-либо сообщение самостоятельно и вот что у меня получилось! (Презентация)

          Вывод: Заниматься шифрованием очень интересно и полезно. Способы шифрования очень разнообразны и оригинальны и, не зная ключа, расшифровать информацию не просто, требуется выдержка, усидчивость и, конечно, математический склад ума.

ЗАКЛЮЧЕНИЕ

         Криптография – одна из самых интересных и актуальных тем. Ведь на протяжении всей истории человечества информация пользовалась большим спросом, поэтому всегда были необходимы люди, умеющие ее защищать и скрывать от посторонних. А решает проблемы защиты информации криптография, наука с древней историей и большими перспективами. Интересно, что основными методами исследования в криптографии являются математические, поэтому криптография широко использует такие разделы математики, как комбинаторика и теория чисел. А значит, только люди, владеющие математикой, могут освоить эту интересную науку, понять её основные законы и принципы, внести свой вклад в её дальнейшее развитие.

        Занимаясь изучением этой темы, я узнал много нового о шифрах и их видах, о вкладе великих математиков в развитие криптографии на войне советских математиков – криптографов. Ценная информация, добытая героями невидимого криптографического фронта, позволила сохранить жизни тысяч и тысяч наших солдат и офицеров, сыграла значительную роль в победе над врагом.                                       

          В настоящее время криптография как наука развивается высокими темпами и современные методы ее защиты напрямую связаны с программированием и созданием различных электронных кодов и шифров. Я, как человек, увлекающийся математикой, планирую связать свою жизнь с деятельностью, использующей математические методы и модели, хотела бы продолжать изучение математических основ защиты информации и, быть может, когда-нибудь в будущем внести свой вклад в совершенствование методов криптографии и разработку новых шифровальных систем.

          В эпоху развития информационных и телекоммуникационных технологий очень важно, чтобы каждый образованный молодой человек имел не только знания в этой области, но и ощущал меру ответственности за владение ими. Существует очень точная поговорка, свидетельствующая о важности этой науки в мире: " Кто владеет информацией, тот владеет миром". 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

СПИСОК ЛИТЕРАТУРЫ

1.     Энциклопедический словарь юного математика для среднего и старшего школьного возраста. М.: Педагогика,1989.

2.      Виленкин Н.Я. Математика и шифры. «Квант» для младших школьников.

3.     Ященко В. В. Основные понятия криптографии // Математическое просвещение. Сер. 3. №2. 1998. С. 53-70.

4.     Б. А. Погорелов. Мы учим хранить и разгадывать тайны. "Красная звезда", 1993, 29 июля, № 170 (21157). 

5.     Алферов А.П., Зубов А.Ю., Кузьмин А.С., Черемушкин А.В. Основы криптографии. Учебное пособие. М., Гелиос АРВ, 2005.

6.      Андреев Н.Н. “Россия остается в числе лидеров мировой криптографии”. Защита информации. Конфидент, 1998, №5, с.12-17.

7.      Астрахан В.И., Павлов В.В., Чернега В.Г., Чернявский Б.Г. Правительственная электросвязь в истории России. Часть I (1917-1945). М., Наука, 2001.

8.      Гольев Ю.И., Ларин Д.А., Тришин А.Е., Шанкин Г.П. Криптография: страницы истории тайных операций. М.: Гелиос АРВ, 2008.

9.     Соч.: А.В.Австриаков, В.И.Гущин, А.П.Тимошенков Шифры замены
ИКСИ: 15

10.  Соч.: М.И.Соколов Шифры перестановки и перестановки; М.И.Соколов Учебник криптографии: Часть 1-я. Курс раскрытия шифров замены, гаммирования и перестановок, М., 1954

Ресурсы интернета:

1.  http://www.agentura.ru

2.  www.cryptography.ru

3.  www.cryptolimp.ru

4.   http://en.wikipedia.org

 

                                                 ПРИЛОЖЕНИЕ

I. Мои исследования

№	Вопрос	Количество ответов «ДА»	Количество ответов «НЕТ»
1	Знаете ли вы, что такое шифр?	17       (89,4%)	2        (10,6%)
2	Знаете ли вы, что такое криптография?	3        (16%)	16       (84%)
3	Пробовали ли вы когда-нибудь зашифровать текст?	13       (68%)	6         (32%)
4	Хотелось ли узнать о разных видах шифрования и хотели бы вы научиться шифровать информацию?	17      (89,4%)	2        (10,6%)

 

 

 

 

 

 

 

 

 

 

 

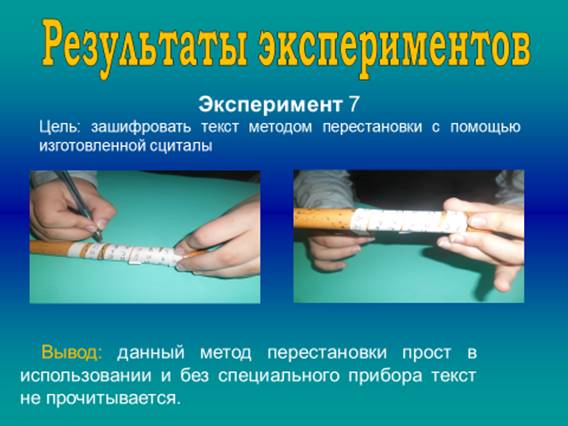
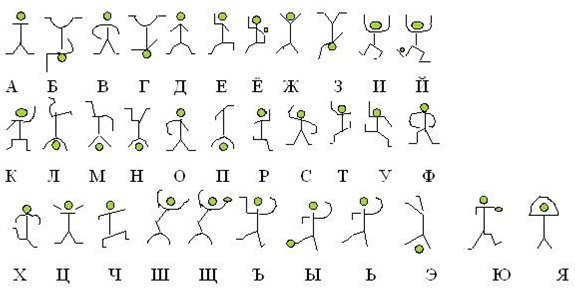
II. Виды шифров

1. «Пляшущие человечки»

    В одном из лучших рассказов английского писателя Артура Конан Дойля великий сыщик Шерлок Холмс расшифровал таинственные записки, которые состояли из изображений пляшущих человечков.  Оказалось, что каждый человечек обозначал одну букву алфавита. Несколько человечков в ряд составляли слово. Так получался непонятный посторонним текст.

Пляшущие человечки оказались шифром простой замены с флагами — разделителями слов. Шерлок Холмс, проанализировавший ранее 160 различных шифров, взломал шифр методом атаки на основе подобранного открытого текста.

2. Шифр простой замены.

     Шифр простой замены характеризуется тем, что при его использовании отдельные части открытого текста заменяются некоторыми эквивалентами. Для построения шифра простой замены необходимо выписать буквы алфавита (в алфавитном порядке) и под ними подписываются произвольно переставленные буквы этого алфавита, группы цифр или различные символы, например:

АБВГДЕЖЗИКЛМНОПРСТУФХЦЧШЩЫЬЭЮЯ

ПЕЦЧЖРЭАНВОЗТБСИУФГХЛЩДЯЬЮКШЫМ 

     Данная подстановка однозначно задает соответствие между знаками открытого и шифрованого текста и является ключом.

Зашифруем слово «криптография» по первому ключу, получим следующий шифртекст:

ВИНСФБЧИПХНМ.

    3. Шифр Полибия

      Шифр Полибия является оригинальным шифром простой замены. Приведем пример этого шифра для русского языка. Буквы алфавита в произвольном порядке вписываются в прямоугольник 5х6 (заполнение квадрата и является ключом) например, так:

     Шифр- текст представляет собой координаты буквы открытого текста (номер строки и номер столбца или наоборот). При шифровании слова «победа» по данному ключу получим следующий шифр-текст: 55251335 312 3.

     Полибий в своей девятой книге «Всеобщая история» указал способ передачи сведений на расстояние при помощи световой факельной сигнализации из 10 факелов.     Шифр Полибия применяли декабристы, когда после восстания 1825 года некоторые из них находились в заключении в Петропавловской крепости. Этот шифр нередко называли «тюремным шифром».

4. Шифр Цезаря

     Шифр Цезаря представлял собой упрощенный вариант шифра простой замены. Чтобы разобрать и прочитать текст, нужно читать всякий раз четвертую букву вместо первой, D вместо А и так далее». Таким образом, нижняя строка замены образовывалась циклическим сдвигом алфавита открытого текста на 3 буквы влево:

ABCDEFGHIJKLMNOPQRSTUVWXYZ

DEFGHIJKLMNOPQRSTUVWXYZABC

5. Шифр Атбаш.

      Один из первых шифров. Порой священные иудейские тексты шифровались методом замены, когда вместо первой буквы алфавита писалась последняя буква, вместо второй – предпоследняя и так далее.

6. Шифр вертикальной перестановки

     Шифром перестановки называется некоторая вполне определенная перестановка элементов открытого текста. За элементы перестановки принимаются отдельные буквы текста. Ключом в данном шифре является порядок перестановки букв. Шифр вертикальной перестановки является одним из частных случаев шифра перестановки. Суть его заключается в следующем. Возьмем некий ключ, например 3 6 7 9 4 1 8 2 10 5, и пусть имеется открытый текст:

 

Осуществляя по ключу перестановку столбцов получаем шифртекст:

     Выпишем текст по столбцам в одну строку:

ЖЬЮИАСЗФОАННАОМВООИМЩРПКНИСФЛТМИЦЮИРЩРОЕИВОТИШКЕТАЬТЕИОНПРЬА

В случае если длина текста меньше размера таблицы, то свободные ячейки заполняются произвольными буквами. Шифр горизонтальной перестановки отличается тем, что выписка шифр- текста производится по строкам.

7. Шифр «Штакетник»

     В начале для удобства шифрования текст записывают без пробелов и знаков препинания (для удобства шифрования и дешифрования), затем текст разбивают на две части одинаковой длинны, если число букв нечетное добавляют случайную букву. Записывают в две строчки – одну выше, а вторую ниже примерно так:

М

т

м

т

к

ц

р

ц

н

у

а

е

а

и

а

а

и

а

а

к

Затем переписывают верхний ряд, а затем нижний, так чтобы нижний был продолжением верхнего. Надпись должна быть написана в одну строчку.

мтмткцрцнуаеаиааиаак

8. Шифр «Змейка»

   Есть еще другой способ шифрования перестановкой букв.

   Берется текст предназначенный для шифрования. Текст записывается без пробелов:

секретныйагентнольнольсемь.

   Текст разбивается на группы по 5 букв, а последнюю букву «ь» отбрасываем и получаем.

секре тныйа гентн ольно льсем

   Затем вписываем в таблицу 5 Х 5. В каждом квадрате по одной букве. Первую букву располагаем в верхнем левом квадрате, а заполняется слева на право сверху вниз. Получится следующая таблица:

С	Е	К	Р	Е
Т	Н	Ы	Й	А
Г	Е	Н	Т	Н
О	Л	Ь	Н	О
Л	Ь	С	Е	М

    Затем перепишите буквы по направлению отсчета с 1 по 25 клетку. А начните с нижней левой клетки.

5	6	15	16	25
4	7	14	17	24
3	8	13	18	23
2	9	12	19	22
1	10	11	20	21

В результате получается следующее сообщение:

ЛОГТС ЕНЕЛЬ СЬНЫК РЙТНЕ ЕАНОМ

    Если послать это сообщение своему знакомому, а он будет знать особенности этого шифра, то он сможет прочитать ваше сообщение

    Можно понять, что используя этот принцип шифрования можно достаточно надежно скрыть свое сообщение, так как порядок шифрования зависит исключительно от вашей договоренности с другом.

9. Шифр Ришелье

    Кардинал Ришелье (1585-1642) фактический правитель Франции уделял большое внимание как защите информации с помощью шифров, так и вопросами дешифрования. Ришелье изобрел оригинальный шифр, который до сих пор носит его имя. Это оригинальный шифр перестановки с переменным ключом. Его использование становится понятным из следующего примера:

 

         Ключ: 2741635; 15243; 671852493; 07;28615;943;...

         Открытый текст:

         LETTER SENT TO THE EMPEROR GIVING FULL DETAIL

         Ключ:

         (2741635) (15243) (671852493) (07) (28615)(943)(2741635)

         Шифртекст:

         TLRTSEE ETOTN EPOEMTHER NI LUGIG VFR TLIE SAD

 

     Известно, что Ришелье пользовался также кодами.

10. Магический квадрат

Магическими квадратами называют квадратные таблицы с вписанными в их клетки последовательными натуральными числами, начиная от 1, которые дают в сумме по каждому столбцу, каждой строке и каждой диагонали одно и то же число.

Шифруемый текст вписывали в магические квадраты в соответствии с нумерацией их клеток. Если затем выписать содержимое такой таблицы по строкам, то получится шифртекст, сформированный благодаря перестановке букв исходного сообщения. В те времена считалось, что созданные с помощью магических квадратов шифртексты охраняет не только ключ, но и магическая сила.

Пример магического квадрата и его заполнения сообщением СПАСИБО ЗА ПОБЕДУ  показан на рис.

16	3	2	13
5	10	11	8
9	6	7	12
4	15	14	1

О	А	П	Е
И	П	О	З
А	Б	О	Б
С	У	Д	С

 

Шифртекст, получаемый при считывании содержимого правой таблицы по строкам, имеет вполне загадочный вид:

ОАПЕ ИПОЗ АБОБ СУДС

Число магических квадратов быстро возрастает с увеличением размера квадрата. «Существует только один магический квадрат размером 3х3 (если не учитывать его повороты). Количество магических квадратов 4х4 составляет уже 880, а количество магических квадратов 5х5 - около 250000»

11. «Решетка Кардано».

     Джероламо Кардано (1501-1576) итальянский математик, философ, врач и изобретатель. Издал ряд трудов по алгебре, а также является автором первой в мире книги по теории вероятности. В криптографии известен изобретением оригинального шифра, называемого «решеткой Кардано». Из плотного материала вырезался прямоугольник произвольных размеров, например, 7´10 клеток. В прямоугольнике проделывались окна. Секретный текст вписывался в эти окна, затем решетка снималась и оставшиеся клетки заполнялись так, чтобы получалось сообщение, не вызывающее подозрений.

     Этот шифр использовался во многих странах в разные времена, в том числе и во время Второй мировой войны.

12. Широкое распространение получили так называемые акростихи, изобретенные еще в V веке до н.э., в которых «секретное» послание скрывается за начальными буквами строк.

Приближается славная дата,

Отчего же так сердце болит?

Будто деды сражались напрасно,

Если где-то орудье гремит.

До чего же нам хочется мира,

А война нам совсем не нужна.

В этом стихотворении зашифровано слово «ПОБЕДА»

 

 

 

 

 

 

 

Скачано с www.znanio.ru