Реферат. Моделирование при решении текстовых задач в начальной школе

Государственное бюджетное образовательное учреждение

среднего профессионального образован я

«Педагогический колледж им. Н. К. Калугина»

г. Оренбурга

Специальность 44.02.02

 «Преподавание в начальных классах»

Реферат

на тему: " Моделирование при решении текстовых задач в начальной школе "

Выполнила: Асатрян Диана Армановна

студентка 28А группы,

Руководитель: Александрова Н.А.

Оренбург

2021 год

Содержание

Введение.......................................................................................................... 3

1.Моделирование и его виды........................................................................... 4

2. Понятие модели и ее построение................................................................. 6

3.Текстовые задачи и процесс их решения...................................................... 7

4.Моделирование в процессе решения текстовых задач.................................. 9

Заключение.................................................................................................... 13

Список использованной литературы.............................................................. 14

Введение

Решению текстовых задач отводится достаточно много времени в школьном курсе математики. В ходе работы над задачами педагог раскрывает связи между данными и искомыми величинами, отношения, заданные в условии.

Учебная деятельность при решении задач складывается из умственных действий и осуществляется эффективно, если первоначально она происходит на основе внешних действий с предметами. Главной проблемой остается то, что дети не могут перейти от текста задачи к математической модели.

Обучение математике требует развития у детей самостоятельности в решении текстовых задач. Каждый ученик должен уметь кратко записывать условие задачи, иллюстрируя ее с помощью рисунка, схемы, чертежа и других видов моделей.

 «Рисунки, схемы, чертежи не только помогают учащимся в сознательном выявлении скрытых зависимостей между величинами, но и побуждают активно мыслить, искать наиболее рациональные пути решения задач. Эти условия необходимы для того, чтобы обучение носило развивающий характер»

Главное для каждого ученика на этом этапе – понять задачу, уяснить, что в ней известно, что нужно узнать, как связаны между собой данные, каковы отношения между данными и искомыми параметрами. Для этого следует применять моделирование и учить этому детей.

  Цель – изучить теоретические и методологические особенности моделирования при решении текстовых задач в начальной школе.

Достижение этой цели предполагает решение следующих задач:

ü выявить процессы моделирования при генетическом подходе к структуре понятия.

ü теоретически обосновать и показать на примерах интерпретируемость математических моделей.

ü определить этапы моделирования, характер моделей.

1.    Моделирование и его виды.

Моделирование – это:

ü Построение моделей реально существующих объектов (предметов, явлений, процессов);

ü Замена реального объекта его подходящей копией;

ü Исследование объектов познания на их моделях.

При построении моделей используют два принципа:

1.                 дедуктивный (от общего к частному)

При этом подходе рассматривается частный случай общеизвестной фундаментальной модели. Здесь при заданных предположениях известная модель приспосабливается к условиям моделируемого объекта. Например, можно построить модель свободно падающего тела на основе известного закона Ньютона  и в качестве допустимого приближения принять модель равноускоренного движения для малого промежутка времени.

2.                 индуктивный (от частного к общему).

Этот способ предполагает выдвижение гипотез, декомпозицию сложного объекта, анализ, затем синтез. Здесь широко используется подобие, аналогичное моделирование, умозаключение с целью формирования каких-либо закономерностей в виде предположений о поведении системы. Например, подобным способом происходит моделирование строения атома Томсона, Резерфорда, Бора.

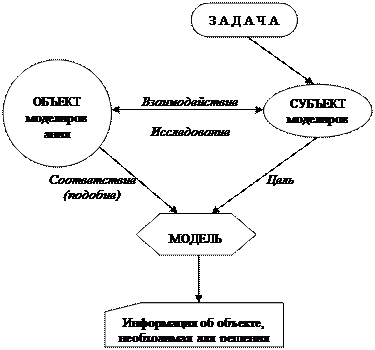Рассмотрим схему построения модели:

^{Рис. 1. Общая схема моделирования}

Выделяют следующие цели моделирования:

ü понимание устройства конкретной системы, ее структуры, свойств, законов развития и взаимодействия с окружающим миром;

ü управление системой, определение наилучших способов управления при заданных целях и критериях;

ü прогнозирование прямых и косвенных последствий реализации заданных способов и форм воздействия на систему.

Виды моделирования

ü концептуальное моделирование, при котором совокупность уже известных фактов или представлений относительно исследуемого объекта или системы истолковывается с помощью некоторых специальных знаков, символов, операций над ними или с помощью естественного или искусственного языков;

ü физическое моделирование, при котором модель и моделируемый объект представляют собой реальные объекты или процессы единой или различной физической природы, причем между процессами в объекте-оригинале и в модели выполняются некоторые соотношения подобия, вытекающие из схожести физических явлений;

ü структурно-функциональное моделирование, при котором моделями являются схемы (блок-схемы), графики, чертежи, диаграммы, таблицы, рисунки, дополненные специальными правилами их объединения и преобразования;

ü математическое моделирование, при котором моделирование, включая построение модели, осуществляется средствами математики и логики;

ü имитационное (программное) моделирование, при котором логико-математическая модель исследуемого объекта представляет собой алгоритм функционирования объекта, реализованный в виде программного комплекса для компьютера.

2. Понятие модели и ее построение.

Понятие «модель» возникло в процессе опытного изучения мира, а само слово «модель» произошло от латинских слов «modus», «modulus», означающих меру, образ, способ. Почти во всех европейских языках оно употреблялось для обозначения образа или прообраза, или вещи, сходной в каком-то отношении с другой вещью.

Чарльз Лейв и Джеймс Марч дают такое определение модели: «Модель – это упрощенная картина реального мира. Она обладает некоторыми, но не всеми свойствами реального мира. Она представляет собой множество взаимосвязанных предположений о мире. Модель проще тех явлений, которые она по замыслу отображает или объясняет» .

·       Т.о. под моделью будем понимать материальный или идеальный объект, который строится для изучения исходного объекта (оригинала) и который отражает наиболее важные (существенные) качества и параметры оригинала.

Модели и моделирование широко представлены в школьной программе. Простейшие математические модели появляются уже в начальных классах при изучении арифметических операций. В дальнейшем количество моделей возрастает, модели усложняются.

К модели предъявляются следующие требования:

·                     модель должна по возможности отображать все основные факторы и взаимосвязи, характеризующие реальные ситуации, критерии и ограничения;

·                     модель должна быть достаточно универсальной, чтобы по возможности описывать близкие по назначению объекты;

·                     модель должна быть достаточно простой, чтобы позволить выполнить необходимые исследования с разумными затратами.

Модели объектов используются для:

·                     представления (репрезентации) материальных предметов;

·                     объяснения известных фактов;

·                     построения гипотез;

·                     получения новых знаний об исследуемых объектах;

·                     прогнозирования;

2.Текстовые задачи и процесс их решения.

Любая текстовая задача представляет собой описание какого-либо явления (ситуации, процесса).  В текстовой задаче описывается не все явление в целом, а лишь некоторые его стороны, главным образом, его количественные характеристики.

Рассмотрим задачу из начального курса математики: «Свитер, шапку и шарф связали из 1 кг 200 г шерсти. На шарф по­требовалась на 100 г шерсти больше, чем на шапку, и на 400 г меньше, чем на свитер. Сколько шерсти израсходовали на каждую вещь?»

В задаче речь идет о расходовании шерсти на свитер, шапку и шарф. Относительно этих объектов имеются определенные утверждения и требования.

Утверждения:

1.Свитер, шапка и шарф связаны из 1200 г шерсти.

2.На шарф израсходовали на 100 г больше, чем на шапку.

3.На шарф израсходовали на 400 г меньше, чем на свитер.

Требования:

1.Сколько шерсти израсходовали на свитер?

2.Сколько шерсти израсходовали на шапку?

3.Сколько шерсти израсходовали на шарф?

Утверждения задачи называют условиями (или условием, как в на­чальной школе). В задаче обычно не одно условие, а несколько элемен­тарных условий. Они представляют собой количественные или каче­ственные характеристики объектов задачи и отношений между ними. Требований в задаче может быть несколько. Они могут быть сформу­лированы как в вопросительной, так и утвердительной форме. Усло­вия и требования взаимосвязаны.

Таким образом, чтобы понять, какова структура задачи, надо вы­явить ее условия и требования, отбросив все лишнее, второстепенное, не влияющее на ее структуру. Иными словами, надо построить высказывательную модель задачи.

Чтобы получить эту модель, надо текст задачи развернуть (сделать это можно письменно или устно), так как текст задачи, как правило, дается в сокращенном, свернутом виде. Для этого можно перефрази­ровать задачу, построить ее графическую модель, ввести какие-либо обозначения и т.д.

Уточним теперь смысл термина «решение задачи».

ü решением задачи называют результат, т.е. ответ на требование

задачи;

ü решением задачи называют процесс нахождения этого результа­та, причем этот процесс рассматривают двояко: и как метод нахожде­ния результата.

4.Моделирование в процессе решения текстовых задач.

Рассматривая процесс решения текстовой задачи, мы неоднократно используем термин «модель», «моделирование»- это неслучайно. Математической моделью текстовой задачи является выражение (либо запись по действиям),если задача решается арифметическим методом, и уравнение (либо система уравнений),если задача решается алгебраическим методом.

1 этап - это перевод условий задачи на математический язык; при этом выделяются необходимые для решения данные и искомые и математическими способами описываются связи между ними;

2 этап - внутри модельное решение (т.е. нахождение значения выражения, выполнение действий решение уравнения);

3 этап - интерпретация , т. е. перевод полученного решения на тот язык, на котором была сформулирована исходная задача.

Задача № 1.  «В одном вагоне электропоезда было пассажиров в два раза больше, чем в другом. Когда из первого вагона вышли 3 человека ,а во 2ой вагон вошли 7 человек, то в обоих вагонах пассажиров стало поровну. Сколько пассажиров было в каждом вагоне первоначально?».

Обозначим через х первоначальное число пассажиров во 2ом вагоне ,тогда число пассажиров в 1ом вагоне - 2х. Когда из 1ого вагона вышли 3 человека, в нём осталось 2х-3 пассажира. Во 2ой вагон вошли 7 человек ,значит, в нём стало х+7 пассажиров .

Т.к. в обоих вагонах пассажиров стало поровну, то можно записать ,что 2х-3=х+7. Получили уравнение - эта математическая модель данной задачи.

Следующий этап  - решение  полученного уравнения вне зависимости от того, что в нем обозначает переменная х:переносим в левую часть  члены уравнения, содержащие х , а в правую – не содержащие х ,при чем у переносимых членов знаки меняем на противоположные: 2х-х=7+3. Приводим подобные члены и получаем, что х=10.

Последний 3ий этап - используем полученное решение, чтобы ответить на вопрос задачи:во2ом  вагоне было первоначально 10 человек ,а в 1ом-20 (10*2=20).Наибольшую сложность в процессе решения текстовой задачи представляет перевод текста с естественного языка на математический, т.е. 1ый  этап математического моделирования.

Чтобы облегчить эту процедуру, строят вспомогательные модели-схемы, таблицы и другое. Тогда процесс решения задачи можно рассматривать как переход от одной модели к другой : от словесной модели реальной ситуации, представленной в задачи ,к вспомогательной(схемы, таблицы ,рисунки и т.д.);

       Задачи в начальной школе.

Задача № 2. Все мальчики класса приняли участие в школьных соревнованиях:      часть вошли в футбольную команду,       часть в баскетбольную,      часть состязалась в прыжках в длину, а 6 остальные — в беге. На какую часть бегунов было больше (меньше), чем футболистов; чем баскет­болистов?

Приведем одно из возможных решений.

Решение

1) -часть мальчиков в футбольной

и баскетбольной командах вместе;

2)часть мальчиков в футбольной, баскетбольной командах и тех, кто состязал­ся в прыжках в длину;

3) часть мальчиков, которые приняли участие в соревнованиях по бегу;

4) на такую часть больше футбо­листов, чем бегунов;

5)на такую часть больше бегу­нов, чем баскетболистов.

Ошибочные решения:

1-й вариант               2-й вариант      

1)          1)      

2)               2)

3)

4)

Обнаруженные ошибки свидетельствуют о том, что ученики не справились с решением задачи, не смогли четко представить себе жизненную ситуацию, отраженную в ее условии, не уяснили от­ношений между заданными величинами и зави­симости между данными и искомыми, а поэтому иногда механически манипулировали числами.

Одна из основных при­чин, по которой дети допускают ошибки в реше­нии текстовых задач, заключается в неграмотной организации работы по первичному восприятию учащимися условия задачи и ее анализа, которая проводятся без должной опоры на жизненную ситуацию, отраженную в задаче, без ее графичес­кого моделирования.

Так, в 4 классе, впервые анализируя условие задачи 2, его кратко записывают примерно в таком виде.

В мат. кр. - 18 уч.

В танц. кр. — ?, на 12 уч. больше, чем в мат. кр.

В спорт, кр. — ?, на 5 уч. меньше, чем в танц. кр.

Такая запись при первичном анализе условия задачи нерациональна, так как не раскрывает на­глядно зависимости между данными и искомыми величинами и не помогает в выборе действия. Мы же предлагаем учащимся модель
            В мат. кр.                                           18 чел.

В танц.кр.                                                    на 12 чел. больше

 В спорт.кр.                                                  на 5 чел. меньше

(Рис. 1)

Можно предложить учащимся найти и другой способ решения, рассмотрев более внимательно ту же модель. Опираясь на графическую схему, дети выясняют: в спортивном кружке учащихся боль­ше, чем в математическом кружке, определяют, на сколько больше (12 — 5 = 7 уч.), а затем уже отве­чают на поставленный вопрос (18 + 7 = 25 уч.).

Как можно смоделировать задачу?

        С помощью схематических чертежей (рис. 2, 3). Такая модель помогает уяснить одно из важ­ных условий задачи, которое вызвало наибольшее затруднение в решении, а именно: после того, как в каждом магазине продали часть завезенного масла, в каждом из них масла осталось поровну.

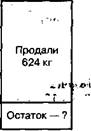
             3840кг

Рис.2

         Графическая модель задачи позволяет преду­предить ошибки в решении. Она также создает предпосылки для активной мыслительной дея­тельности в поисках разных способов решения одной и той же задачи.

Заключение

Моделирование при решении текстовых задач по математике дает возможность развивать познавательную активность обучающихся, интеллектуальные и творческие способности, самостоятельность, прививать интерес к предмету; формировать навыки решения задач.

Данный процесс можно реализовать в традиционной системе обучения при решении математических задач, используя метод моделирования. Он дополняет учебную работу школьников поисковой деятельностью, помогает формированию таких приемов умственной деятельности как абстрагирование, анализ, синтез; развивает математическое мышление.

            Существуют  разные способы проверки решения текстовой задачи. Среди них — решение задачи различными спосо­бами и установление соответствия между полу­ченными в ответе числами и данными числами. Наши наблюдения показывают, что решение задачи, как правило, не проверяют, или понимают под проверкой нечто иное, напри­мер прочтение решения задачи для всего класса или сверку с записью решения на доске.

Проверить правильность ре­шения поможет графическая модель задачи. Та­кую модель можно использовать и для проведе­ния исследования: она помогает выявить условия, при которых задача имеет (или не имеет) реше­ния, найти число решений, выяснить, как изме­няется значение искомой величины в зависимос­ти от изменения данных величин, и т.д.

        Таким образом, была достигнута цель, которую мы ставили: изучить теоретические и методологические особенности моделирования при решении текстовых задач в начальной школе.

Моделирование при решении текстовых задач позволяет младшим школьникам подняться на достаточно высокую ступеньку абстрактности.

Список использованной литературы

Учебники и учебные пособия:

Шевкин А.В. Материалы курса «Текстовые задачи в школьном курсе математики»: Лекции 1-4. – М.: Педагогический университет «Первое сентября», 2006.

Шевкин А.В. Материалы курса «Текстовые задачи в школьном курсе математики»: Лекции 5-8. – М.: Педагогический университет «Первое сентября», 2006.

Математика. 4 класс. Учеб, для общеобразоват. организаций. В 2 ч. Ч. 1 / [М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др.]. — 4-е изд. — М.: Просвещение, 2015.—(Школа России). «Математика. 4 класс»

Периодические издания:

Обучение решению задач как средство развития учащихся: из опыта работы. Методическое пособие для учителя. – Киров, ИИУ. – 1999.

Тоом А.Л. Между детством и математикой: Текстовые задачи в математическом образовании/ Математика, 2005, № 14

Фридман Л.М., Турецкий Е.Н. Как научится решать задачи: Кн для учащихся ст. классов сред. шк. – 3-е изд., дораб. – М.: Просвещение, 1989.

Источники из Интернет

MOODLE КНИТУ. Система образования. Лекция по способам решения текстовых задач. Web: https://moodle.kstu.ru/mod/book/view.php?id=73632&chapterid=17012

Скачано с www.znanio.ru