РЕКУРСИВНЫЕ СТРУКТУРЫ.docx

РЕКУРСИВНЫЕ СТРУКТУРЫ

Рекурсивные структуры являются другим видом повторяющихся структур. Цикл означает повторное выполнение набо- ра команд, при этом весь набор команд полностью выполняется, а затем повторяется. Рекурсия же предполагает повторное выполнение набора команд как подзадачу самой себя. Чтобы ввести понятие рекурсии, рассмотрим алгоритм двоичного по- иска (binary search), в котором в процессе поиска применяется метод разбиения.

Поиск и сортировка. Алгоритмы последовательного и двоичного поиска – это всего лишь два представителя из большого семейст- ва алгоритмов, осуществляющих поисковый процесс. (Использование для этой цели индексов и механизм перемешивания будет рас- сматриваться в главе 8.) Аналогично, сортировка методом вставки – это лишь один из многих существующих алгоритмов сортиров- ки. Другими классическими алгоритмами являются сортировка слиянием (обсуждается в главе 11), выборочная сортировка (ее опи- сание можно найти в подразделе "Вопросы для самопроверки", п. 5 раздела 4.4), сортировка методом пузырька (см. подраздел "Вопросы для самопроверки", п. 6, раздела 4.4), быстрая сортировка (применяющая к процессу сортировки принцип "разделяй и властвуй") и древовидная сортировка (использующая искусную методику для нахождения элементов, которые следует переместить вверх по спи- ску).

Описание этих алгоритмов вы сможете найти в книгах, указанных в списке дополнительной литературы в конце главы. Третий том книги Дональда Кнута "Искусство программирования", хотя и сложен для восприятия начинающими, в целом может считаться последним словом в области методик поиска и сортировки. В своем многотомном труде (который со временем может составить семь томов) Кнут собрал невероятное количество информации, относящейся к фундаментальным алгоритмам вычислений, и тем самым внес значительный вклад в библиотеки специалистов в области компьютерных наук и обработки данных.

Алгоритм двоичного поиска. Давайте вновь рассмотрим задачу поиска заданного элемента в отсортированном списке. Но на этот раз подойдем к этому несколько иначе. Попытаемся использовать процедуру, которой мы обычно следуем при поиске имени в телефонном справочнике. Человек никогда не просматривает справочник последовательно, элемент за эле- ментом или даже страница за страницей. Мы просто открываем его примерно в том месте, где, как мы думаем, может нахо- диться нужное имя. Если повезет, оно окажется именно там, в противном случае поиск придется продолжить. Однако в этой точке мы уже сузим область поиска либо до начальной части справочника, предшествующей нашей текущей позиции, либо до остальной части справочника, следующей за ней.

На рис. 4.12 этот подход, применяемый к произвольному отсортированному списку, описан с помощью псевдокода. В данном случае мы не знаем примерного места расположения элементов, поэтому инструкции на рисунке предписывают на- чинать работу с открытия списка на "среднем" элементе. Слово "средний" заключено в кавычки, поскольку вполне возмож- но, что число элементов в списке будет четным, и тогда среднего элемента в строгом смысле этого слова просто не сущест- вует. В этом случае условимся, что средним считается первый элемент второй половины списка.

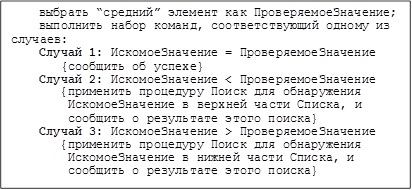Рис. 4.12. Принцип двоичного поиска

Если выбранный элемент не является искомым, то программа, приведенная на рис. 4.12, предлагает два варианта даль- нейших действий (поиск или в начальной или конечной половине списка). В каждом из них предусматривается выполнения вторичного поиска, осуществляемого процедурой с именем Search. Следовательно, чтобы завершить нашу программу, не- обходимо создать подобную процедуру, описывающую, как осуществляется этот вторичный поиск. Заметим, что эта проце- дура должна быть в состоянии удовлетворить запрос на поиск в пустом списке. Например, если показанной на рис. 4.12 про- грамме будет передан список, состоящий из одного элемента, который не является искомым, то процедура Search будет вызвана для поиска либо в подсписке, находящемся выше этого единственного значения, либо в подсписке, находящемся ниже его, однако оба эти списка пусты.

В качестве искомой процедуры Search можно было бы использовать процедуру последовательного поиска, созданную нами в предыдущем разделе, но это совсем не тот метод, который выбрал бы человек при поиске в телефонном справочнике. Вероятно, он просто применил бы к оставшейся части справочника ту же процедуру, которой только что воспользовался для всего справочника в целом. Другими словами, выбрал бы какой-то элемент, достаточно близкий к середине оставшейся части спи-

ска, и использовал его для дальнейшего сужения области поиска.

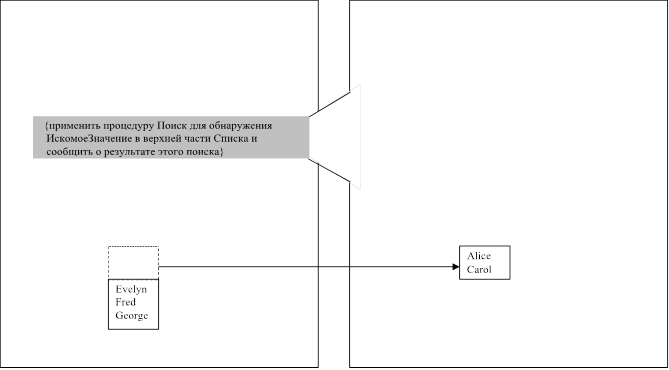
Подобный подход к процедуре поиска представлен на рис. 4.13. Здесь демонстрируется способ решения задачи, заклю- чающейся в определении присутствия имени John в списке, приведенном в левой части рисунка. Прежде всего, анализирует- ся средний элемент Harry. Так как имя, которое мы ищем, по алфавиту располагается после данного имени, поиск продолжа- ется в нижней части исходного списка. Средним элементом этой части является имя Larry. Поскольку по алфавиту искомое имя предшествует данному, поиск следует продолжать в верхней части текущего подсписка. Обратившись к среднему эле- менту этого вторичного подсписка, обнаруживаем искомое имя John и объявляем поиск успешным. Короче говоря, наша стратегия состоит в последовательном делении анализируемого списка на меньшие по размеру сегменты до тех пор, пока либо будет найдено искомое значение, либо поиск сузится до пустого сегмента.

Можно реализовать эту стратегию с помощью нашего псевдокода, модифицировав приведенную на рис. 4.12 программу так, чтобы учесть возможность получения пустого списка. Модифицированная соответствующим образом программа на псевдо- коде, которой присвоено имя Search, показана на рис. 4.14. При выполнении этой процедуры и при достижении инструк- ции "Применить процедуру Search, чтобы ...", мы будем просто применять этот же метод поиска к меньшему списку, который является частью исходного списка. Если этот вторичный поиск завершится успешно, мы вернемся в исход- ную процедуру, чтобы объявить выполняемый в ней поиск успешным. Если же вторичный поиск окончится неудачей, мы объявим неудачным и исходный поиск.

Исходный

  список Alice Bob Carol David Elaine Fred George

Первый подсписок

Второй подсписок

Irene                   Irene                  Irene

John                   John

Kelly                  Kelly                  Kelly Larry

Mary                  Mary

Nancy                 Nancy

Oliver                 Oliver

Рис. 4.13. Применение стратегии двоичного поиска для обнаружения имени John в упорядоченном списке

Чтобы увидеть, как представленная на рис. 4.14 процедура выполняет свою задачу, попробуем с ее помощью опреде- лить, содержится ли значение Bill в списке имен Alice, Bill, Carol, David, Evelyn, Fred, George. Поиск начинается с выбора в качестве проверяемого элемента имени David (среднего элемента списка). Так как искомое значение (Bill) по алфавиту предшествует проверяемому, следует применить процедуру Search к списку элементов, предшествующих имени David, т.е. к списку Alice, Bill, Carol. Для этого нам потребуется создать

Рис. 4.14. Алгоритм двоичного поиска, записанный на псевдокоде

вторую копию процедуры Search, предназначенную для решения данной промежуточной задачи.

Теперь мы имеем две выполняющиеся копии нашей процедуры поиска, как показано на рис. 4.15. Дальнейшее выполне- ние исходной копии процедуры временно приостановлено на следующей инструкции:

Применить процедуру Search, чтобы определить, есть ли в части списка, предшествующей элементу <проверяемый_элемент>, элемент <искомое_значение>

Вторая копия процедуры используется для поиска имени Bill в списке Alice, Bill, Carol. Завершив вторую процедуру двоичного поиска, мы аннулируем ее копию и сообщим полученные в ней результаты исходной копии, после чего выполне- ние исходной копии будет продолжено с указанного места. Таким образом, вторая копия процедуры функционирует как подчиненная исходной, выполняя задачу, запрошенную исходной копией, а затем исчезая.

Вторичная процедура поиска выбирает имя Bill в качестве проверяемого значения, так как это средний элемент в списке Alice, Bill, Carol. Поскольку он совпадает с искомым значением, поиск объявляется успешным и вторичная процедура за- вершает свою работу.

Procedure Поиск (Список, ИскомоеЗначение)

if (Список пустой)

then {сообщить о неудаче}

else {выбрать “средний” элемент как ПроверяемоеЗначение; выполнить набор команд, соответствующий одному

из случаев:

Случай 1: ИскомоеЗначение = ПроверяемоеЗначение

{сообщить об успехе}

Случай 2: ИскомоеЗначение < ПроверяемоеЗначение

Случай 3: ИскомоеЗначение > ПроверяемоеЗначение

{применить процедуру Поиск для обнаружения ИскомоеЗначение в нижней части Списка и сообщить о результате этого поиска}

Procedure Поиск (Список, ИскомоеЗначение)

if (Список пустой)

then {сообщить о неудаче}

else {выбрать “средний” элемент как ПроверяемоеЗначение; выполнить набор команд, соответствующий одному

из случаев:

Случай 1: ИскомоеЗначение = ПроверяемоеЗначение

{сообщить об успехе}

Случай 2: ИскомоеЗначение < ПроверяемоеЗначение

{применить процедуру Поиск для обнаружения ИскомоеЗначение в верхней части Списка и сообщить о результате этого поиска}

Случай 3: ИскомоеЗначение > ПроверяемоеЗначение

{применить процедуру Поиск для обнаружения ИскомоеЗначение в нижней части Списка и сообщить о результате этого поиска}

}                          Список                                                                            }                          Список

Рис. 4.15. Вызов второй копии процедуры из ее исходной копии при поиске записи Bill

Procedure Поиск (Список, ИскомоеЗначение)

if (Список пустой)

then {сообщить о неудаче}

else {выбрать “средний” элемент как ПроверяемоеЗначение; выполнить набор команд, соответствующий одному

из случаев:

Случай 1: ИскомоеЗначение = ПроверяемоеЗначение

{сообщить об успехе}

Случай 2: ИскомоеЗначение < ПроверяемоеЗначение

Случай 3: ИскомоеЗначение > ПроверяемоеЗначение

{применить процедуру Поиск для обнаружения ИскомоеЗначение в нижней части Списка и сообщить о результате этого поиска}

}

Список

Procedure Поиск (Список, ИскомоеЗначение)

if (Список пустой)

then {сообщить о неудаче}

else {выбрать “средний” элемент как ПроверяемоеЗначение; выполнить набор команд, соответствующий одному

из случаев:

Случай 1: ИскомоеЗначение = ПроверяемоеЗначение

{сообщить об успехе}

Случай 2: ИскомоеЗначение < ПроверяемоеЗначение

{применить процедуру Поиск для обнаружения ИскомоеЗначение в верхней части Списка и сообщить о результате этого поиска}

Случай 3: ИскомоеЗначение > ПроверяемоеЗначение

{применить процедуру Поиск для обнаружения ИскомоеЗначение в нижней части Списка и сообщить о результате этого поиска}

}

Список

Рис. 4.16. Вызов второй копии процедуры из ее исходной копии при поиске записи David

На этом этапе мы завершили дополнительный поиск, как предписывалось исходной процедурой, поэтому можно продол- жить выполнение этой исходной копии, т.е. объявить результат дополнительного поиска результатом первоначального поис- ка. В итоге выполнения всего процесса было совершенно справедливо установлено, что имя Bill присутствует в списке имен Alice, Bill, Carol, David, Evelyn, Fred, George.

Теперь давайте посмотрим, что произойдет, если перед представленной на рис. 4.14 процедурой поставить задачу опре- делить наличие в списке Alice, Carol, Evelyn, Fred, George элемента David. На этот раз исходная копия процедуры выбирает в качестве проверяемого значения имя Evelyn и определяет, что искомое значение должно находиться в предшествующей час- ти списка. Поэтому она вызывает еще одну копию процедуры для поиска в списке тех элементов, которые стоят перед име- нем Evelyn, т.е. в двухэлементном списке, состоящем из имен Alice и Carol. Ситуация на этой стадии выполнения алгоритма представлена на рис. 4.16.

Вторая копия процедуры выберет в качестве проверяемого элемента имя Carol и определит, что искомое значение должно находиться после него. Процедура вызовет третью копию процедуры "Поиск" для поиска требуемого элемента в списке имен, следующих за именем Carol в списке Alice, Carol. Однако этот список пуст и перед третьей копией процедуры стоит задача поиска искомого значения David в пустом списке. Исходная копия процедуры осуществляет поиск требуемого элемента в списке Alice, Carol, Evelyn, Fred, George, выбрав в качестве проверяемого имя Evelyn; вторая копия процедуры занята поиском требуемого элемента в списке Alice, Carol, выбрав в качеству проверяемого элемент Carol; а третья начинает поиск в пустом списке.

Конечно же, третья копия процедуры тут же объявляет свой поиск неудачным и завершается. После этого вторая копия может продолжить свою работу. Она обнаруживает, что запрошенный поиск оказался неуспешным, поэтому также объявля- ет свой поиск неудачным и завершается. Исходная копия процедуры, ожидавшая поступления сообщения от второй копии, теперь может продолжить свою работу. Так как запрошенный поиск оказался неудачным, она тоже объявляет свой поиск неудачным, после чего завершается. Таким образом, наша программа пришла к правильному заключению, что имя David не содержится в списке имен Alice, Carol, Evelyn, Fred, George.

Если еще раз просмотреть приведенные выше примеры, можно увидеть, что в процессе, осуществляемом представлен- ным на рис. 4.14 алгоритмом, необходимо многократно разделять рассматриваемый список на две примерно равные части, после чего область дальнейшего поиска ограничивается лишь одной из этих частей. Именно это повторяющееся деление на два послужило причиной того, что данный алгоритм был назван двоичным поиском.

Управление рекурсией. Алгоритм двоичного поиска похож на алгоритм последовательного поиска, так как каждый из них предусматривает выполнение повторяющегося процесса. Однако реализация этого повторения в каждом случае существенно от- личается. При последовательном поиске повторение организуется с помощью цикла, в случае двоичного поиска каждая стадия повторения реализуется как подзадача предыдущей стадии. Этот метод повторения известен как рекурсия (recursion).

При выполнении рекурсивного алгоритма создается иллюзия существования множества его копий, называемых акти- вациями (activation), которые появляются и исчезают по мере выполнения алгоритма. Из всех активаций, существующих в заданный момент времени, активно функционирует только одна. Все остальные фактически остановлены, поскольку каждая из них ожидает, пока завершится следующая, запущенная ею активация, и только после этого она сможет продолжить свою работу.

Будучи повторяющимися процессами, рекурсивные структуры почти так же зависят от корректного управления, как и циклические структуры. Как и в случае управления циклами, рекурсивные системы зависят от проверки условия окончания

и должны разрабатываться так, чтобы иметь гарантии, что это условие будет обязательно выполнено. Фактически правильно организованное управление рекурсией включает те же три операции, что и управление циклом, – инициализация, модифика- ция и проверка условия окончания.

Разработка рекурсивных процедур. При создании рекурсивных процедур основным условием является выбор способа, с помо- щью которого исходную задачу можно разделить на меньшие задачи того же типа, а также определить, как результаты решения этих меньших задач могут быть использованы в качестве абстрактных инструментов нахождения решения исходной задачи. Давайте при- меним этот подход к поиску выхода из лабиринта, подобного приведенному на этом рисунке. Будем продвигаться вперед до тех пор, пока не подойдем к первому разветвлению. В этой точке мы будем считать, что каждый вариант дальнейшего движения представляет собой вход в новый лабиринт меньшего размера. Если в любом из этих меньших лабиринтов выход будет найден, наша задача реше- на. Такой способ рассуждений приводит к построению следующей процедуры:

procedure FindExit (<лабиринт>)

Продвигаться по лабиринту до развилки, тупика или выхода; В каждом из указанных случаев вы- полнить соответствующие инструкции из числа приведенных ниже:

case 1: достигнут выход: (сообщить "выход найден")

case 2: достигнут тупик: (сообщить "неудача")

case 3: достигнута развилка:

(while       (есть       ветвь,       ведущая       к       неисследованной       территории, и выход еще не найден) do

(применить процедуру FindExit к лабиринту, представленному одной из неисследованных ветвей;

if (эта процедура сообщила, что выход найден)

then (сообщить "выход найден".)

)

if (все варианты этой развилки неудачны)

then (сообщить "неудача")

Обычно рекурсивная программа разрабатывается так, чтобы проверять условие окончания (часто называемое гранич- ным условием, или условием вырождения) до того, как будут вызваны последующие активации. Если условие окончания еще не достигнуто, то программа создает следующую свою активацию, задача которой – найти решение сокращенной версии задачи текущей активации. Подразумевается, что эта сокращенная версия находится ближе к условию окончания, чем зада- ча, которой занимается текущая активация. Как только условие окончания будет обнаружено, выбирается путь, вызывающий завершение текущей активации без создания дополнительных активаций. Это означает, что одной из остановленных актива- ций разрешается продолжить свое выполнение, завершить ее задачу и, в свою очередь, позволить следующей остановленной активации возобновить свои действия. Таким образом, все порожденные активации в конечном счете будут завершены, что приведет к завершению исходной задачи.

Теперь посмотрим, как операции инициализации и модификации механизма управления повторением реализованы в рекур- сивной программе двоичного поиска (рис. 4.14). В этом случае создание дополнительных активаций прекращается, когда обнару- живается искомое значение или задача сужается до поиска в пустом списке. Процесс инициализируется неявно, посредством зада- ния исходного списка и искомого значения. Начиная с этой конфигурации, программа модифицирует свою задачу, что приво- дит к поиску во все уменьшающемся списке. Поскольку длина исходного списка конечна, а каждый этап модификации уменьшает длину рассматриваемого списка, можно гарантировать, что либо искомое значение будет найдено, либо задача сузится до поиска в пустом списке. Следовательно, можно сделать заключение, что процесс повторения гарантированно прекратится.

Рассматривая структуры управления рекурсией и итерациями, можно попробовать установить, одинаковы ли их воз- можности. То есть, если некоторый алгоритм разработан с использованием циклической структуры, то можно ли для реше- ния этой же задачи разработать другой алгоритм, применяющий только рекурсивные методы, и наоборот. Такие вопросы важны с точки зрения компьютерных наук, так как ответы на них позволяют понять, какие функции необходимо реализовать в языке программирования, чтобы получить как можно более мощную систему разработки программ. Мы вернемся к этой проблеме в главе 11, где будут рассматриваться некоторые теоретические аспекты компьютерных наук и их математических основ. Опираясь на сделанные в этой главе выводы, в приложении Д будет доказана эквивалентность итеративных и рекур- сивных структур.

Вопросы для самопроверки

1.    Какие имена будут проверены программой двоичного поиска (рис. 4.14) при поиске имени Joe в списке имен Alice, Bob, Carol, David, Evelyn, Fred, George, Henry, Irene, Joe, Karl, Larry, Mary, Nancy и Oliver?

2.    Какое максимальное количество элементов может потребоваться проверить при выполнении двоичного поиска в списке из 200 элементов? В списке из 100 000 элементов?