УДК 378

ББК 74

А287

 

Алексеевская Л. Е.

                   И        Решай визуализируя и выбирай профессию на уроках ма-

 А287     тематики. Учебное пособие. – Куйбышев : КФ ФГБОУ ВО «НГПУ», 2018. – 48 с.

 

ISBN 978-5-ХХХХХХ-ХХ-Х

 

  

 

Рецензент: Н. П. Шаталова, доцент, кандидат физикоматематических наук, профессор РАЕ, профессор кафедры МИиМП, Новосибирский государственный педагогический университет (Куйбышевский филиал), г. Куйбышев 

Рецензент: Щербакова Надежда Алексеевна, учитель математики высшей квалификационной категории МБОУ СОШ №3 Куйбышевского района Новосибирской области.

 

 Учебное пособие представляет комплекс задач профессионального контекста, решение которых возможно с использованием визуальных моделей. В пособии представлены математические задачи, которые можно использовать на уроках математики в 9 классе.

Издание предназначено для обучающихся и учителей общеобразовательных школ. 

 

 

 

УДК 378

ББК 74

 

        

         ISBN978-5-ХХХХХХ-ХХ-Х               © Куйбышевский филиал КФ ФГБОУ ВО

«НГПУ», НИЛ КО КФ ФГБОУ ВО «НГПУ», 2018

© Алексеевская Л. Е., 2018  

 

 

ОГЛАВЛЕНИЕ

 

 

ВВЕДЕНИЕ.................................................................. 4

ЗАДАЧИ, ПРИ РЕШЕНИИ КОТОРЫХ ТРЕБУЕТСЯ ПРИМЕНЕНИЕ СТАТИЧЕСКИХ  ВИЗУАЛЬНЫХ     ............................

МОДЕЛЕЙ.................................................................... 6

ЗАДАЧИ, ПРИ РЕШЕНИИ КОТОРЫХ ТРЕБУЕТСЯ   ПРИМЕНЕНИЕ ДИНАМИЧЕСКИХ ВИЗУАЛЬНЫХ .............................

МОДЕЛЕЙ.................................................................. 12

РЕШЕНИЕ  ЗАДАЧ  ПРОФЕССИОНАЛЬНОГО ..........

СОДЕРЖАНИЯ.......................................................... 17

МЕТОДИЧЕСКИЕ  РЕКОМЕНДАЦИИ  К ...................

ОРГАНИЗАЦИИ УЧЕБНОЙ ДЕЯТЕЛЬНОСТИ ПРИ РЕШЕНИИ ЗАДАЧ 34

ОТВЕТЫ К ЗАДАЧАМ.............................................. 42

СПИСОК РЕКОМЕНДОВАННОЙ ЛИТЕРАТУРЫ... 44

 ДИСК С ПРЕЗЕНТАЦИЯМИ.................................... 46

 

 

ВВЕДЕНИЕ

 

 

В процессе знакомства с профессией через математические задачи требуется умение  осуществлять процесс моделирования. Сегодня образовательные школы имеют возможность использовать в обучении школьников различные виды визуальных моделей: операционные, формализованные, структурные, эвристические,  дистрибутивные, визуальные модели преемственности. 

Сама теория моделирования рассматривает две группы способов моделирования: аналитическое и имитационное. 

Под аналитическим моделированием понимают построение модели, основанной на описании поведения объекта или системы объектов в виде аналитических выражений – формул. При таком моделировании объект описывается геометрическими формулами, алгебраическими уравнениями, неравенствами, решение которых может дать представление о свойствах объекта, описанного в задаче. 

Имитационное моделирование предполагает построение модели с характеристиками, адекватными оригиналу, на основе какого-либо его физического или информационного принципа. Это означает, что внешние воздействия на модель и объект вызывают идентичные изменения свойств оригинала и модели. В последнее время имитационное моделирование все больше реализуют моделированием объектов на компьютере, что позволяет в  интерактивном режиме исследовать модели самых разных по природе объектов.

 «Многогранники и тела вращения» – одна из важнейших тем в курсе геометрии девятого класса. Прикладная направленность данной темы обуславливается применением ее в различных профессиях. Однако, не секрет, что её изучение вызывает затруднение у большинства обучающихся. Повысить интерес к математике, к данной теме и к выбору профессии поможет данное учебное пособие. 

Учебное пособие содержит задачи по теме «Многогранники и тела вращения», методические комментарии, презентации к задачам и видео-зарисовки рабочих фрагментов деятельности  специалиста той профессии, о которой идет речь в содержании математической задачи. 

Особенность учебного пособия заключается в том, что оно содержит задачи, в которых учтено соответствие вида визуальной модели и геометрической фигуры. Решение каждой задачи предусматривает свой алгоритм использования визуальной модели.  

             

ЗАДАЧИ,  ПРИ РЕШЕНИИ КОТОРЫХ ТРЕБУЕТСЯ

ПРИМЕНЕНИЕ СТАТИЧЕСКИХ                                   

ВИЗУАЛЬНЫХ  МОДЕЛЕЙ 

 

 

 

 

В данном параграфе предлагается решить задачи средствами статистических визуальных моделей.  

Средства статистической визуализации применяются как инструмент для решения большого круга учебно-методических задач. Они обладают определенными дидактическими возможностями, что позволяет:

-           зафиксировать кадр для обозрения слушателям;

-           регулировать темп демонстрации кадров диафильма;

-           обеспечить демонстрацию нарастающего потока информации;

-           включать зрительную память в систему усвоения знаний, формирования навыков и умений;

-           на кадре диафильма нести большую учебную информацию, чем кадр фильма, так как он освобожден от второстепенных сведений и дополнен текстом;

-           применять графопроекторы на занятиях без затемнения аудитории;

-           развивать интерес слушателей к содержанию через красочное изображение и четкую систему построения материала на слайдах.

Следует отметить, что диафильмы, диапозитивы, слайды, кодопозитивы просты в изготовлении, что доступно практически каждому преподавателю. Они компактнее других наглядных пособий и удобнее в хранении.

Слайды и кодопозитивы удобнее диафильмов, так как их можно быстро подобрать для конкретного занятия, легче обновлять и совершенствовать. Можно изготавливать слайды типа «динамический плакат», в которых последовательно изображаются стадии развития какого-либо процесса. Кроме того слайды позволяют управлять демонстрацией изображения с учетом дидактической целесообразности. Преподаватель может закрыть часть материала черной бумагой, куском картона, фанеры, а затем постепенно открывать, демонстрируя отдельные элементы цельного слайда.

 

Задача 1 (профессии: инженер-строитель, сметчик, экономист) 

Здание игрового центра в форме прямой призмы, в основании которой лежит равнобедренная описанная около бассейна (окружности) трапеция ABCD с боковой стороной, равной 5, и высотой, равной 3, высота здания 20 м. 

Определите, сколько облицовочных плит, размером 0,5 м.

на 0,5 м. нужно закупить для обшивки лицевой стороны здания, если оно расположено так, что лицевая сторона – это сторона, опирающаяся на большее основание трапеции. 

 

Задача 2 (профессия: боксер, реставратор). 

Для тренировки в боксерском клубе используются «спортивные груши». Диаметр «груши» составляет 100 см, а её высота – 90 см. Сколько  квадратных метров ткани понадобится для реставрации спортивной «груши».

 

Задача 3 (профессия: тренер) 

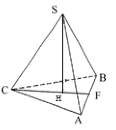
В тренажёрном зале находится снаряд в виде пирамиды. Основанием пирамиды является равнобедренный треугольник с углом 120° и боковой стороной 5 см. Высота пирамиды равна 6 см.  Для того, что бы распределить равномерно нагрузку необходимо определить ее объем.

 

Задача 4 (профессии: мелиоратор)

Используя опорную схему известного учителя-методиста

В. Ф. Шаталова, представленную на рисунке, определить площадь, занятую посевами пшеницы, которая может быть полита водой из цистерны в виде правильной шестиугольной призмы, если сторона ее основания равна 6 м, высота 5 м, а расход воды на 1 кв. м. посевов составляет 10 л. воды.

 

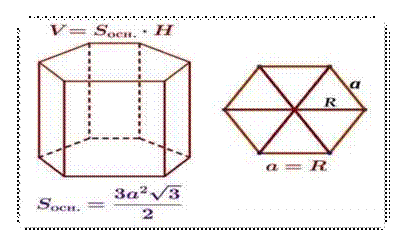
Рисунок 1. Опорная схема по В.Ф. Шаталову

 

Задача 5 (профессия: дизайнер)

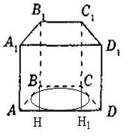
На фабрике шьют платья, которые по форме составляют правильный параллелепипед без нижнего основания. 

Найдите длину выреза под горло на средней линии верхнего основания, если он относится к длине стороны его основания так же как 1:3, высота платья равна 160 см, а его объём равен 156000 см²

 

Задача 6 (профессия: коллекционер)

Была потеряна раритетная вещь. О ней известно только то, что прямоугольник, стороны которого равны 6 см и 4 см, вращается около меньшей стороны. 

Необходимо найти площадь поверхности данной вещи.

 

Задача 7 (профессия: маляр)

При покраске стен рабочие решили прикрыть волосы колпаком в виде конуса радиус основания 12 см. 

Найдите площадь боковой поверхности, если высота конуса равна 16 см.

 

Задача 8 (профессия: спортсмен) 

Мяч для гимнастики с радиусом в 30 см расположен в ящике объемом 114 м³. 

Какое максимальное количество мячей может поместиться в данный ящик?

 

Задача 9 (профессия: повар)

В бочке цилиндрической формы налили 1200 см³ компота. Уровень жидкости оказался равным 15 см. В компот погрузили ягоды от этого компота. 

При этом уровень жидкости в сосуде поднялся на 12 см.

Чему равен объем ягод?

 

Задача 10 (профессия: повар-кондитер) 

Повару-кондитеру поступил заказ на пирожное в виде треугольной призмы в основании которой лежит равнобедренный треугольник с боковой стороной равной 5 см и основанием равным 6 см, для наполнения его малиной необходимо рассчитать объем пирога, если боковое ребро равно 10 см.

 

             

ЗАДАЧИ, ПРИ РЕШЕНИИ КОТОРЫХ ТРЕБУЕТСЯ  

ПРИМЕНЕНИЕ  ДИНАМИЧЕСКИХ                               

ВИЗУАЛЬНЫХ МОДЕЛЕЙ

 

 

 

В данном параграфе предлагается решить задачи средствами дидактических визуальных моделей.  

Средства динамической визуализации по своим педагогическим характеристикам схожи с автоматизированными телевизионными установками. Главное их достоинство заключается в присущей им динамичности представления явлений и процессов. Причем динамика может быть представлена в любом объеме. Средствами кино и телевидения можно представить как отдельное явление, процесс, так и объект в целом и по частям увеличенном размере статично и в динамике.

Продуманность сценария и текста обеспечивает четкость, ясность, лаконичность, убедительность демонстраций, возможность передать большой объем информации в сжатые сроки. Кино и телевидение позволяют интенсифицировать учебный процесс и обеспечить как раскрытие теоретических вопросов, так и решение практических задач.

Основная трудность использования кино и телевидения з ключается в частом отсутствии содержательных, строго отвечающих темам и учебным дисциплинам фильмов. Поэтому необходимо снимать учебные видеофильмы по собственным сценариям.

 При создании учебных видеофильмов рекомендуется:

-  избегать увлечения только внешней эффективностью, повышать их учебную ценность, поучительность;

-  располагать материал логично, полно, всесторонне и последова-тельно освещая тему;

-  не допускать чрезмерного количества разнородных мыслей, давать время усваивать и запоминать их.

 

Задача 11 (профессия: архитектор) 

На ЭКСПО – 2017 павильоны с выставками были расположены в здании в виде стометровой сферы. 

Определите объем данного здания и площадь его поверхности.

 

Задача 12  (профессия: фармацевт)

Больному прописали принимать препарат в пакетиках.

Пакетик выглядит как пирамида наполненная полностью лекарством. Основанием пирамиды является треугольник со сторон ми 12 см, 10 см и 10 см. Высота пирамиды 7 см. 

Найдите объем пирамиды и рассчитайте дозировку приема лекарства в пакетиках, если необходимо принимать по 50 см³.

 

Задача 13  (профессия: археолог) 

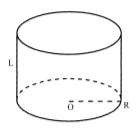
На раскопках была обнаружена загадочная шкатулка в виде прямого цилиндра. Длина окружности основания равна 10 см, длина образующей равна 7 см. 

Чему равна площадь боковой поверхности найденной шкатулки?

 

Задача 14 (профессия: архитектор). 

Разработали здание в виде конуса. Потолок пересечен плоскостью, параллельной основанию, на расстоянии 2 м от вершины. 

Найдите площадь потолка, если радиус основания конуса

8 м, а высота 12 м.

 

Задача 15  (профессия: программист)

На языке программирования требуется написать программу, которая после запуска будет изображать на экране прямой параллелепипед со сторонами основания 8 и 9 см, диагон лью меньшей грани равной 12. 

После написания данной программы необходимо найти диагональ полученного параллелепипеда.

 

Задача 16 (профессия: экономист)

Требуется рассчитать сумму, которую необходимо выделить на то, чтобы застелить пол в здании в форме правильной четырехугольной призмы, при этом известна сторона основания равная 6 м, если материал площадью 6 м² стоит 50 рублей.

 

Задача 17 (профессия: инженер-механик)

В турбине самолета необходимо заменить воду в детали в форме прямого параллелепипеда. Так как видна только часть детали, нужно рассчитать ее объем для замены жидкости, измерив длину одной стороны основания равную 5 см, диагонали основания 8 см и высоты детали равной 14 см.

 

Задача 18  (профессия: звукооператор)

Организатор концертов разрабатывает новый вид аудиопередатчиков высокой мощности в виде правильной прямой пирамиды. Основанием пирамиды является прямоугольник, диаго-

наль которого равна 8 см, а высота пирамиды 5 см. Найдите объём пирамиды.

 

Задача 19 (профессия: художник)

Человеку поручили расписать здание в виде конуса. Высота конуса 12 м и радиус основания равен 8 м. 

Сколько краски понадобится, если покрыть его боковую поверхность, если краска ложится плотным слоем и на 1 м² необходимо затратить 4 литра различной краски.

 

Задача 20 (профессия: врач)

Пациенту прописывают ряд медикаментов, среди которых находятся таблетки в виде шара объемом 32 мм³, при условии что π=3. 

Найдите радиус данных таблеток.

             

РЕШЕНИЕ ЗАДАЧ

 ПРОФЕССИОНАЛЬНОГО СОДЕРЖАНИЯ

 

Задача 1  Дано 

AB=CD=5м;

BH=3м’

AA₁=20м;

0,5×0,5;

 

Найти:

SAA1D1D-?

Решение:

1)   В трапецию можно вписать окружность тогда, и только тогда когда суммы длин её противоположных сторон равны. То есть AB+CD=BC+AD;

2)   AD=AH+HH₁+H₁D, причем AH=H₁D так как CH₁ высота трапеции BC=HH₁;

3)   AH=5²-3²=4 по теорема Пифагора из △ABH;

4)   из (2) и (3) следует, что   AD=8+x,  BC=x;

5)   из (1) следует, что   5+5=8+x+x, найдем сторону 

BC=x:  10=8+2x;  

2=2x;   х=1;

6)   получим AD=8+1=9;

7)   найдем S_AA1D1D=ab=20·9=180 (м²);

8)   S_од.пл.=0,5∙0,5=0,25м²;

9)   180:0,25=720;

Ответ: S_AA1D1D=180 м²; количество – 720.

 

Задача 2 

 

Дано:

ОR=50 см;

L=90 см;

Найти:

S_бок-?  

 

Решение:

1)      S_бок=2∙π∙R∙l;

2)      S_бок=2∙3,14∙ 50 ∙ 90 =28260 см²;

Ответ: S_бок=28260 см²

 

Задача 3

 

Дано:

AC=CB=5; SH=6;

∠ACB=120^о;

Найти:  

V-?

Решение:

a. V=S_осн∙h ,    S_осн ,

2)      из рассмотрения △ABC, следует:

a. ^o,

3)      из рассмотрения △AСH_{1 ,} следует:

СH₁=2,5;

4)      AH;

5)      AB=2∙AH₁=10√0.75=√75=5√3;

6)      S_осн      2,5=6,25√3;

7)      V=6,25√3 ∙6=37,5√3.

Ответ: 37.5√3

Задача 4 

 

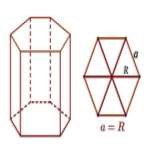Дано:

ABCDEFA₁B₁C₁D₁E₁F₁ – правильная призма;

АВ=6 м;

АА1=5 м;

10 л на 1 м².  

Найти:

S_пос-?

Решение:

1)      S_осн; a=R;

S_осн;

2)      V=S_осн∙h;

V=54√3 ∙ 5 = 270√3;

3)      S_пос;

S_пос;

Sпос=27√3.

Ответ: 27√3.

Задача 5 

 

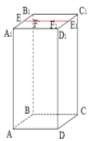Дано:

V=156000 см²;

АА₁=160 см;

Найти:

FF₁-?

 

1)      V=S_осн∙h;

           156000=S_{ос н}∙160;

           S_осн=975;

2)      Так как призма правильная, то АВ=ВС, то есть:

Sосн=АВ2;

975=AB²;

AB=5√39;

3)      EE₁=AB;

EE₁=5√39;

4)      FF.

Ответ: .

 

Задача 6 

 

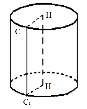Дано:

HH₁=4см;

HC=6см;

Найти: S_полн-?

 

 

                                                         Решение:

 

1  .  S_полн=2 𝜋R(R+H);

2  . S_полн=2∙ 𝜋 ∙HC(HC+HH₁);

3  . S_полн=2 ∙3.14∙6(6+4)=12∙3.14∙10=376.8;

 

Ответ: 376,8

 

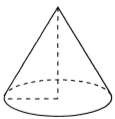Задача 7 Дано:

DH=16см;

HC=12см;

Найти: S_бок-?

 

 

Решение:

1    .  S_бок= 𝜋𝑟²l;

2    .  S_бок= 3.14 ∙12∙BC;

3    .  BCсм;

4    . S_бок=3,14∙12∙20=753,6см²;

Ответ:753,6см²

 

Задача 8

 

Дано:

OR=30см

V_ящ=114 см³ Найти:

Количество мячей в ящике 

 

Задача 9

 

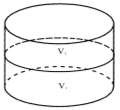Дано:

Цилиндр V₁=1200 см³; h₁=15 см;

 

h₂= 12 см;

Найти: V₂- ?

Решение:

1)        V=πR²H;  

2)        V₁=πR²*15;  

3)        1200= πR²15;  

4)        πR²=80;

5)        V₂= πR²h₂;   

6)        V₂= 8012;      

7)        V₂=960 см³

Ответ: V₂=960 см³

 

Задача 10

 

Дано:

AB=BC= 5см;

AC= 6 см;

AA₁=10см;

Найти: V-?

 

 

Решение:

1  .  V_осн=h;

2  .  S_оснc;

    S_оснBH;

   BH =4см;

.  S_осн 6=12см²;

3  .  V=12∙10=120 см²;

Ответ: 120 см²

 

Задача 11 

 

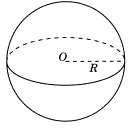Дано:

Сфера;

D – диаметр;

D=100 м;

Найти: 

V-?

S-?

Решение:

;

𝑆 = 4 ∙ 𝜋 ∙ 𝑟²;

1.      так как , то r= 50 м;

2.      за π возьмем 3,14. 

3.

;

4.  𝑆 = 4 ∙ 𝜋 ∙ 𝑟² = 4 ∙ 3,14 ∙ 50² = 4 ∙ 3,14 ∙ 2500 =     =

31400 (м²);

Ответ: ;

      𝑆 = 31400 (м²)/

 

Задача 12

 

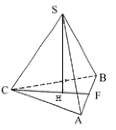Дано:

Пирамида;

AС=BС=10см;

AВ=12см;

H=7см;  

Найти 

V и  дозировку.        

Решение:

1)      V = S_осн∙h;

2)      S_осн BH;

3)      BH=√100 − 36=8;

4)      S_осн;

5)      V=48∙7=336 см³;

6)      336:50=6,72 (дозировка на 1 пакетик).

Ответ: V=336см³ дозировка=6,72

 

 

Задача 13

 

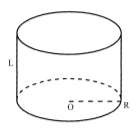Дано:

L= 7см;

С =10 см’ Найти:

S_бок-?  

 

Решение: 1.S_окр=2πrH  или  S_окр= С∙H; 2.    S_бок= 7∙10=70см.

Ответ: 70см.

 

Задача 14

 

Дано: Конус;

BO=12 м;

OO₁ =2 м;

OC=8 м;

 

Найти:

S_окр-?

Решение:

1. Рассмотрим подобные треугольники BOC и BO₁C₁ (по 2-м углам).

;

;

;

12∙O₁С₁ = 8∙20;

12∙O₁C₁ = 80;

O;

;

Ответ: .

 

 

Задача 15 

 

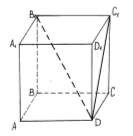Дано: ABCDA1B1C1D1 -  

Прям. Пар-д.;

AB=8 см;

DC=9 см;

 

DC₁=12 см;

Найти: B₁D-?

Решение:

1. B₁D=AB²+BC²+CC₁²;

;

3. B₁D² = 8²+9²+(4√5)²=64+81+80=225; 4. B₁D=15.

Ответ: B₁D=15.

 

Задача 16

 

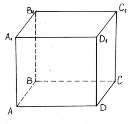Дано:

ABCDA₁B₁C₁D₁        –

правильный параллелепипед;

AB=6 м;  

Стоимость   материала за 6 м² 50 рублей;

Найти:

Сумму            отведенную  на покрытие пола.

 

 

Решение:

 

1.      S_осн=66=36 (м²);

2.      Так как оплата производится за каждые 6 м², найдем количество таких отрезков: 36:6=6; 3. Найдем стоимость: 650=300 рублей.

Ответ: 300 рублей.

 

Задача 17

 

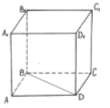Дано:

AB=5 см;

BD=8 см;

AA₁=14 см;

 

Найти:  V-?

Решение:

1. V= a∙b∙c;

   V= AB∙BC∙AA₁;

;

3. V= 5∙ √39 ∙14=70√39.

Ответ: V

 

Задача 18 

 

Дано:

BD=8 см;

H=5 см;

 

Найти: V-?

 

Решение:

 

h;

2  . т.к □ABCD – квадрат найдем его сторону

AD ;

3  .  S_осн (4√2)²=32;

.

Ответ:  

 

Задача 19

 

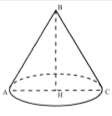Дано:

BH=12 м; HC=8 м;

π=3

 

Найти:

S_бок-?

Решение:

1. S_бок=π∙R²;

;

3.  S_бок=π∙8∙4∙ √13=3∙32√13=96√13 (м²);

4.  96√13*4=384√13/

Ответ: 384√13

 

 

Задача 20

 

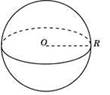Дано: V=32 мм³; π=3;

Найти:  

OR-?

Решение:

;

;

3. 32=4∙OR³;

   ;

OR3=8; OR=2;	Ответ: OR=2.

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ К ОРГАНИЗАЦИИ

УЧЕБНОЙ ДЕЯТЕЛЬНОСТИ ПРИ РЕШЕНИИ ЗАДАЧ

 

 

 

Применяя визуальные модели при решении задач необходимо придерживаться следующим принципам:

-  использование технических средств должно быть обоснованно и не превращаться в самоцель. Применение их признается целесообразным в тех случаях, когда не может быть достигнута педагогическая эффективность при помощи более доступных средств;

-  применение технических средств должно быть системным, а не эпизодическим, так как бесплановое использование их приводит к тому, что насыщаются ими занятия, не нуждающиеся в этом;

-  наглядные изображения обязаны соответствовать логике устного изложения учебного материала, а также соответствовать синхронность рассказа и показа. Разнобой между тем, что аудитория видит, и тем, что она слышит, недопустим, поэтому:

-  важно, чтобы не логика устного выступления подстраивалась под имеющиеся кадры, а, наоборот, кадры подбирались к содержанию выступления и вписывались в логику занятия.

-  ответ на вопрос о том, когда лучше показывать видеофильм (в начале, в конце или середине занятия) становится беспредметным, если руководствоваться методическим требованиям непосредственного сочетания слова и изображения.

 

Комментарий к задаче 1 

Для решения данной задачи целесообразно организовать работу в группах. Каждой группе выдаются предметные визуальные модели: деревянный куб, пластмассовая призма, пирамида из спиц и пр.. Обучающимся, после прочтения текста задачи и обсуждения ее содержания, предстоит выбрать из набора предметов нужную модель. Далее, обсуждаются способы и алгоритмы ее решения, ведется запись в тетрадях. 

 

Комментарий к задаче 2

Учитель предлагает школьником просмотреть видео с изображением спортивного инвентаря боксеров и затем на экране показывает рисунок с геометрическими телами, из которых обучающимся необходимо найти модель, соответствующую содержанию задачи. Далее,  организуя коллективную беседу по решению задачи, учитель предлагает  школьникам заполнить таблицу в процессе обсуждения  наводящих вопросов.

 

Примерные вопросы к беседе:

–               Какие именно данные нам известны из условия задачи и как эти данные соотносятся с элементами выбранной вами модели?

–               Достаточно ли известных данных, для решения задачи? 

–               Какие элементы цилиндра считаются  наиболее характерными?

–               Какие формулы необходимо использовать в решении задачи?

 

Рисунок 3.  Заполненная обучающимися таблица

 

Работа с таблицей, имеющей 5 блоков, является направляющей в выборе учебных действий. Результат заполнения таблицы, предложенной обучающимся, к решению задачи изображен на рисунке 6.

 

Комментарий к задаче 3

Обучающимся предлагается разделиться на группы по 3 человека. Каждой группе раздается задача и её решение. Учитель озвучивает задание: «Постройте чертеж и определите, имеются ли ошибки в решении задачи. Если есть исправьте их и найдите верный ответ».

 

Комментарий к задаче 4

После ознакомления с текстом задачи и просмотра видеофильма о работе мелиораторов, обучающиеся  пытаются определить данные задачи и сопоставить их с данными визуальной модели к задаче. В тетрадях ведется запись в разделе «дано».

То есть обучающиеся составляют алгоритм решения задачи в форме визуальной модели – схемы, изображенной на рисунке 2.

 

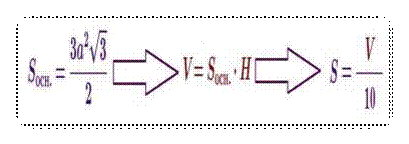
 Рисунок 2. Визуальная модель алгоритма решения задачи 2

 

На следующем этапе обучающимися оформляется решение задачи в тетрадях.

 Далее обучающимся предстоит определить, что для решения задачи необходимо найти объем цистерны, но для этого важно знать площадь цистерны.  

Но чтобы найти площадь цистерны необходимо доказать формулу используя шестиугольник и его свойства.

 

Комментарий к задаче 9

Перед там как обучающиеся приступают к решению данной задачи, учитель представляет объект, указанный в задаче, в виде яркой анимации, а после предлагает выполнить следующее задание к задаче: найти на представленном учителем на доске чертеже лишние элементы, которые мешают решению задачи.

 

 

Комментарий к задачам 11-20

Организуя учебную деятельность обучающихся с использованием анимационных визуальных моделей по решению математических задач:

-  учитель перед началом решения задачи показывает данную фигуру в виде Gif-анимации;

-  обучающиеся перед решением задачи строят чертеж, который отражает в себе сущность увиденной фигуры;

-  сверяют чертеж с фигурой, которую учитель приготовил на следующем слайде;

-  обсуждают алгоритм решения задачи, представляя профессию людей занимающихся решением подобных задач;  записывают решение задачи в тетрадях;

-  делают выводы, обобщения.

 

Визуальные модели к каждой задаче 11-20 представлены на диске, вложенном в учебное пособие.

 

В заключение следует отметить, что в целом методическая работа преподавателя при подготовке к занятиям с техническими средствами включает в себя следующие этапы:

-  ознакомление с информационным фондом и предварительный подбор предположительно необходимых дидактических материалов;

-  просмотр (прослушивание) подобранных материалов и окончательное определение тех, которые подходят к данному занятию;

-  изучение отобранных дидактических материал и продумывание методики использования каждого из них по ходу занятия;

-  разработку общего методического сценария занятия с использованием технических средств обучения.

В процессе обучения решению задач профессионального контекста посредством визуальных моделей автор рекомендует использовать цифровые образовательные ресурсы сети Интернет, например: 

-  https://nsportal.ru/shkola/geometriya/library/2013/05/29/mno gogranniki;

-  https://infourok.ru/prezentaciya-po-matematike-na-temumnogogranniki-klass-915473.html;

-  https://www.youtube.com/channel/UCnooVihOGiBLP20XdW_vBw;

https://www.youtube.com/channel/UC6NEvbUaBx_1GR7IGesCGE

Q;

-  https://www.youtube.com/watch?v=-VWz0tkLJ7c. 

Контроль умений, знаний и навыков обучающихся по теме «Многогранники и тела вращения»  рекомендуется осуществлять при помощи онлайн-тестов, расположенных на сайтах:

-  https://onlinetestpad.com/ru/tests/geometry;  

-  https://otlgdz.com/testy/test-po-geometrii-dlya-9-klassa.html

             

ОТВЕТЫ К ЗАДАЧАМ

 

 

Задача 1: S_AA1D1D=180 м²; количество – 720.

Задача 2: 37.5√3.

Задача 3: 27√3_.

Задача 4: S_бок=28260 см².

Задача 5:.

Задача 6: 376,8.

Задача 7: 753,6 см².

Задача 8: 1 мяч. Задача 9: V₂=960 см³ Задача 10: 120 см².

Задача 11: .

Задача 12: V=336 см³, дозировка=6,72.

Задача 13: 70 см.

Задача 14: .

Задача 15: B₁D=15.

Задача 16: 300 рублей.

Задача 17: V= 70√39.

Задача 18: .

Задача 19: 384√13.

Задача 20: OR=2

             

СПИСОК РЕКОМЕНДОВАННОЙ ЛИТЕРАТУРЫ

 

 

 

1.                 Алексеевская Л. Е. Использование визуальных моделей в процессе обучения математике // Актуальные проблемы обучения информатике в высшей и средней школе: материалы Всероссийской научно-практической конференции /отв. ред. И. В. Ижденева, И. А. Дудковская. - Новосибирск-Куйбышев, КФ НГПУ, Немо-Пресс. - 2017. - С. 178-183.

2.                 Алексеевская Л. Е. Развитие навыков использования визуальных моделей при решении задач профессионального содержания на занятиях по математике // Москва: PORTALUS.RU. Дата обновления: 16 марта 2018. URL: portatalus.ru/modules/different/rus_readme.php?subaction=showfull&id=15

21222956&archive=&start_from=&ucat=&       (дата       обращения:

02.05.2018). 

3.                 Болтянский В. Г. Математическая культура и эстетика // Математика в школе. 2012. № 2. С. 40-43.

4.                 Болтянский В. Г. Формула наглядности – изоморфизм плюс простота // Советская педагогика. 2008. № 5. С. 46-60.

5.                 Далингер В. А. Геометрия помогает алгебре // Математика в школе. 2008. № 4. С. 29-34.

6.                 Далингер В. А. Когнитивно-визуальный подход // Методика обучения математике. 2016. 33 с.

7.                 Штофф В. А. Моделирование и философия. Москва :

Наука, 1966. 302 с.

             

ДИСК С ПРЕЗЕНТАЦИЯМИ

          

Учебное издание

 

 

Алексеевская Любовь Евгеньевна

 

РЕШАЙ ВИЗУАЛИЗИРУЯ 

И ВЫБИРАЙ ПРОФЕССИЮ 

НА УРОКАХ МАТЕМАТИКИ

 

(Оригинал-макет учебного пособия)

 

 

 

 

______________________________________

 

ОРИГИНАЛ-МАКЕТ