Решение  экономических задач ЕГЭ.

Канаткалиева М.Э., учитель математики МАОУ «СОШ№23 им.Г.А.Кадзова» Приближается пора сдачи экзаменов. В помощь ученикам 11 класса хочу предложить примеры решения, так называемых, банковских задач. Предлагаю один из способов решения.

31 декабря 2013 года Сергей взял в банке 9930000 рублей в кредит под 10% годовых. Схема выплаты кредита, следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Сергей переводит в банк определенную сумму ежегодного платежа. Какой должна быть сумма ежегодного платежа, чтобы Сергей выплатил долг тремя равными ежегодными платежами? S= 9930000 руб. r = 10%

𝑟𝑟

          к =1+        ;    к=1+  = 1+0,1=1,1- коэффициент увеличения

₁₀₀

Х - сумма ежегодного  платежа

                                     kS                       k(kS − X) = k2S − kX                k(k2S − kX − X) = k3S − k2X − kX

 Долг

                                     Остатокдолга  kS−X                    k2S − kX − X                          k3S −k2X −kX − X = 0

k³S−k²X −kX −X = 0  k³X +kX +X =k³S                  

X(k³ +k+1) =k³S                                              Х

X = k2 k3kS³S+(1k−1) k³S(k−1)         Х = 1331331⋅993000 =1331⋅3000 = 3993000. +

X = (k2 k+k₊1)(k₋1) = k3 ₋1            

Проверка:

Ответ: 3993000 руб.

Задача №2

В июле планируется взять кредит в банке на сумму 10 млн рублей на 5 лет. 

Условия его возврата таковы:  

-каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;  

-   с февраля по июнь каждого года необходимо выплатить часть долга;  

-   в июле каждого года долг должен быть на одну и ту же величину меньше долга  на июль предыдущего года. Сколько млн рублей составила общая сумма выплат после погашения кредита?  

S=10 млн. руб. r = 10%

𝑟𝑟

          к =1+        ;    к=1+  = 1+0,1=1,1- коэффициент увеличения

₁₀₀

n=5лет

В июле каждого года долг должен быть на одну и ту же величину меньше долга  на июль предыдущего года,  поэтому  кредит ежегодно уменьшается на 2 млн. рублей  

(10 млн :5=2 млн)

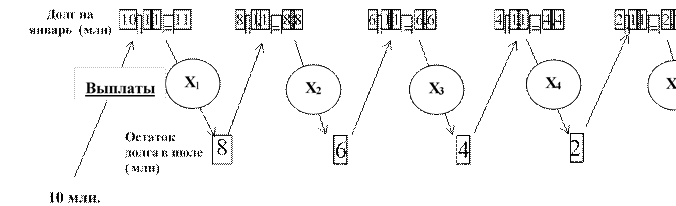
Х1 = 11- 8= 3 млн.  

Х2 = 8,8-6= 2,8 млн.  

Х3= 6,6- 4=2,6  млн.  

Х4= 4,4- 2= 2,4 млн.  

Х5= 2,2 млн.  Находим общую сумму выплат: 3+2,8+2,6+ 2,4+2,2= 13млн. Ответ: 13 млн. рублей.

Выводы: 

•      наибольшая  выплата – первая;

•      наименьшая  выплата – последняя;

•      долг  на январь, выплаты и остаток долга  образуют арифметическую прогрессию;

•      n-й член арифметической прогрессии будет равен a_n = a₁ + (n −1)d ;

•      сумма первых n членов арифметической прогрессии равна S_n .

Задача №3

В июле планируется взять кредит в банке на сумму 8 млн рублей на некоторый срок. Условия возврата таковы:  

•      -каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;  

•      -с февраля по июнь каждого года необходимо выплатить часть долга;  

•      -в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.  

На какой минимальный срок следует брать кредит, чтобы наибольший годовой платёж по кредиту не превысил 3,6 млн руб.?  S=8 млн. руб. r = 25%

𝑟𝑟

к =1+ 100;    _к- коэффициент увеличения

Хнаибольший ≤ 3,6млн.

n=? - минимальный срок кредита

В июле каждого года долг должен быть на одну и ту же величину меньше долга  на июль предыдущего года,  поэтому  кредит ежегодно уменьшается на ^𝐒𝐒 млн. рублей, т.е. на

𝐧𝐧 𝟖𝟖  млн. руб.

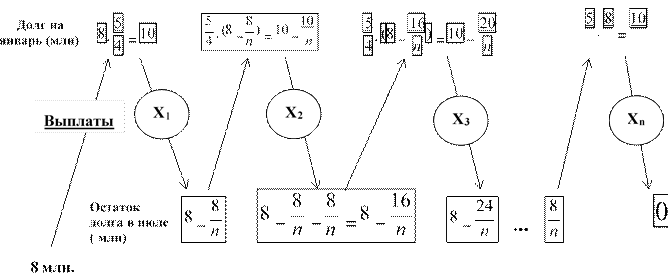𝐧𝐧

                                                                                                                                                   4 n       n

Наибольшая выплата – первая: Х

По условию задачи наибольший годовой платёж  ≤  3,6 млн. руб.

           Х1 = 2+ 8n≤3,6                                            8−1,6n≤ 0

8 ≤1,6                 −n1≥,68n:1≤,6−8 n

8−n1,6n≤ 0 n≥ 5 n> 0, значит 8-1,6n ≤ 0

Ответ: 5.