Решение неравенств методом интервалов.

Решение неравенств методом интервалов.

Метод интервалов это универсальный метод решения неравенств. Он подходит для решения разнообразных неравенств, однако наиболее удобен для решения рациональных неравенств с одной переменной. Знакомство с методом интервалов начинается при решении неравенств вида f(х). Конечно знак неравенства может быть любым: <; ≥; ≤»). Где f(х) либо многочлен, представленный в виде произведения линейных двучленов с коэффициентом 1при переменной или квадратных трехчленов со старшим коэффициентом 1с отрицательным дискриминантом и их степеней, либо отношение таких многочленов. Например

1.(х-7)(х+7)

2. 

3.

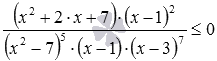
Рассмотрим функцию f(х)= (х+2)(х-3)(х-5).

Областью определения этой функции есть множество всех действительных чисел. Функция обращается в нуль при х= -2, х=3, х=5.  (Эти значения называются нулями функции).  Они разбивают область определения на промежутки:  (-∞; -2), (-2; 3), (3; 5) и (5; +∞).  Выясним какой знак принимает функция f(х) = (х+2)(х-3)(х-5) в каждом из этих на этих промежутков.             Выражение  (х+2)(х-3)(х-5) представляет собой произведение трех множителей. Множитель (х+2) отрицателен при  х < -2 и положителен при  х> -2,   множитель (х-3) отрицателен при  х<3  и положителен при  х >3,  множитель  (х-5)  отрицателен при х<5 и положителен при х>5. Знаки каждого из рассмотренных  промежутков удобнее заносить в таблицу. В этом случае   ученикам  наглядно видно какой знак будет иметь  искомая функция f(х)= (х+2)(х-3)(х-5) на всей области определения.

Отсюда видно, что f(х) <0, если х€ (-∞; -2), т.к. каждый из рассмотренных множителей на этом промежутке принимает отрицательное значение. Произведение трех отрицательных чисел – величина отрицательная. 

Если х€(-2; 3), то f(х) >0.  (первый множитель положителен, второй и третий отрицательны.

Если х€(3; 5), то f(х) <0 ( первый и второй множители положительны, а третий отрицательный).

Если х€(5; +∞), то f(х) >0.( Все три множителя положительны). Мы видим, что в каждом из промежутков (-∞; -2), (-2; 3), (3; 5) и (5; +∞) функция сохраняет свой знак и при переходе через точки -2; 3 и 5 ее знак меняется.

Вообще если функция задана формулой вида f(х)= (х-х1)(х-х2)…(х-хn ) гдех – переменная, а х1, х2, х3… не равные друг другу числа, то в каждом из промежутков, определенных нулями функции , эта функция сохраняет знак , а при переходе через нули функции ее знак меняется.

Использование  метода интервалов целесообразно использовать при решении неравенств вида: (х-х1)(х-х2)(х-х3)…(х-хn)  ≥ 0.     (1) При   этом следует обратить внимание на то , что х1,х2, х3, … хn – не равные друг другу числа.

Пример1. Решить неравенство (х+6)(х+1)(х-4)

Для решения неравенства выполним следующие шаги:

1.      Выясним является ли наше неравенство неравенством вида (1) – да является.

2.      Найдем нули функции f(х)= (х+6)(х+1)(х-4). Это числа -6; -1; 4.

3.      Расположим данные числа на числовой прямой и получим промежутки (-∞;-6) ; (-6; -1); (-1; 4); (4;+∞).

4.      Найдем знаки функции f(х)= (х+6)(х+1)(х-4) в каждом из указанных промежутков. Для этого достаточно найти знак в одном из них, и пользуясь свойством знакочередования , определить знаки в остальных промежутках. При этом удобно начинать с крайнего справа промежутка  (4;+∞),  так как в нем значение функции f(х)= (х+6)(х+1)(х-4)  заведомо положительно. Знаки функции на остальных промежутках будут соответственно:

      -     -6             +             -1            -            4                     +                   х

      5.Выбираем значения х удовлетворяющие условию задания. Это объединение промежутков: (-∞;-6) и (-1; 4).

Пример 2.

Решить неравенство    (х² -9)(х+1,5)>0.

Обращаем внимание на то, что данное неравенство отличается от неравенства(1). Для того чтобы воспользоваться описанным выше методом интервалов разложим двучлен х² -9 на множители (х-3)(х+3). Исходное неравенство принимает вид (х-3)(х+3)(х+1,5)>0.  Это неравенство вида(1). Поэтому можно воспользоваться методом интервалов. Отметим на числовой прямой нули функции f(х)= (х-3)(х+3)(х+1,5)   3; -3; -1,5.

При х>1,5 f(х) >0. Далее при перемещении влево по прямой используем знакочередование при переходе через нули функции.

              -         -3        +        -1,5              -             3                       +                        х

Ответ: (-3; -1,5); (3; +∞).

Рассмотрим применение данного метода к решению различного вида:

Пример 3.

Решить неравенство:     (5х+1)(5-х)>0

Решение:

Вынесем за скобки множитель 5 в первом двучлене и множитель -1 во втором. Получим неравенство -5(х+1/5)(х-5) >0; (х+1/5)(х-5) <0

(х+1/5)(х-5) >0 (х+1/5)(х-5) принимает значения равные нулю при х=-1/5 и х=5.

f(х)>0 при х€(-∞; -1/5);(5;+∞);     f(х)<0 при х€ (-1/5; 5)

Ответ:  (-1/5; 5).

Пример  4.

Решить неравенство:     (х⁴+8)(4-х)(х+1/3) ≤ 0.

Решение:

В произведение  (х⁴+8)(4-х)(х+1/3) входит множитель  (х⁴+8), который принимает значения больше нуля при любом значении х. Поэтому исходное неравенство равносильно неравенству   (4-х)(х+1/3) ≤ 0. Последнее неравенство приведем к виду

-(х-4)(х+1/3) ≤ 0

(х-4)(х+1/3) ≥ 0

Нули функции х=4 и х=-1/3

f(х)>0 при х € (-∞; -1/3); (4;+∞)

f(х)<0 при х € (-1/3;4)

Ответ: (-∞; -1/3); (4;+∞).

Пример 5.

Решить неравенство:     (х+8)(х-1)⁶(х-5) < 0.

Решение:

В произведении  (х+8)(х-1)⁶(х-5) множитель  (х-1)⁶ >0 при любом х кроме х=1. Поэтому при всех значениях х≠1 произведение  (х+8)(х-1)⁶(х-5) имеет тот же знак , что и произведение (х+8)(х-5).

Решение неравенства  (х+8)(х-1)⁶(х-5) < 0 равносильно решению системы

{(х+8)(х-5)<0, х≠1.

Применим к неравенству (х+8)(х-5)<0 метод интервалов находим множество его решений (-8;5). Чтобы найти все решения искомого неравенства

(х+8)(х-1)⁶(х-5) < 0 нужно из полученного промежутка (-8;5) исключить число 1. Получаем решение заданного неравенства (-8;1);(1; 5).

Ответ:  (-8;1);(1; 5).

Пример 6.

Решить неравенство:   

>0  (1)

Решение :

Данное неравенство равносильно неравенству  (х-7)(х+2)>0,т.к. дробь (1) положительна только при тех значениях х, при которых оба двучлена х-7 и х+2 имеют одинаковые знаки. Но при этих же условиях положительно и произведение этих двучленов. А следовательно для решения неравенства     (х-7)(х+2)>0 удобно воспользоваться методом интервалов.

Нулями функции f(х)= (х-7)(х+2)>0 являются числа 7 и -2.

              +            -2                        -                   7                                   +                                    х

Решением неравенства  (х-7)(х+2)>0 является множество (-∞;- 2); (7; +∞)          А следовательно и решением неравенства (1) являются эти же промежутки.

Ответ: (-∞;- 2); (7; +∞).

Пример  7.

Решите неравенство:     ≤0     (1)

Решение:

Следует отметить, что в данном случае невозможно воспользоваться предыдущим приемом, т.к.     неравенство  (1) и неравенство (х+4)(х-11)≤0 не равносильны. Число является 11 решением  неравенства (2), но  не является решением неравенства (1). При х=1 неравенство (1) не имеет смысла. Поэтому чтобы решить неравенство (1) заменим его равносильной системой

Решением неравенства  (х+4)(х-11)≤0 есть промежуток   [-4; 11]. Т.к х≠ 11, получаем  [-4; 11).

Ответ: [-4; 11).

 Стоит обратить внимание на то, что в подавляющем большинстве случаев при решении рациональных неравенств их предварительно приходится преобразовывать к нужному виду, чтобы стало возможным решение методом интервалов.

Подход, лежащий в основе метода интервалов . имеет место в силу следующего свойства непрерывной функции: если на интервале (а;в) функция f(х) непрерывна и не обращается в нуль, то она на этом сохраняет постоянный знак. А это свойство в сою очередь следует из теоремы Больцано –Коши (ее доказательство не рассматривается в школьном курсе математики, но с учениками проявляющими повышенный интерес к предмету математика ее доказательство можно рассмотреть в книге Курс математического анализа (в двух томах), учебник для студентов университетов и втузов.

Сформированные  у обучающихся прочные навыки    решения неравенств с помощью данного метода позволит им решать и другие задачи, решение которых сводится к решению неравенств.

Например найти область определения функции    у=.

Решение:

Необходимое условие существования квадратного корня , чтобы выражение      х(х+9)(2х-8)≥0.

 2х(х+9)(х- 4)≥0

х(х+9)(х- 4)≥0

           -           -9                  +               0            -         4                     +                х              

Ответ:  [-9; 0]; [4; +∞).

Итак   метод интервалов позволяет решать неравенства вида f(x)<0 (≤, >, ≥), где f(x) – произвольное выражение с одной переменной x.  И еще раз напомним алгоритм решения неравенств обобщенным методом интервалов:

·         Сначала надо найти область определения функции f и нули этой функции.

·         После этого граничные точки области определения и нули функции переносятся на числовую прямую, причем нули функции изображаются выколотыми точками при решении строгих неравенств (возможны случаи, когда они будут совпадать с граничными точками области определения, эти точки делают выколотыми), а при решении нестрогих неравенств – обыкновенными точками. Нули разбивают область определения функции на промежутки.

·         Дальше определяются знаки на каждом промежутке области определения, в основном путем вычисления значения функции f в какой-либо одной точке из каждого промежутка.

·         Если решается неравенство со знаком < или ≤, то наносится штриховка над промежутками со знаком −, а если решается неравенство со знаком > или ≥, то над промежутками со знаком +. И по полученному изображению числового множества записывается ответ.

Список литературы:

1.Алгебра. 8 класс. В 2 ч. Учебник для учащихся общеобразовательных учреждений /А.Г. Мордкович- 11 изд., стер. – М.: Мнемозина, 2009.215с. ISBN 978-5-346-01155-2

2. Алгебра. 9 класс. В 2 ч. Учебник для учащихся общеобразовательных учреждений /А.Г. Мордкович, П.В. Семенов. - 10 изд., перераб. – М.: Мнемозина, 2008.  224 с. ISBN 978 -5-346-00990-0

3.Алгебра. 9 класс. В 2 ч. Учебник для учащихся общеобразовательных учреждений / Ю.Н. Макарычев, Н.Г. Миндюк,   К.И. Нешков/ под ред. С.А. Теляковского. 16-е изд. М. Просвещение, 2009.- 271с.:ил.- ISBN978-5-090021134-5.

4  .Алгебра. 9 класс. В 2 ч. Учебник для учащихся общеобразовательных учреждений /  А.Г. Мордкович, П.В. Семенов 13-е изд. М. Мнемозина , 2011.- 222с.:ил.- ISBN978-5-346-01752-3. 

5.Алгебра и начала анализа Учебник для 10 и 11 классов общеобразовательных учреждений /А.Н.

Колмогоров, А.М. Абрамов, Ю.П. Дудницин и др.; Под ред. А.Н. Колмогорова.-14 изд.- М., Просвещение, 2004.- 384с.: ил. ISBN 5-09-013651-3

5.      Кудрявцев Л.Д. Курс математического анализа ( в двух томах): Учебник для студентов университетов и втузов. – М. Высш. Школа, 1981.

Скачано с www.znanio.ru