Решение показательных уравнений

Конспект урока алгебры и начала анализа в 11 классе

 по теме «Решение показательных уравнений».

Цели урока:

1.      Повторить, обобщить и систематизировать теоретические знания и методы решения показательных уравнений и их систем.

2.      Подготовиться к проверочной работе по изученной теме.

Ход урока:

I. Организационный момент.

    Ребята, на протяжении ряда уроков мы решали показательные уравнения. Сегодня на двух уроках мы вспомним все способы решения показательных уравнений и подготовимся к проверочной работе, которая будет на следующем уроке.(слайд №1)

Вопросы к классу:

·        Какие уравнения называются показательными?

·        Какие способы решения показательных уравнений мы знаем?

а)приведение степеней в левой и правой частях уравнения к одному основанию;

б)разложение  частей  уравнения на множители;

в)введение новой переменной;

г)графический способ решения;

д)деление на степень;

е)оценивание значения левой и правой частей уравнения с помощью свойств показательной функции, подбор корня.

II. Устная работа:

                                     Слайд №2:

Ответы к уравнениям:

1.  х=3

2.  х=3

3.  х=0

4.  х=-2

Слайд №3:

5.  х=-2

6.  х=-3

7.  х=-2,5

8.  х=4

                                       Слайд №4:

9.  х= 8

10 . х=5,5

11. х=-2,

 12. х=3

 

III. Решение упражнений:

Слайд №5:

(Первое уравнение решаем всем классом на доске, а второе и третье уравнения по вариантам – два  ученика работают у доски) 

1.()^х+2=()⁶                                       2х=10       

   -2(х+2)=6                               х=-5  

                                                       3. (  )^х+1-( )=0 

                                                             -2(х+1)=1

2. ()^5х-4=                                        -2х-2=1

     2(5х-4)=-3                                        -2х=1

     10х-8=-3                                                                                    х=-0,5

     10х=5                   

      х=0,5

 Слайд №6:

(Два первых уравнения решаем всем классом на доске, а остальные - по вариантам – два  ученика работают у доски. Взаимоконтроль.) 

 

1.   8^х+2-32^х=0                                    3. 25^х+3=125^х

      3(х+2)=5х                                        2(х+3)=3х

      3х+6=5х                                           2х+6=3х

      -2х=-6                                               -х=-6

       х=3                                                    х=6

 

2. 9^х-5-27^х=0                                    4. 49^2х+3-343^х=0

   2(х-5)=3х                                          2(2х+3)=7х

   2х-10=3х                                           4х+6=7х

   -х=10                                                 -3х=-6

   х=-10                                                   х=2

 

    Слайд №7: (Первое уравнение решаем всем классом на доске, а второе и третье уравнения по вариантам – два  ученика работают у доски) .

1.  ( )^3-2,5х=8^х-1/3                          2. ()^5-2х=4^х-3

      -2(3-2,5х)=3(х-1/3)                    -3(5-2х)=2(х-3)

      -6+5х=3х-1                                 -15+6х=2х-3

      2х=5                                                  4х=12

      х=2,5                                                  х=3

 

     3. )^3-2х=16^х-1/2

    -3(3-2х)=4(х-1/2)

     -9+6х=4х-2

      2х=7

      х=3,5

 

Слайд №8: (Первое уравнение решаем всем классом на доске, а второе и третье уравнения по вариантам – два  ученика работают у доски) 

1. 64·8^1+2х=16^2+х               2. 4:16^1-2х=8^2+х

     8+3(1+2х)=4(2+х)       2-4(1-х)=3(2+х)

     8+3+6х=8+4х               2-4+4х=6+3х

     2х=-3                             х=8

     х=-1,5

 

3. 128·4^1-2х=8^2-х                            

     7+2(1-2х)=3(2-х)                   -х= -3

     7+2-4х=6-3х                          х=3

Слайд №9:

1. ₂·₂^х=₂₅₆       2.₄: ₄^х=₆₄  

+х=8                          - х=3

х²-16=8-х                               =3+х

х²-16=64-16х+ х²                     6х+58=9+6х+х²

16х=48                                   х²=49

х=3                                         х=±7(выполнить проверку)

 

3.

        +2х=3

           5х²-9х-1=9-12х+4х²

           х²+3х-10=0                                         

           х=-5, х=2(выполнить проверку)

 

Слайд №10:

1. 2^х+5-2^х=62           2.

    2^х(32-1)=62              2^х+4(20+3)=23

    2^х=2                          2^х+4=1

    х=1                            х+4=0

                                       х=-4

 

Слайд №11:

1.9^х-4·3^х-45=0                                    2. 4^{sin х}+2^{1+sin х}-8=0

   Пусть 3^х=t, t›0                                    Пусть 2^{sin х}= t, t›0 

   t²-4 t-45=0                                            t²+2 t-8=0

  Д=16+4·45=196                                   t₁=-4, -4<0

  t₁₌=-5,-5<0                                    t₂=2

  t₂=9                                                       2^{sin х}=2

  3^х=9                                                      sin х = 1

  х=2                                                       х=+2πк,к Є Z

 

 

 

Слайд №12(первое уравнение – сильный ученик у доски, второе уравнение – самостоятельно – один ученик на переносной доске)

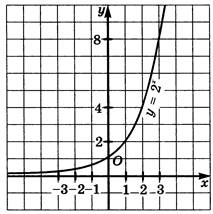
1.2^х=6-х

  х=2

 

 

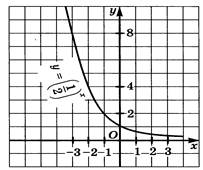
2.     ( ½)^х=х+6                                      

        х=-2

 

 

 

 

 

 

 

                                                      

                                                                    Слайд №13(первое уравнение – сильный ученик у доски, второе уравнение – самостоятельно, предварительно обговорив ход решения, – один ученик на переносной доске)

    

                                                                1. 2^2х+1 - 7·10^х + 5^2х+1=0

                                                                   2^2х·2- 7·2^х · 5^х +5^2х·5=0  (: 5^2х≠0)

                                                                   2·()^2х-7 ()^х+5=0

                                                                 Пусть     ( )^х= t, t›0

                                                                  2 t²-7 t+5=0

                                                                  Д=49-4·2·5=9

                                                                  t₁==1,   t₂=

                                                              ()^х=1       ()^х=      

                                                               х = 0          х=-1                                 

2.  2·9^х - 6^х=3·4^х

    2·3^2х - 2^х·3^х - 3·2^2х=0 ( : 2^2х≠0)

    2·(1,5)^2х-(1,5)^х-3=0

    Пусть (1,5)^х= t, t›0

     2 t²- t-3 = 0

    Д=1+4·2·3=25

   t₁== - 1, -1<0,       t₂=

    (1,5)^х=1,5

     х=1

                                                  Слайд№14: (Первую систему уравнений решаем всем классом на доске, а вторую и третью - по вариантам – два  ученика работают у доски) 

1. 6^3х:6^у=√6,    3х-у=½,   

    2^у:2^2х=;     у-2х=-½;                  

                         х= 0,        

                          у=-½.

 

                                        Ответ: (0,-½)

2. 0,5^3х·0,5^у=0,5,   3х+у=1,                   х=1,

    2^3х·2^-у=32;         3х-у=5;                    у=-2.

                                                                6х=6

                                                                  х=1

                                            Ответ: (1,-2)

 

 

3. (√5)^2х+у=(√)√5,    2х+у=0,                   х=-1,              

     ()^х·5^у=125;            -х+у=3;                   у=2.     

                                      3х=-3

                                       х=-1

                                                                                                           Ответ: (-1,2)

IV. Рефлексия. С каждого урока ученик должен унести хоть что-то новое: знание, умение, навык. Что вам дал сегодняшний урок?

 Выставление оценок за урок.

V. Домашнее задание.