Решение полного уравнения четвертой  степени.

( способ Феррари)  [1] Рассмотрим полное уравнение четвертой степени вида:

x⁴  sx³  px²  qx  r  0 .                                (3.1) Перенесем три последние члены уравнения (3.1) в правую часть и

s2 x2 прибавим к обеим частям,         , что дает нам возможность левую часть

4

уравнения превратить в полный квадрат:

                           2          s   2        s2               2

                   x  2 x  _ ₄  p_x  qx  r .                                                               (3.2)

Прибавим к обеим частям уравнения (3.2) сумму x2  s xy y2 ,

                                                                                                                                                                               2             4

уравнение принимает вид:

                             ₂         s    y ²       s²                           ₂       s                y²          

                        x       4  p  yx  2  y qx  4 r.      (3.3)

                                        2    2     

Подберем вспомогательное неизвестное y таким образом, чтобы правая часть уравнения (3.3) тоже превратилась в полный квадрат, это будет, очевидно в том случае, когда:

                          s2                                  2 s                        y2                            2

 4  p y A , 2 yq  2AB, 4 r  B . 

Но 4A²B² 2AB² , поэтому должно быть:

                            s ²                      y ²             s        ²

4 4  p  y 4  r   2 y  q .

Раскрыв, скобки и произведя преобразования, получим уравнение третьей степени относительно вспомогательного неизвестного (y) :

                     y³  py ²  ysq  4rr(s²  4p)  q ²  0.                                         

(3.4)

Пусть    y₀ какой-нибудь действительный корень этого уравнения, подставляя его в уравнение (3.2), мы превратим его правую часть в полный квадрат Ax  B² :

2

                                     ₂          s       y₀     AxB²,

                                      x  x        

                                           2        2 

                                          2          s        y0

x  2 x  2  Ax  B

            отсюда:                                         ,                                                                 

x2  s x  y0  Ax  B

                                      ^      2        2

(3.5)             где      A 

                                                              sy⁰                                                                              sy⁰

             1,         если q  0,1, если q 0. 

                                                                2                                         2

Эти два квадратных уравнения и дадут нам все четыре корня уравнения

(3.1).

Таким образом, доказано, что решение уравнения четвертой степени сводится к решению уравнения третьей степени (3.4) и двух уравнений второй степени (3.5). 

 Решение полного уравнения четвертой степени методом Феррари.

(Вывод автора)

        Решение Л. Феррари может быть получено без введения каких-либо искусственных преобразований, чисто алгебраическим путем.

Рассмотрим полное уравнение 4 степени вида (3.1) x⁴  sx³  px²  qx  r  0 . 

Уравнение (3.1), как рассматривалось выше, может быть разложено на два квадратных уравнения, т. е.:

x⁴  sx³  px²  qx  r x² x  _x² x _.                              (3.6)

Перемножим квадратные трехчлены и произведем преобразования, в результате получим следующее уравнение: x⁴  x³  x²  x  0.                                                    

(3.7)

Уравнение (3.7) эквивалентно уравнению (3.1), следовательно, мы можем составить следующую систему уравнений:

  s



  p

                                       2               2               2              2

Подставим вновь полученные значения коэффициентов квадратных трехчленов уравнения (3.7), в систему уравнений (3.8):

                               s2  z2

                         _y   p

                                    4

 y t  s  z   s  z  y t 

                                                  q                                                  (3.11)

_ 2  2   2  2 

y2 t2

                           r .

                              4

Произведем алгебраические преобразования во втором уравнении системы (3.11), в результате получим более простую систему уравнений:

                              s2  z2

                        _y   p

                               4

                       sy  zt  2q     ,                                                                           (3.12)

                          2            2

y t  4r





4y  s²  z² 4p



                         sy  zt 2q          ,                                                                        (3.13)

                            2            2

_y t 4r

z² 4y  s² 4p



                        zt  sy 2q         .                                                                      (3.14)

                            2            2

_y t 4r

Выразим из первого уравнения системы (3.14) переменную (z) , из второго уравнения переменную (t) и подставим в третье уравнение системы (3.14):

z ²  4y  4p  s ² ,                                 (3.15) z_1,2,                                  (3.16)

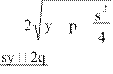                          t               ,                                                                                  (3.17)

z

² sy 2q²

                           y    4r .                                                                     (3.18)

                                         z     

Подставим значение переменной (z ² ) из (3.15) в (3.18):

                              2        sy 2q²

                           y  ₂  4r .                                                               (3.19)

4y 4ps

Произведя преобразования в (3.19) получим окончательно следующее уравнение: y³  py ²  yqs  4r r4p  s ²  q²  0.                               (3.20) Данное уравнение полностью совпадает с уравнением (3.4).

Пусть y₀ - действительный корень уравнения (3.20), тогда значения остальных неизвестных переменных (z) и (t) могут быть найдены из выражений (3.16) и третьего уравнения системы (3.14).

z1,2  2

                                                                                                                                               (3.21)

t1,2

После того, как найдены значения переменных (z) и (t) , необходимо разобраться со знаками перед радикалами в выражениях (3.21).

Для этого введем величину , определяющую знак перед радикалами выражений (3.21).

Если принять, что найденное значение (z_1,2 ) имеет только один знак  (+), тогда знак перед значением (t_1,2 ) может быть определен только из второго уравнения системы (3.12):

sy  2q  zt .

Если sy  2q  0, то (t) должно иметь знак (+), если sy  2q  0, то (t) должно иметь знак (-), поэтому, введя величину , мы можем написать следующее условие:

1, если sy₀  2q  0,

         1, если sy₀  2q  0.      

После определения знаков перед найденными значениями (z_1,2 ) и (t_1,2 ) мы можем найти значения коэффициентов квадратных трехчленов уравнения (3.6) из выражений (3.10):

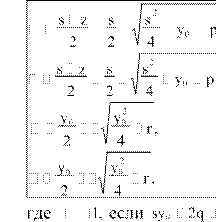                                                    (3.22)

                                1, если sy₀  2q  0.         

Таким образом, решение уравнения четвертой степени (3.1) сводится к решению полного кубического уравнения (3.20) и к решению двух квадратных уравнений:

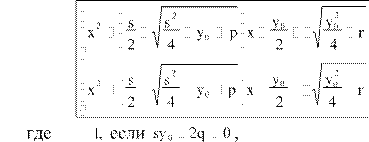                                 (3.23)       1, если sy₀  2q  0.