Контрольная работа 

по учебной дисциплине ЕН.01 «Математика»

1 задание. Решить систему уравнений методом Крамера.

5𝑥 − 2𝑦 + 4𝑧 = 13

1.{ 7𝑥 + 6𝑦 − 2𝑧 = 13

−3𝑥 + 2𝑦 + 7𝑧 = 22

11𝑥 − 3𝑦 + 6𝑧 = 23

2.{ 2𝑥 + 9𝑦 − 5𝑧 = 5

−6𝑥 + 8𝑦 + 4𝑧 = 22

7𝑥 − 4𝑦 + 3𝑧 = 11

3.{ 5𝑥 + 6𝑦 − 8𝑧 = 9

−2𝑥 + 3𝑦 + 7𝑧 = 25

3𝑥 − 5𝑦 + 8𝑧 = 17

4.{−7𝑥 + 4𝑦 + 8𝑧 = 25

6𝑥 + 2𝑦 − 3𝑧 = 1

2𝑥 − 10𝑦 + 7 = 3

5.{ 6𝑥 − 7𝑦 + 9𝑧 = 10

−3𝑥 + 5𝑦 + 8𝑧 = 31

7𝑥 − 2𝑦 + 4𝑧 = 15

6.{ 6𝑥 + 8𝑦 − 7𝑧 = 1

−5𝑥 + 8𝑦 + 3𝑧 = 20

2𝑥 − 7𝑦 + 8𝑧 = 12

7.{−4𝑥 + 7𝑦 + 2𝑧 = 16

8𝑥 + 6𝑦 − 5𝑧 = 5

5𝑥 − 2𝑦 + 3𝑧 = 10

8.{6𝑥 + 8𝑦 − 2𝑧 = 16

−7𝑥 + 4𝑦 + 2𝑧 = 7

8𝑥 + 10𝑦_7𝑧 = 7

9.{ 4𝑥 − 8𝑦 + 6𝑧 = 6

−7𝑥 + 5𝑦 + 2𝑧 = 9

9𝑥 + 5𝑦 − 2𝑧 = 13

10{ 5𝑥 − 6𝑦 − 2𝑧 = 13

−3𝑥 + 8𝑦 + 5𝑧 = 28

2 задание.Вычислите определенный интеграл по формуле Ньютона-Лейбница

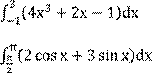1.

2.

3.

2                          ² − 1)dx.

4∫₁ (2x − x

3                          ³ + x² + 7)dx

5.∫₋₁(4x

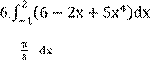
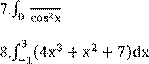
9.∫₋⁵₂(2x − 3x² + 4)dx

10.∫₀¹(1 − x² + x³)dx

3  задание. Применение интеграла.

1.       Скорость движения тела задана уравнением v = 6t + 4 м/с. Найдите путь за две секунды от начала движения.

2.       . Скорость движения тела задана уравнением v(t) = 15 − 3t м/с. Какой путь пройдет тело за 5 секунд от начала движения?

3.       Скорость прямолинейного движения точки изменяется по закону v(t) = 3t² − 12t + 6. Найдите функцию, выражающую путь, пройденный точкой.

4.       Найдите путь, пройденный точкой за первые 5сек от начала движения, если скорость точки меняется по закону v(t) = 10 − 2t м/с

5.       Запишите в виде определенного интеграла площадь фигуры, ограниченной линиями y = x, x = 2, x = 3, y = 0 и вычислите ее площадь.

6.       Запишите в виде определенного интеграла площадь фигуры, ограниченной линиями y = x² + 1, x = 1, x = 2, y = 0 и вычислите ее.

7.       Запишите в виде определенного интеграла площадь фигуры, ограниченной линиями y = x² + 2, x = 1, x = 2, y = 0 и вычислите ее.

8.       Запишите в виде определённого интеграла площадь фигуры, ограниченной линиями, и вычислите ее:  

9.       Запишите в виде определенного интеграла площадь фигуры, ограниченной линиями y = x, x = 2, x = 3, y = 0 и вычислите ее площадь.

10.   Запишите в виде определенного интеграла площадь фигуры, ограниченной линиями y = 5 − 3x², x = −1, x = 1, y = 0 и вычислите ее.

4  задание. Исследование функции с помощью производной.

1.      Исследовать функцию на монотонность и экстремумы: f(x) = x³ − 6x² + 9x − 3

2.      Исследовать функцию на монотонность и экстремумы f(x) = x³ − 3x² − 24x + 6

3.      Исследуйте функцию на возрастание, убывание и экстремумы f(x) = x³ + 6x² + 9x + 8

4.      Исследуйте функцию на возрастание, убывание и экстремумы f(x) = 2x³ − 6x² − 18x + 5

5.      Исследуйте функцию на монотонность и экстремумы f(x) = 2x³ − 3x² − 36x + 6

6.      Исследовать функцию на монотонность и экстремумы f(x) = 4x³ − 27x² + 24x − 3

7.      Исследовать функцию на монотонность и экстремумы f(x) = −2x³ + 10x² − 6x + 1

8.      Исследовать функцию на монотонность и экстремумы f(x) = 2x³ − 3x² − 120x + 1

9.      Исследовать функцию на монотонность и экстремумы f(x) = 2x³ − 3x² − 36x + 5

10.  Исследовать функцию на монотонность и экстремумы f(x) = −x³ + 3x² + 45x − 1

5  задание.Записать уравнение касательной и нормали к графику функции

//y=A𝑥² − 𝐵𝑥 + 𝐶( А- номер варианта, В -день Вашего рождения, С- номер дома, в котором Вы живете)

В точке х₀= -2

6  задание . Решение квадратных уравнений с комплексными корнями.

1.      𝑥²-4х-13=0

2.      𝑥² − 14х + 113 = 0

3.      𝑥² − 2х + 101 = 0

4.      𝑥²-6х+13=0

5.      𝑥² − 10х + 26 = 0

6.      𝑥² − 6х + 25 = 0

7.      𝑥²-4х+29=0

8.      𝑥² − 14х + 50 = 0

9.      𝑥² − 8х + 25 = 0

10.  𝑥² − 4х + 40 = 0

7  задание. Найти сумму, разность, произведение и частного двух комплексных чисел.

1.      𝑧₁= 3+2i         𝑧₂=4-3i 2. 𝑧₁= 5-3i         𝑧₂=2+6i 3. 𝑧₁=  5-4i        𝑧₂=2+5i 4. 𝑧₁=  2-3i        𝑧₂=4+5i 5. 𝑧₁= 3-6i         𝑧₂=1+8i 6. 𝑧₁=7-3i          𝑧₂=2+2i

7.      𝑧₁=1+6i          𝑧₂=5-2i

8.      𝑧₁=4-6i          𝑧₂=3+4i 9. 𝑧₁=3-9i          𝑧₂=5+2i

10. 𝑧₁=7+2i          𝑧₂=2-5i

8  задание. Скалярное произведение векторов

1.      Найдите скалярное произведение векторов ⃗a  и ⃗b , если угол между ними равен 60⁰, а модули равны 2 и 3 соответственно.

2.      Найдите скалярное произведение векторов ⃗a  и ⃗b, если угол между ними равен 45⁰, а модули

равны 3 и 2√2 соответственно.

3.      Найдите скалярное произведение векторов ⃗a  и ⃗b , если угол между ними равен 90⁰, а модули

равны 4 и 2√2 соответственно

4.      Найдите скалярно произведение векторов, если |⃗a | = 3, |⃗b | = 2 и угол между ними составляет 60⁰

5.      Найдите скалярное произведение векторов, если |⃗a | = 6, |⃗b | = √2 и угол между векторами составляет 30⁰

6.      Вычислите скалярное произведение векторов, если  и угол между векторами равен 45⁰

7.      Найдите скалярное произведение векторов, если , а угол между векторами составляет 240⁰

8.      Найдите скалярное произведение векторов, если |⃗a | = 6, |⃗b | = 2√2 и угол между векторами равен 135⁰

9.      Найдите скалярное произведение векторов, если |⃗a | = 3, |⃗b | = 2√2 и угол между векторами равен 270⁰

10.  Найдите скалярное произведение векторов, если |⃗a | = 5, |⃗b | = 4, а угол между векторами составляет 120⁰